MY-ASSIGNMENTEXPERT™可以为您提供sydney DATA5711 Bayesian Analysis贝叶斯分析课程的代写代考和辅导服务!
这是悉尼大学贝叶斯分析课程的代写成功案例。

DATA5711课程简介
Increased computing power has meant that many Bayesian methods can now be easily implemented and provide solutions to problems that have previously been intractable. Bayesian methods allow researchers to incorporate prior knowledge into their statistical models. This unit is made up of three distinct modules, each focusing on a different niche in the application of Bayesian statistical methods to complex data in, for example, geophysics, ecology and hydrology. These include (but are not restricted to) Bayesian methods and models; statistical inversion; approximate Bayesian inference for semiparametric regression. Across all modules you will develop expertise in Bayesian computational statistics. On completion of this unit you will be able to apply appropriate Bayesian methods to a variety of applications in science, and other data-heavy disciplines to develop a better understanding of the information inherent in complex datasets.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. Demonstrate a coherent and advanced understanding of key concepts in computational statistics.
- LO2. Apply fundamental principles and results in statistics to solve given problems.
- LO3. Distinguish and compare the properties of different types of statistical models and statistical methods applicable to them.
- LO4. Identify assumptions required for various statistical methods to be valid and devise methods for testing these assumptions.
- LO5. Devise statistical solutions to complex problems.
- LO6. Adapt various computational techniques to build software for solving particular statistical problems.
- LO7. Communicate coherent statistical arguments appropriately to student and expert audiences, both orally and through written work.
DATA5711 Bayesian Analysis HELP(EXAM HELP, ONLINE TUTOR)
You are visiting a town with buses whose licence plates show their numbers consecutively from 1 up to however many there are. In your mind the number of buses could be anything from one to five, with all possibilities equally likely.
Whilst touring the town you first happen to see Bus 3 .
Assuming that at any point in time you are equally likely to see any of the buses in the town, how likely is it that the town has at least four buses?
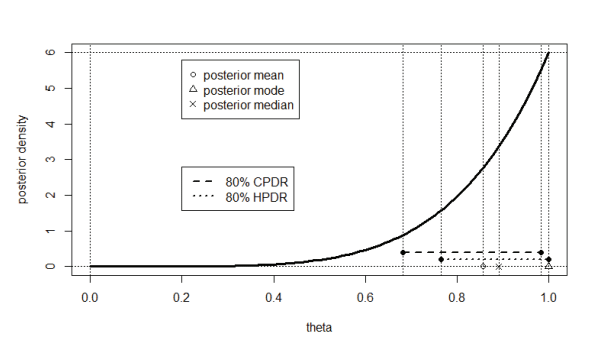
Let $\theta$ be the number of buses in the town and let $y$ be the number of the bus that you happen to first see. Then an appropriate Bayesian model is:
$$
\begin{aligned}
& f(y \mid \theta)=1 / \theta, y=1, \ldots, \theta \
& f(\theta)=1 / 5, \theta=1, \ldots, 5 \quad \text { (prior). }
\end{aligned}
$$
Note: We could also write this model as:
$$
\begin{aligned}
& (y \mid \theta) \sim D U(1, \ldots, \theta) \
& \theta \sim D U(1, \ldots, 5),
\end{aligned}
$$
where $D U$ denotes the discrete uniform distribution. (See Appendix B.9 for details regarding this distribution. Appendix B also provides details regarding some other important distributions that feature in this book.)
So the posterior density of $\theta$ is
$$
\begin{aligned}
f(\theta \mid y) & \propto f(\theta) f(y \mid \theta) \
& \propto 1 \times 1 / \theta, \quad \theta=y, \ldots, 5 .
\end{aligned}
$$
Noting that $y=3$, we have that
$$
f(\theta \mid y) \propto\left{\begin{array}{l}
1 / 3, \theta=3 \
1 / 4, \theta=4 \
1 / 5, \theta=5
\end{array}\right.
$$
Now, $1 / 3+1 / 4+1 / 5=(20+15+12) / 60=47 / 60$, and so
$$
f(\theta \mid y)=\left{\begin{array}{l}
\frac{1 / 3}{47 / 60}=\frac{20}{47}, \theta=3 \
\frac{1 / 4}{47 / 60}=\frac{15}{47}, \theta=4 \
\frac{1 / 5}{47 / 60}=\frac{12}{47}, \theta=5 .
\end{array}\right.
$$
So the posterior probability that the town has at least four buses is
$$
\begin{aligned}
P(\theta \geq 4 \mid y) & =\sum_{\theta: \theta \geq 4} f(\theta \mid y)=f(\theta=4 \mid y)+f(\theta=5 \mid y) \
& =1-f(\theta=3 \mid y)=1-\frac{20}{47}=\frac{27}{47}=0.5745 .
\end{aligned}
$$
In each of nine indistinguishable boxes there are nine balls, the $i$ th box having $i$ red balls and $9-i$ white balls $(i=1, \ldots, 9)$.
One box is selected randomly from the nine, and then three balls are chosen randomly from the selected box (without replacement and without looking at the remaining balls in the box).
Exactly two of the three chosen balls are red. Find the probability that the selected box has at least four red balls remaining in it.
Let: $\quad N=$ the number of balls in each box (9)
$n=$ the number of balls chosen from the selected box (3)
$\theta=$ the number of red balls initially in the selected box $(1,2, \ldots, 8$ or 9$)$
$y=$ the number of red balls amongst the $n$ chosen balls (2).
Then an appropriate Bayesian model is:
$(y \mid \theta) \sim \operatorname{Hyp}(N, \theta, n) \quad$ (Hypergeometric with parameters
$N, \theta$ and $n$, and having mean $n \theta / N$ )
$\theta \sim D U(1, \ldots, N) \quad$ (discrete uniform over the integers $1,2, \ldots, N$ ).
For this model, the posterior density of $\theta$ is
$$
\begin{aligned}
f(\theta \mid y) & \propto f(\theta) f(y \mid \theta)=\frac{1}{N} \times\left(\begin{array}{l}
\theta \
y
\end{array}\right)\left(\begin{array}{c}
N-\theta \
n-y
\end{array}\right) /\left(\begin{array}{l}
N \
n
\end{array}\right) \
& \propto \frac{\theta !(N-\theta) !}{(\theta-y) !(N-\theta-(n-y)) !}, \quad \theta=y, \ldots, N-(n-y) .
\end{aligned}
$$
In our case,
$$
f(\theta \mid y) \propto \frac{\theta !(9-\theta) !}{(\theta-2) !(9-\theta-(3-2)) !}, \theta=2, \ldots, 9-(3-2),
$$
or more simply,
$$
f(\theta \mid y) \propto \theta(\theta-1)(9-\theta), \quad \theta=2, \ldots, 8 .
$$
Thus $f(\theta \mid y) \propto\left{\begin{array}{l}14, \theta=2 \ 36, \theta=3 \ 60, \theta=4 \ 80, \theta=5 \ 90, \theta=6 \ 84, \theta=7 \ 56, \theta=8\end{array}\right} \equiv k(\theta)$,
where
$$
c \equiv \sum_{\theta=1}^8 k(\theta)=14+36+\ldots+56=420 .
$$
So $f(\theta \mid y)=\frac{k(\theta)}{c}=\left{\begin{array}{l}14 / 420=0.03333, \theta=2 \ 36 / 420=0.08571, \theta=3 \ 60 / 420=0.14286, \theta=4 \ 80 / 420=0.19048, \theta=5 \ 90 / 420=0.21429, \theta=6 \ 84 / 420=0.20000, \theta=7 \ 56 / 420=0.13333, \theta=8 .\end{array}\right.$
The probability that the selected box has at least four red balls remaining is the posterior probability that $\theta$ (the number of red balls initially in the box) is at least 6 (since two red balls have already been taken out of the box). So the required probability is
$$
P(\theta \geq 6 \mid y)=\frac{90+84+56}{420}=\frac{23}{42}=0.5476 .
$$
Consider the following Bayesian model:
$$
\begin{aligned}
& (y \mid \theta) \sim \operatorname{Binomial}(n, \theta) \
& \theta \sim \operatorname{Beta}(\alpha, \beta) \quad \text { (prior). }
\end{aligned}
$$
Find the posterior distribution of $\theta$.
The posterior density is
$$
\begin{aligned}
f(\theta \mid y) & \propto f(\theta) f(y \mid \theta) \
& =\frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)} \times\left(\begin{array}{c}
n \
y
\end{array}\right) \theta^y(1-\theta)^{n-y} \
& \propto \theta^{\alpha-1}(1-\theta)^{\beta-1} \times \theta^y(1-\theta)^{n-y} \quad \text { (ignoring constants which } \
& =\theta^{(\alpha+y)-1}(1-\theta)^{(\beta+n-y)-1}, 0<\theta<1 .
\end{aligned}
$$
This is the kernel of the beta density with parameters $\alpha+y$ and $\beta+n-y$. It follows that the posterior distribution of $\theta$ is given by
$$
(\theta \mid y) \sim \operatorname{Beta}(\alpha+y, \beta+n-y)
$$
and the posterior density of $\theta$ is (exactly)
$$
f(\theta \mid y)=\frac{\theta^{(\alpha+y)-1}(1-\theta)^{(\beta+n-y)-1}}{B(\alpha+y, \beta+n-y)}, 0<\theta<1 .
$$
For example, suppose that $\alpha=\beta=1$, that is, $\theta \sim \operatorname{Beta}(1,1)$.
Then the prior density is $f(\theta)=\frac{\theta^{1-1}(1-\theta)^{1-1}}{B(1,1)}=1,0<\theta<1$.
Thus the prior may also be expressed by writing $\theta \sim U(0,1)$.
For example, suppose that $\alpha=\beta=1$, that is, $\theta \sim \operatorname{Beta}(1,1)$.
Then the prior density is $f(\theta)=\frac{\theta^{1-1}(1-\theta)^{1-1}}{B(1,1)}=1,0<\theta<1$.
Thus the prior may also be expressed by writing $\theta \sim U(0,1)$.
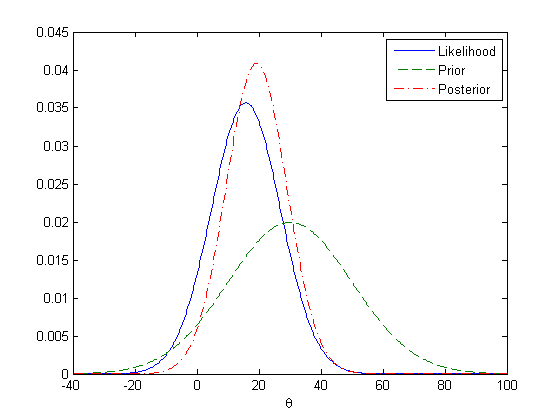
Also, suppose that $n=2$. Then there are three possible values of $y$, namely 0,1 and 2, and these lead to the following three posteriors, respectively:
$$
\begin{aligned}
& (\theta \mid y) \sim \operatorname{Beta}(1+0,1+2-0)=\operatorname{Beta}(1,3) \
& (\theta \mid y) \sim \operatorname{Beta}(1+1,1+2-1)=\operatorname{Beta}(2,2) \
& (\theta \mid y) \sim \operatorname{Beta}(1+2,1+2-2)=\operatorname{Beta}(3,1) .
\end{aligned}
$$
These three posteriors and the prior are illustrated in Figure 1.5.

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY DATA5711 BAYESIAN ANALYSIS贝叶斯分析课程的代写代考和辅导服务!