MY-ASSIGNMENTEXPERT™可以为您提供 torontomu ECN614 Game theory博弈论的代写代考和辅导服务!
这是怀雅逊大学博弈论课程的代写成功案例。
ECN614课程简介
Game theory studies the interactions and conflicts between decision-making agents. This course focuses on its application to economic issues such as market structure, auctions and bargaining. It begins by introducing the concepts of action, strategies, cooperation and non-cooperation, and equilibrium. The assumption of complete information is then relaxed and the application of game theory to situations of incomplete and imperfect information is explored. The course draws on real world examples to illustrate core concepts, such as the Prisoner’s Dilemma and buying votes. These examples borrow from micro, macro and experimental economics.
Prerequisites
Game theory is the study of mathematical models of strategic interactions among rational agents.It has applications in all fields of social science, as well as in logic, systems science and computer science. The concepts of game theory are used extensively in economics as well. The traditional methods of game theory addressed two-person zero-sum games, in which each participant’s gains or losses are exactly balanced by the losses and gains of other participants. In the 21st century, the advanced game theories apply to a wider range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers.
ECN614 Game theory HELP(EXAM HELP, ONLINE TUTOR)
Consider a version of the Cournot duopoly game, which will be thoroughly analyzed in Chapter 10. Two firms (1 and 2) compete in a homogeneous goods market, where the firms produce exactly the same good. The firms simultaneously and independently select quantities to produce. The quantity selected by firm $i$ is denoted $q_i$ and must be greater than or equal to zero, for $i=1,2$. The market price is given by $p=2-q_1-q_2$. For simplicity, assume that the cost to firm $i$ of producing any quantity is zero. Further, assume that each firm’s payoff is defined as its profit. That is, firm $i$ ‘s payoff is $p q_i$, where $j$ denotes firm $i$ ‘s opponent in the game. Describe the normal form of this game by expressing the strategy spaces and writing the payoffs as functions of the strategies.
The normal form specifies players, strategy spaces, and payoff functions. Here there are two players, so $n=2$, and $S_1=S_2=[0, \infty)$. The payoff to player $i$ is given by $u_i\left(q_i, q_j\right)=\left(2-q_i-q_j\right) q_i$, for $i=1,2$ and $j$ denoting the other player.
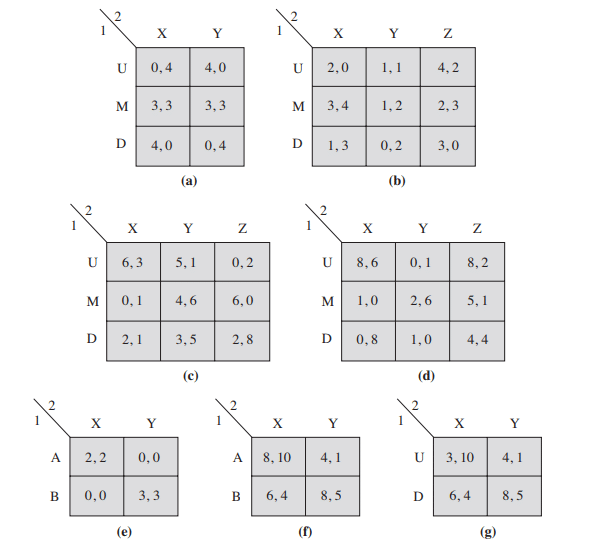
Evaluate the following payoffs for the game given by the normal form pictured here. [Remember, a mixed strategy for player 1 is $\sigma_1 \in \Delta{\mathrm{U}, \mathrm{M}, \mathrm{D}}$, where $\sigma_1(\mathrm{U})$ is the probability that player 1 plays strategy $\mathrm{U}$, and so forth. For simplicity, we write $\sigma_1$ as $\left(\sigma_1(\mathrm{U}), \sigma_1(\mathrm{M}), \sigma_1(\mathrm{D})\right)$, and similarly for player 2.]
\begin{tabular}{c|c|c|c|}
\hline$U$ & \multicolumn{1}{c}{} \
\cline { 2 – 4 } & 10,0 & 0,10 & 3,3 \
& 2,10 & 10,2 & 6,4 \
\cline { 2 – 4 } $\mathrm{D}$ & 3,3 & 4,6 & 6,6 \
\hline
\end{tabular}
(a) $u_1(\mathrm{U}, \mathrm{C})$
(b) $u_2(\mathrm{M}, \mathrm{R})$
(c) $u_2(\mathrm{D}, \mathrm{C})$
(d) $u_1\left(\sigma_1, \mathrm{C}\right)$ for $\sigma_1=(1 / 3,2 / 3,0)$
(e) $u_1\left(\sigma_1, \mathrm{R}\right)$ for $\sigma_1=(1 / 4,1 / 2,1 / 4)$
(f) $u_1\left(\sigma_1, \mathrm{~L}\right)$ for $\sigma_1=(0,1,0)$
(g) $u_2\left(\sigma_1\right.$, R) for $\sigma_1=(1 / 3,2 / 3,0)$
(h) $u_2\left(\sigma_1, \sigma_2\right)$ for $\sigma_1=(1 / 2,1 / 2,0)$ and $\sigma_2=(1 / 4,1 / 4,1 / 2)$.
(a) $u_1(\mathrm{U}, \mathrm{C})=0$.
(b) $u_2(\mathrm{M}, \mathrm{R})=4$.
(c) $u_2(\mathrm{D}, \mathrm{C})=6$
(d) For $\sigma_1=(1 / 3,2 / 3,0), u_1\left(\sigma_1, \mathrm{C}\right)=(0) 1 / 3+(10) 2 / 3+0=20 / 3$.
(e) $u_1\left(\sigma_1, \mathrm{R}\right)=3(1 / 4)+6(1 / 2)+6(1 / 4)=21 / 4$.
(f) $u_1\left(\sigma_1, \mathrm{~L}\right)=2$.
(g) $u_2\left(\sigma_1, \mathrm{R}\right)=3(1 / 3)+4(2 / 3)+6(0)=11 / 3$.
(h)
$$
\begin{aligned}
& u_2\left(\sigma_1, \sigma_2\right)=0(1 / 2)(1 / 4)+10(1 / 2)(1 / 4)+3(1 / 2)(1 / 2)+ \
& 10(1 / 2)(1 / 4)+2(1 / 2)(1 / 4)+4(1 / 2)(1 / 2)+3(0)(1 / 4)+ \
& 6(0)(1 / 4)+6(0)(1 / 2)=9 / 2
\end{aligned}
$$
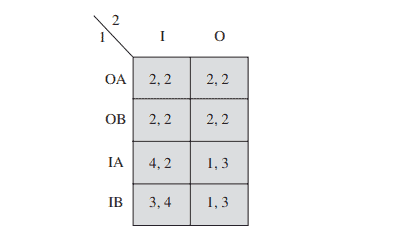
Evaluate the following payoffs for the game pictured here:
(a) $u_1\left(\sigma_1\right.$, I) for $\sigma_1=(1 / 4,1 / 4,1 / 4,1 / 4)$
(b) $u_2\left(\sigma_1, \mathrm{O}\right)$ for $\sigma_1=(1 / 8,1 / 4,1 / 4,3 / 8)$
(c) $u_1\left(\sigma_1, \sigma_2\right)$ for $\sigma_1=(1 / 4,1 / 4,1 / 4,1 / 4), \sigma_2=(1 / 3,2 / 3)$
(d) $u_1\left(\sigma_1, \sigma_2\right)$ for $\sigma_1=(0,1 / 3,1 / 6,1 / 2), \sigma_2=(2 / 3,1 / 3)$
(a) $u_1\left(\sigma_1, \mathrm{I}\right)=2(1 / 4)+2(1 / 4)+4(1 / 4)+3(1 / 4)=11 / 4$.
(b) $u_2\left(\sigma_1, \mathrm{O}\right)=21 / 8$.
(c)
$$
\begin{aligned}
& u_1\left(\sigma_1, \sigma_2\right)=2(1 / 4)+2(1 / 4)+4(1 / 4)(1 / 3)+(1 / 4)(2 / 3)+ \
& (3 / 4)(1 / 3)+14(2 / 3)=23 / 12
\end{aligned}
$$
(d) $u_1\left(\sigma_1, \sigma_2\right)=7 / 3$.
Consider a version of the Cournot duopoly game, where firms 1 and 2 simultaneously and independently select quantities to produce in a market. The quantity selected by firm $i$ is denoted $q_i$ and must be greater than or equal to zero, for $i=1,2$. The market price is given by $p=100-2 q_1-2 q_2$. Suppose that each firm produces at a cost of 20 per unit. Further, assume that each firm’s payoff is defined as its profit. (If you completed Exercise 5 of Chapter 3, then you have already dealt with this type of game.) Suppose that player 1 has the belief that player 2 is equally likely to select each of the quantities 6,11 , and 13. What is player l’s expected payoff of choosing a quantity of 14 ?
(a) $B R_1\left(\theta_2\right)={\mathrm{P}}$.
(b) $B R_1\left(\theta_2\right)={\mathrm{R}, \mathrm{S}}$.
(c) $B R_1\left(\theta_2\right)={\mathrm{P}}$.
(d) $B R_1\left(\theta_2\right)={\mathrm{R}, \mathrm{P}, \mathrm{S}}$.
MY-ASSIGNMENTEXPERT™可以为您提供 TORONTOMU ECN614 GAME THEORY博弈论的代写代考和辅导服务!