MY-ASSIGNMENTEXPERT™可以为您提供utasKMA255 Operations research运筹学的代写代考和辅导服务!
这是塔斯马尼亚大学 运筹学的代写成功案例。
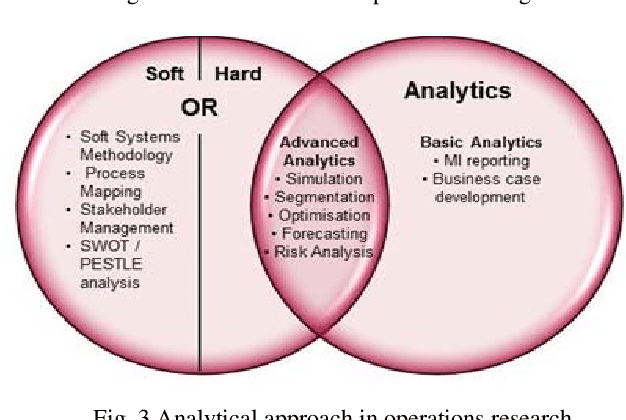
KMA255课程简介
This unit teaches students skills and techniques that are used to answer practical questions arising in Operations Research. These questions typically also arise in Engineering, Management, Finance, Economics, and Teaching. For example, How long do I expect to have to wait for the next bus? How should I balance the products my factory makes, to maximise my profit? and What is the best way to send electricity from this set of power stations to these homes, to minimise power loss?
Operations Research includes the solution of optimization problems, modelling, and simulation. This unit provides necessary background in probability and graph theory, and then using those tools introduces students to methods in modelling stochastic systems as Discrete Time Markov Chains, and analysing their expected behaviour. It also gives students tools, such as the Simplex Method, to solve Linear Programming optimization and Transportation problems, and heuristic methods to solve computationally intractable problems like the Travelling Salesman Problem.
This unit is a required component of the Statistics and Decision Science major in the BSc.
Prerequisites
- Explain and apply fundamentals of probability and graph theory relevant to operations research.
- Analyse short- and long- term behaviour of discrete time Markov chains.
- Solve problems in linear programming using standard techniques.
- Select and apply standard heuristic methods to computationally intractable problems in operations research.
- Interpret and communicate mathematical arguments using appropriate terminology and notation, as they relate to problems in operations research.
KMA255 Operations research HELP(EXAM HELP, ONLINE TUTOR)
Consider a noisy target $y=\mathbf{w}f^T \mathbf{x}+\epsilon$, where $\mathbf{x} \in \mathbb{R}^{d+1}$ (including the added coordinate $x_0=1$ ), $y \in \mathbb{R}, \mathbf{w}_f \in \mathbb{R}^{d+1}$ is an unknown vector, and $\epsilon$ is an i.i.d. noise term with zero mean and $\sigma^2$ variance. Assume that we run linear regression on a training data set $\mathcal{D}=\left{\left(\mathbf{x}_1, y_1\right), \ldots,\left(\mathbf{x}_N, y_N\right)\right}$ generated i.i.d. from some $P(\mathbf{x})$ and the noise process above, and obtain the weight vector $\mathbf{w}{\text {lin }}$. As briefly discussed in Lecture 9 , it can be shown that the expected in-sample error $E_{\text {in }}\left(\mathbf{w}{\text {lin }}\right)$ with respect to $\mathcal{D}$ is given by: $$ \mathbb{E}{\mathcal{D}}\left[E_{\mathrm{in}}\left(\mathbf{w}{\mathrm{lin}}\right)\right]=\sigma^2\left(1-\frac{d+1}{N}\right) . $$ For $\sigma=0.1$ and $d=11$, what is the smallest number of examples $N$ such that $\mathbb{E}{\mathcal{D}}\left[E_{\text {in }}\left(\mathbf{w}_{\operatorname{lin}}\right)\right]$ is no less than 0.006 ? Choose the correct answer; explain your answer.
[a] 25
[b] 30
[c] 35
[d] 40
[e] 45
As shown in Lecture 9 , minimizing $E_{\text {in }}(\mathbf{w})$ for linear regression means solving $\nabla E_{\text {in }}(\mathbf{w})=0$, which in term means solving the so-called normal equation
$$
\mathrm{X}^T \mathrm{X} \mathbf{w}=\mathrm{X}^T \mathbf{y}
$$
Which of the following statement about the normal equation is correct for any features $\mathrm{X}$ and labels $\mathbf{y}$ ? Choose the correct answer; explain your answer.
[a] There exists at least one solution for the normal equation.
[b] If there exists a solution for the normal equation, $E_{\text {in }}(\mathbf{w})=0$ at such a solution.
[c] If there exists a unique solution for the normal equation, $E_{\text {in }}(\mathbf{w})=0$ at the solution.
[d] If $E_{\mathrm{in}}(\mathbf{w})=0$ at some $\mathbf{w}$, there exists a unique solution for the normal equation.
[e] none of the other choices
In Lecture 9, we introduced the hat matrix $\mathrm{H}=\mathrm{XX}^{\dagger}$ for linear regression. The matrix projects the label vector $\mathbf{y}$ to the “predicted” vector $\hat{\mathbf{y}}=\mathrm{Hy}$ and helps us analyze the error of linear regression. Assume that $\mathrm{X}^T \mathrm{X}$ is invertible, which makes $\mathrm{H}=\mathrm{X}\left(\mathrm{X}^T \mathrm{X}\right)^{-1} \mathrm{X}^T$. Now, consider the following operations on $\mathrm{X}$. Which operation can possibly change $\mathrm{H}$ ? Choose the correct answer; explain your answer.
[a] multiplying the whole matrix $\mathrm{X}$ by 2 (which is equivalent to scaling all input vectors by 2)
[b] multiplying each of the $i$-th column of $\mathrm{X}$ by $i$ (which is equivalent to scaling the $i$-th feature by $i)$
[c] multiplying each of the $n$-th row of $\mathrm{X}$ by $\frac{1}{n}$ (which is equivalent to scaling the $n$-th example by $\left.\frac{1}{n}\right)$
[d] adding three randomly-chosen columns $i, j, k$ to column 1 of $\mathrm{X}$
$$
\text { (i.e., } x_{n, 1} \leftarrow x_{n, 1}+x_{n, i}+x_{n, j}+x_{n, k} \text { ) }
$$
[e] none of the other choices (i.e. all other choices are guaranteed to keep H unchanged.)
Consider a coin with an unknown head probability $\theta$. Independently flip this coin $N$ times to get $y_1, y_2, \ldots, y_N$, where $y_n=1$ if the $n$-th flipping results in head, and 0 otherwise. Define $\nu=\frac{1}{N} \sum_{n=1}^N y_n$. How many of the following statements about $\nu$ are true? Choose the correct answer; explain your answer by illustrating why those statements are true.
- $\operatorname{Pr}(|\nu-\theta|>\epsilon) \leq 2 \exp \left(-2 \epsilon^2 N\right)$ for all $N \in \mathbb{N}$ and $\epsilon>0$.
- $\nu$ maximizes likelihood $(\hat{\theta})$ over all $\hat{\theta} \in[0,1]$.
- $\nu$ minimizes $E_{\text {in }}(\hat{y})=\frac{1}{N} \sum_{n=1}^N\left(\hat{y}-y_n\right)^2$ over all $\hat{y} \in \mathbb{R}$.
- $2 \cdot \nu$ is the negative gradient direction $-\nabla E_{\mathrm{in}}(\hat{y})$ at $\hat{y}=0$.
(Note: $\theta$ is similar to the role of the “target function” and $\hat{\theta}$ is similar to the role of the “hypothesis” in our machine learning framework.)
[a] 0
[b] 1
[c] 2
[d] 3
[e] 4
MY-ASSIGNMENTEXPERT™可以为您提供utasKMA255 Operations research运筹学的代写代考和辅导服务!





