MY-ASSIGNMENTEXPERT™可以为您提供my.uq.edu PHYS4040 Quantum field theory量子场论课程的代写代考和辅导服务!
这是昆士兰大学 量子场论课程的代写成功案例。
PHYS4040课程简介
Course Description: This course covers advanced topics from single-particle quantum mechanics, such as advanced quantum dynamics, path-integrals, and quantum decoherence. It will also cover introductory non-relativistic many-body quantum theory, relativistic quantum mechanics, and relativistic quantum field theory. We will look at selected applications from atom optics, condensed matter physics, and particle physics.
Assumed Background:
Students should have a sound understanding of quantum physics at the level of PHYS3040 (or equivalent). Background in special relativity (e.g. PHYS2100), electromagnetic fields (e.g. PHYS3051), condensed matter physics (e.g. PHYS2020) and statistical mechanics (e.g. PHYS3020) is strongly recommended.
Prerequisites
This course aims at a first introduction to relativistic quantum field theory. This plays a fundamental role in our understanding of particle physics but arises also in the study of statistical mechanics and second quantised condensed matter systems.
Course Changes in Response to Previous Student Feedback
The course has been modified to be more interactive, with more chance for students to work through problems with assistance.
PHYS4040 Quantum field theory HELP(EXAM HELP, ONLINE TUTOR)
Derive the transformations $x \rightarrow \frac{x+v t}{\sqrt{1-v^2}}$ and $t \rightarrow \frac{t+v x}{\sqrt{1-v^2}}$ in perturbation theory. Start with the Galilean transformation $x \rightarrow x+v t$. Add a transformation $t \rightarrow t+\delta t$ and solve for $\delta t$ assuming it is linear in $x$ and $t$ and preserves $t^2-x^2$ to $\mathcal{O}\left(v^2\right)$. Repeat for $\delta t$ and $\delta x$ to second order in $v$ and show that the result agrees with the second-order expansion of the full transformations.
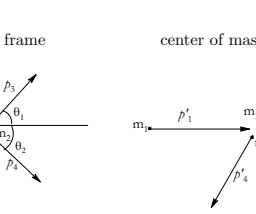
Special relativity and colliders.
(a) The Large Hadron Collider was designed to collide protons together at $14 \mathrm{TeV}$ center-of-mass energy. How many kilometers per hour less than the speed of light are the protons moving?
(b) How fast is one proton moving with respect to the other?
The GZK bound. In 1966 Greisen, Zatsepin and Kuzmin argued that we should not see cosmic rays (high-energy protons hitting the atmosphere from outer space) above a certain energy, due to interactions of these rays with the cosmic microwave background.
(a) The universe is a blackbody at $2.73 \mathrm{~K}$. What is the average energy of the photons in outer space (in electronvolts)?
(b) How much energy would a proton $\left(p^{+}\right)$need to collide with a photon $(\gamma)$ in outer space to convert it to a $135 \mathrm{MeV}$ pion $\left(\pi^0\right)$ ? That is, what is the energy threshold for $p^{+}+\gamma \rightarrow p^{+}+\pi^0$ ?
(c) How much energy does the outgoing proton have after this reaction?
This GZK bound was finally confirmed experimentally 40 years after it was conjectured [Abbasi et al., 2008].
Is the transformation $Y:(t, x, y, z) \rightarrow(t, x,-y, z)$ a Lorentz transformation? If so, why is it not considered with $P$ and $T$ as a discrete Lorentz transformation? If not, why not?
Compton scattering. Suppose we scatter an X-ray off an electron in a crystal, but we cannot measure the electron’s momentum, just the reflected X-ray momentum.
(a) Why is it OK to treat the electrons as free?
(b) Calculate the frequency dependence of the reflected X-ray on the scattering angle. Draw a rough plot.
(c) What happens to the distribution as you take the electron mass to zero?
(d) If you did not believe in quantized photon momenta, what kind of distribution might you have expected? [Hint: see [Compton, 1923].]

MY-ASSIGNMENTEXPERT™可以为您提供MY.UQ.EDU PHYS4040 QUANTUM FIELD THEORY量子场论课程的代写代考和辅导服务!