MY-ASSIGNMENTEXPERT™可以为您提供 torontomu ECN614 Game theory博弈论的代写代考和辅导服务!
这是怀雅逊大学博弈论课程的代写成功案例。
ECN614课程简介
Game theory studies the interactions and conflicts between decision-making agents. This course focuses on its application to economic issues such as market structure, auctions and bargaining. It begins by introducing the concepts of action, strategies, cooperation and non-cooperation, and equilibrium. The assumption of complete information is then relaxed and the application of game theory to situations of incomplete and imperfect information is explored. The course draws on real world examples to illustrate core concepts, such as the Prisoner’s Dilemma and buying votes. These examples borrow from micro, macro and experimental economics.
Prerequisites
Game theory is the study of mathematical models of strategic interactions among rational agents.It has applications in all fields of social science, as well as in logic, systems science and computer science. The concepts of game theory are used extensively in economics as well. The traditional methods of game theory addressed two-person zero-sum games, in which each participant’s gains or losses are exactly balanced by the losses and gains of other participants. In the 21st century, the advanced game theories apply to a wider range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers.
ECN614 Game theory HELP(EXAM HELP, ONLINE TUTOR)
Two medieval city-states, Simancas and Toro, are located near each other. Each city-state is controlled by a totalitarian prince, so each can be represented as a single player. Call the prince of Simancas player 1, and let the prince of Toro be called player 2 . The land surrounding each city-state can be divided among two uses: forested land for deer hunting, and cleared land for growing wheat. Each city-state has five units of land. At the outset, all of the land is forested.
Each city-state $i$ (where $i=1,2$ ) must make two decisions: how much land to clear for growing wheat, $g_i \in[0,5]$, and how many hounds to raise for hunting deer, $h_i \in[0, \infty)$. All decisions are made simultaneously.
Payoffs depend on the total quantity of forested land in both city-states (deer roam freely across borders) and the number of hounds raised in both city-states. The deer harvest for city-state $i$ is increasing in its own number of hounds but decreasing in the other city-state’s number of hounds. Specifically, the deer harvest in city-state $i$ is $\max \left{0,2 h_i-h_j\right}\left(10-g_i-g_j\right)$, where $j$ denotes the other city-state. Here, the “maximum” operator is needed to ensure that the harvest is never negative. The wheat-growing results for each city-state, on the other hand, depend only on its own quantity of cleared land. Specifically, the wheat harvest in city-state $i$ is $6 g_i$. Raising hounds and clearing land are both costly. Suppose the cost to citystate $i$ is $g_i^2+2 h_i^2$. Summing up, the payoff for city-state 1 is
$$
u_1\left(g_1, h_1, g_2, h_2\right)=\max \left{0,2 h_1-h_2\right}\left(10-g_1-g_2\right)+6 g_1-g_1^2-2 h_1^2 \text {, }
$$
and the payoff for city-state 2 is
$$
u_2\left(g_1, h_1, g_2, h_2\right)=\max \left{0,2 h_2-h_1\right}\left(10-g_2-g_1\right)+6 g_2-g_2^2-2 h_2^2 \text {. }
$$
(a) Show that the strategy $\left(g_i, h_i\right)=(0,0)$ is dominated for each city-state $i$.
(b) Show that any strategy with $h_i>5$ is dominated for each city-state $i$.
(c) Show that $\left(g_1, h_1\right)=\left(g_2, h_2\right)=(1,4)$ is not efficient.
(a) The strategy $\left(g_i, h_i\right)=(0,0)$ yields a payoff of $u_i=0$ regardless of what the other player does. It is dominated by the strategy $\left(g_i, h_i\right)=(1,0)$, which always yields a payoff of $u_i=6 \cdot 1-1^2=5$.
(b) Any strategy $\left(g_i, h_i\right)$ with $h_i>5$ is dominated by the strategy $\left(g_i, 5\right)$ : The difference in payoffs between them, for any strategy of player $-i$, is
$$
\begin{aligned}
& u_i\left(g_i, 5, g_{-i}, h_{-i}\right)-u_i\left(g_i, h_i, g_{-i}, h_{-i}\right) \
& =\left(\max \left{0,10-h_{-i}\right}-\max \left{0,2 h_i-h_{-i}\right}\right) \sum_{j=S, T}\left(5-g_j\right)-50+2 h_i^2,
\end{aligned}
$$
which is strictly less than zero since $2 h_i>10$ and $2 h_i^2>50$.
(c) If $\left(g_1, h_1\right)=\left(g_2, h_2\right)=(1,4)$, then
$$
u_1=u_2=(2 \cdot 4-4)(10-1-1)+6 \cdot 1-1^2-2 \cdot 4^2=5 \text {, }
$$
where as the city-states could instead play $\left(g_1^{\prime}, h_1^{\prime}\right)=\left(g_2^{\prime}, h_2^{\prime}\right)=(3,2)$ to attain
$$
u_1=u_2=(2 \cdot 2-2)(10-3-3)+6 \cdot 3-3^2-2 \cdot 2^2=9 .
$$
Hence $\left(g_1^{\prime}, h_1^{\prime}\right)=\left(g_2^{\prime}, h_2^{\prime}\right)=(3,2)$ is more efficient than $\left(g_1, h_1\right)=$ $\left(g_2, h_2\right)=(1,4)$.
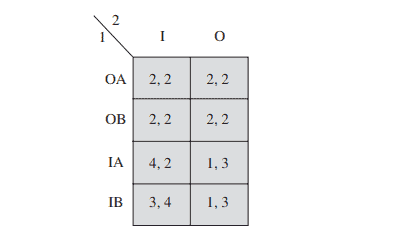
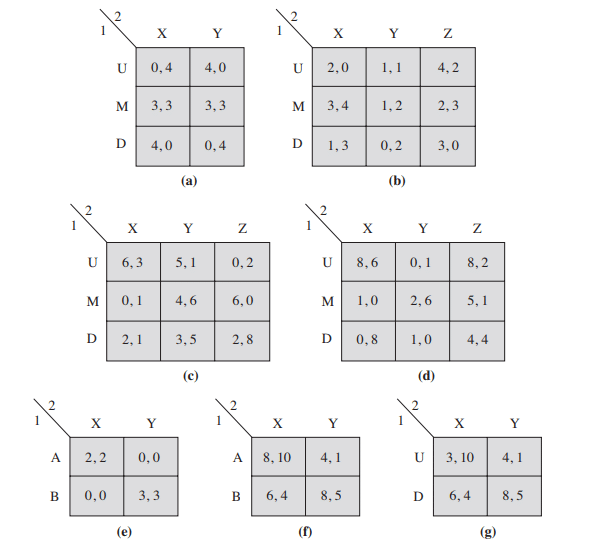
Determine the set of rationalizable strategies for each of the following games.
(a) $R={\mathrm{U}, \mathrm{M}, \mathrm{D}} \times{\mathrm{X}, \mathrm{Y}}$.
(b) $\mathrm{U}$ dominates $\mathrm{D}$. When $\mathrm{D}$ is ruled out, $\mathrm{Z}$ dominates $\mathrm{Y}$. Thus, $R={\mathrm{U}, \mathrm{M}} \times{\mathrm{X}, \mathrm{Z}}$.
(c) $R={(\mathrm{U}, \mathrm{X})}$.
(d) $R={\mathrm{U}, \mathrm{M}} \times{\mathrm{X}, \mathrm{Y}}$.
(e) $R={\mathrm{A}, \mathrm{B}} \times{\mathrm{X}, \mathrm{Y}}$.
(f) $R={\mathrm{A}, \mathrm{B}} \times{\mathrm{X}, \mathrm{Y}}$.
(g) $R={(\mathrm{D}, \mathrm{Y})}$.
Suppose that in some two-player game, $s_1$ is a rationalizable strategy for player 1. If $s_2$ is a best response to $s_1$, is $s_2$ a rationalizable strategy for player 2? Explain.
Yes. If $s_1$ is rationalizable, then $s_2$ is a best response to a strategy of player 1 that may rationally be played. Thus, player 2 can rationalize strategy $s_2$.
Consider our nine-region location game to be a model of competition between two political candidates. Fifty voters are located in each of the nine regions of the political spectrum; each voter will vote for the closest candidate. Voters in regions equidistant from the two candidates will split evenly between them.
(a) Assume that each candidate wants to maximize the number of votes he or she receives. Are the candidates’ preferences the same as those modeled in the basic location game? Discuss how this setting differs from the setting in which candidates want to maximize the probability of winning (with the rule that the candidate with the most votes wins the election and, in case of a tie, each candidate is awarded the office with probability $1 / 2$ ).
(b) Suppose, contrary to the basic location model, that voters are not uniformly distributed across the nine regions. Instead, whereas regions $1,2,3,4,5,8$, and 9 each contains fifty voters, regions 6 and 7 each contains $x$ voters. Analyze the candidate location game for the case in which $x=75$. In a rationalizable outcome, can one of the candidates win with probability 1 ?
(c) What happens if $x>75$ or $x<75$ ?
(a) Yes, preferences are as modeled in the basic location game. However, if each player’s objective is to maximize his or her probability of winning, the best responses are a bit different. For example, $B R_1(1)={2,3,4, \ldots, 8}$ because all of these strategies give player 1 certain victory. In the basic location game, $B R_1(1)={2}$.
(b) $R={5,6} \times{5,6}$. Unlike in the basic location model, there is not a single region that is “in the middle.” Here, each of the rationalizable strategy profiles yields 250 to each candidate. No rationalizable profile leads one of the candidates to win with probability 1 .
(c) When $x>75, R={(6,6)}$. For intuition, note that player $i$ ‘s best response to 5 is 6 , and his or her best response to 6 is 6 . When $x<75, R={(5,5)}$.
MY-ASSIGNMENTEXPERT™可以为您提供 TORONTOMU ECN614 GAME THEORY博弈论的代写代考和辅导服务!