MY-ASSIGNMENTEXPERT™可以为您提供 torontomu ECN614 Game theory博弈论的代写代考和辅导服务!
这是怀雅逊大学博弈论课程的代写成功案例。

ECN614课程简介
Game theory studies the interactions and conflicts between decision-making agents. This course focuses on its application to economic issues such as market structure, auctions and bargaining. It begins by introducing the concepts of action, strategies, cooperation and non-cooperation, and equilibrium. The assumption of complete information is then relaxed and the application of game theory to situations of incomplete and imperfect information is explored. The course draws on real world examples to illustrate core concepts, such as the Prisoner’s Dilemma and buying votes. These examples borrow from micro, macro and experimental economics.
Prerequisites
Game theory is the study of mathematical models of strategic interactions among rational agents.It has applications in all fields of social science, as well as in logic, systems science and computer science. The concepts of game theory are used extensively in economics as well. The traditional methods of game theory addressed two-person zero-sum games, in which each participant’s gains or losses are exactly balanced by the losses and gains of other participants. In the 21st century, the advanced game theories apply to a wider range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers.
ECN614 Game theory HELP(EXAM HELP, ONLINE TUTOR)
Consider a duopoly game in which two firms simultaneously and independently select prices. Assume that the prices are required to be greater than or equal to zero. Denote firm 1’s price as $p_1$ and firm 2’s price as $p_2$. The firms’ products are differentiated. After the prices are set, consumers demand $10-p_1+p_2$ units of the good that firm 1 produces. Consumers demand $10-p_2+p_1$ units of the good that firm 2 produces. Assume that each firm must supply the number of units demanded. Also assume that each firm produces at zero cost. The payoff for each firm is equal to the firm’s profit.
(a) Write the payoff functions of the firms (as a function of their strategies $p_1$ and $p_2$ ).
(b) Compute firm 2’s best-response function (as a function of $p_1$ ).
(c) Can you determine the rationalizable strategies in this game by inspecting the graph of the best-response functions? What are the rationalizable strategies?
(a) $u_1\left(p_1, p_2\right)=\left(10-p_1+p_2\right) p_1 \cdot u_2\left(p_1, p_2\right)=\left(10-p_2+p_1\right) p_2$.
(b) We have $u_i\left(p_1, p_2\right)=10 p_i-p_i^2+p_j p_i$. We solve for $p_i$ that maximizes player $i$ ‘s payoff given $\bar{p}_j$, the expected value of $p_j$ according to player $i$ ‘s belief. The first-order condition yields $B R_i\left(\bar{p}_j\right)=5+\bar{p}_j / 2$.
(c) There is no upper bound on the price a player can select. Thus, we do not obtain a unique rationalizable strategy profile. The best-response functions are represented in the following diagram.
We have $R_i^1=[5, \infty)$ for $i=1,2$. Noting that $B R_i(5)=15 / 2$, we have $R_i^2=[15 / 2, \infty)$. Repeating the analysis yields $R_i=[10, \infty)$ for $i=1,2$.
Consider an industry in which two firms compete by simultaneously and independently selecting prices for their goods. Firm 1’s product and firm 2’s product are imperfect substitutes, so that an increase in one firm’s price will lead to an increase in the quantity demanded of the other firm’s product. In particular, each firm $i$ faces the following demand curve:
$$
q_i=\max \left{0,24-2 p_i+p_j\right}
$$
where $q_i$ is the quantity that firm $i$ sells, $p_i$ is firm $i$ ‘s price, and $p_j$ is the other firm’s price. (The “maximum” operator is needed to ensure that quantity demanded is never negative.)
Suppose that the maximum possible price is 20 and the minimum price is zero, so the strategy space for each firm $i$ is $S_i=[0,20]$. Both firms produce with no costs.
(a) What is firm $i$ ‘s profit as a function of the strategy profile $\left(p_1, p_2\right)$ ? Let each firm’s payoff be defined as its profit.
(b) Show that for each firm $i$, prices less than 6 and prices greater than 11 are dominated strategies, whereas prices from 6 to 11 are not dominated, so $B_i=[6,11]$.
(c) Consider a reduced game in which firms select prices between $x$ and $y$, where $x<y$. What strategies are undominated in such a game? Use your answer to compute the set of rationalizable strategies in the original game.
(a) $\pi_i\left(p_i, p_j\right)=\max \left{0,\left(24-2 p_i+p_j\right) p_i\right}$.
(b) Note that $\partial \pi_i / \partial p_i=24-4 p_i+p_j$ as long as profits are strictly positive. Because $p_j \geq 0$, both profits and this partial derivative are strictly positive whenever $p_i<6$. Thus, increasing $p_i$ in this range yields an increase in profits. Hence a price of 6 dominates all lower prices. Similarly, because $p_j \leq 20, \partial \pi_i / \partial p_i=24-4 p_i+p_j$ is always negative for $p_i>11$. Note that $\pi_i\left(11, p_j\right)=22+11 p_j$ so for any $p_j \in[0,20]$, choosing $p_i=11$ results in a nonnegative profit. So $p_i=11$ dominates all $p_i>11$. To see that $B_i=[6,11]$, consider player $i$ ‘s first-order condition for maximizing $\left(24-2 p_i+p_j\right) p_i$, which is $24-4 p_i+p_j=0$. We thus have $B R_i^*\left(\bar{p}_j\right)=6+\bar{p}_j / 4$, which runs from 6 to 11 as $\bar{p}_j$ goes from 0 to 20. This implies that $B_i=[6,11]$ for $i=1,2$.
(c) The analysis proceeds as in Exercise 5, but here there is an upper bound on strategies and so high prices are removed in the iterative procedure. The maximum and minimum values of $R_i^k$ converge to 8 as $k$ increases, so the only rationalizable strategy profile is $(8,8)$.
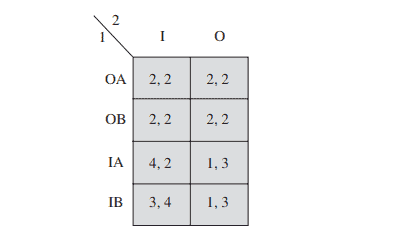
Consider the normal-form game pictured here.
(a) What are the Nash equilibria of this game?
(b) Which of these equilibria are efficient?
(c) Is the set $X={\mathrm{w}, \mathrm{x}} \times{\mathrm{b}, \mathrm{c}}$ weakly congruent?
(a) The Nash equilibria are (w, b) and (y, c).
(b) $(\mathrm{y}, \mathrm{c})$ is efficient.
(c) $X$ is not weakly congruous because strategy ” $\mathrm{a}$ ” is never a best response.
Find the Nash equilibrium of the following normal-form game: $S_1=[0,1], S_2=[0,1], u_1\left(s_1, s_2\right)=3 s_1-2 s_1 s_2-2 s_1^2$, and $u_2\left(s_1, s_2\right)=$ $s_2+2 s_1 s_2-2 s_2^2$. (The solution is interior, so you can use calculus.)
Player 1 chooses $s_1$ to maximize $3 s_1-2 s_1 s_2-2 s_1^2$. Differentiating with respect to $s_1$ yields the first-order condition $3-2 s_2-4 s_1=0$. Rearranging, we obtain player 1’s best-response function: $B R_1\left(\bar{s}_2\right)=3 / 4-\bar{s}_2 / 2$. Player 2 chooses $s_2$ to maximize $s_2+2 s_1 s_2-2 s_2^2$. Her best-response function is $B R_2\left(\bar{s}_1\right)=1 / 4+\bar{s}_1 / 2$. The Nash equilibrium is the strategy profile that solves the system of equations $s_1=3 / 4-s_2 / 2$ and $s_2=1 / 4+s_1 / 2$. This is $s^*=(1 / 2,1 / 2)$.
MY-ASSIGNMENTEXPERT™可以为您提供 TORONTOMU ECN614 GAME THEORY博弈论的代写代考和辅导服务!