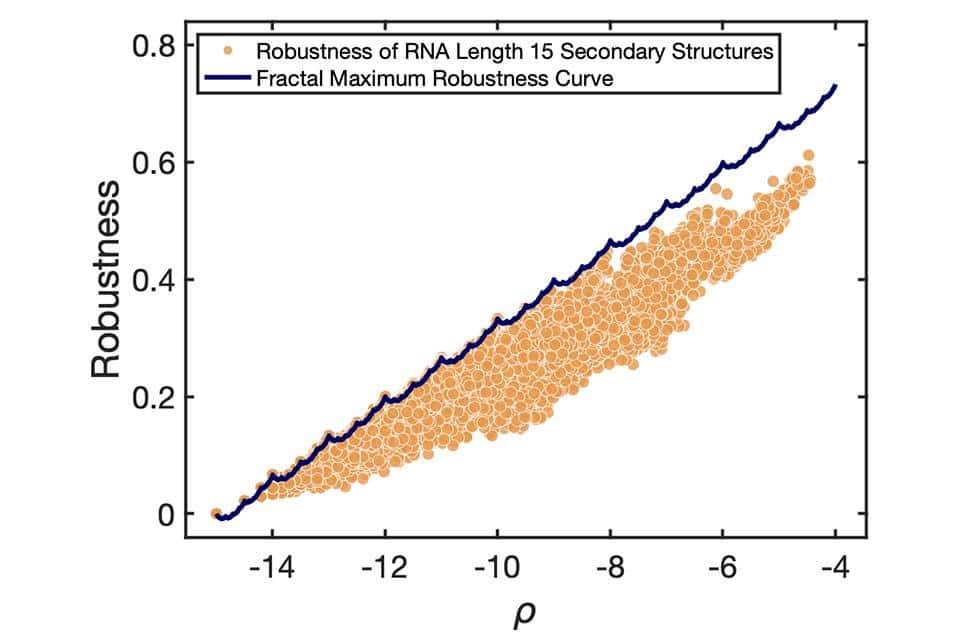
MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH2988 Number theory 数论的代写代考和辅导服务!
这是悉尼大学 数论课程的代写成功案例。
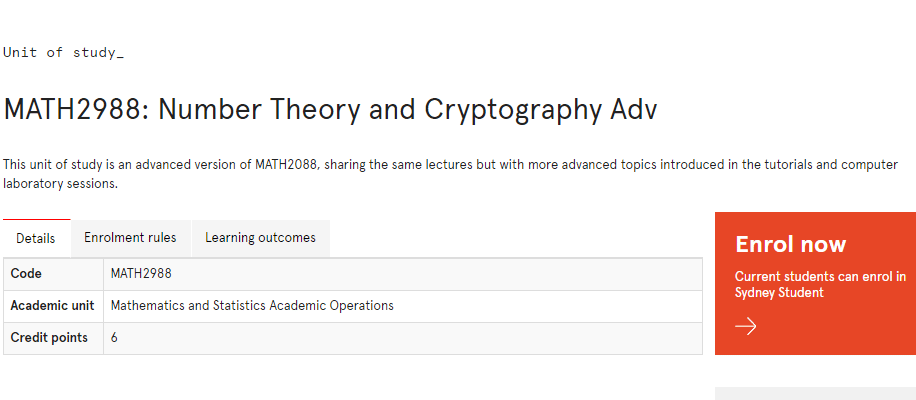
MATH2988简介
This unit of study is an advanced version of MATH2088, sharing the same lectures but with more advanced topics introduced in the tutorials and computer laboratory sessions.
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. understand and use the basic terminology of number theory and cryptography
- LO2. carry out simple number-theoretic computations either with a calculator or using MAGMA
- LO3. apply standard number-theoretic algorithms
- LO4. understand and use some classical and number-theoretic cryptosystems
- LO5. apply standard methods to attack some classical cryptosystems
- LO6. understand the theory underlying number-theoretic algorithms and cryptosystems, including the general properties of primes, prime factorisation, modular arithmetic, divisors and multiplicative functions, powers and discrete logarithms.
MATH2988 Number theory HELP(EXAM HELP, ONLINE TUTOR)
Show that if $e$ divides $a$ and $b$ then $e$ divides $a r+b s$ for any integers $r$ and $s$.
Solution:
Suppose $e$ divides $a$ and $b$. Then $a=k e$ and $b=j e$ for some integers $k$ and $j$. Thus:
$$
a r+b s=k e r+j e s=e(k r+j s)
$$
and therefore $e$ also divides $a r+b s$.
Use Euclid’s algorithm to find the following GCD’s:
(a) $(121,365)$,
(b) $(89,144)$,
(c) $(295,595)$,
(d) $(1001,1309)$.
Solution:
Use Euclid’s algorithm (ask me if you have doubts):
- $(121,365)=1$,
- $(89,144)=1$,
- $(295,595)=5$,
- $(1001,1309)=77$.
Find the GCD of 17017 and 18900 using Euclid’s algorithm.
Solution:
$(17017,18900)=7$, show your work!
Find $d$, the GCD of $a$ and $b$, i.e., $d=(a, b)$, and $r, s \in \mathbb{Z}$ such that $a r+b s=d$ :
(a) $a=267$ and $b=112$,
(b) $a=242$ and $b=1870$.
Solution:
Use Euclid’s and then backwards… show your work!
- $(267,112)=1$, and $r=-13$ and $s=31$, i.e. $267 \cdot(-13)+112 \cdot(31)=1$,
- $(242,1870)=22$ and $r=31$ and $s=-4$, i.e. $242 \cdot(31)+1870 \cdot(-4)=22$.

MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH2988 Number theory 数论的代写代考和辅导服务!