MY-ASSIGNMENTEXPERT™可以为您提供sydney DATA5711 Bayesian Analysis贝叶斯分析课程的代写代考和辅导服务!
这是悉尼大学贝叶斯分析课程的代写成功案例。
DATA5711课程简介
Increased computing power has meant that many Bayesian methods can now be easily implemented and provide solutions to problems that have previously been intractable. Bayesian methods allow researchers to incorporate prior knowledge into their statistical models. This unit is made up of three distinct modules, each focusing on a different niche in the application of Bayesian statistical methods to complex data in, for example, geophysics, ecology and hydrology. These include (but are not restricted to) Bayesian methods and models; statistical inversion; approximate Bayesian inference for semiparametric regression. Across all modules you will develop expertise in Bayesian computational statistics. On completion of this unit you will be able to apply appropriate Bayesian methods to a variety of applications in science, and other data-heavy disciplines to develop a better understanding of the information inherent in complex datasets.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. Demonstrate a coherent and advanced understanding of key concepts in computational statistics.
- LO2. Apply fundamental principles and results in statistics to solve given problems.
- LO3. Distinguish and compare the properties of different types of statistical models and statistical methods applicable to them.
- LO4. Identify assumptions required for various statistical methods to be valid and devise methods for testing these assumptions.
- LO5. Devise statistical solutions to complex problems.
- LO6. Adapt various computational techniques to build software for solving particular statistical problems.
- LO7. Communicate coherent statistical arguments appropriately to student and expert audiences, both orally and through written work.
DATA5711 Bayesian Analysis HELP(EXAM HELP, ONLINE TUTOR)
Suppose $\theta$ has the standard exponential distribution, and the conditional distribution of $y$ given $\theta$ is exponential with mean $1 / \theta$. Find the posterior density of $\theta$ given $y$.
The Bayesian model here is:
$$
\begin{aligned}
& f(y \mid \theta)=\theta e^{-\theta y}, y>0 \
& f(\theta)=e^{-\theta}, \theta>0
\end{aligned}
$$
So $f(\theta \mid y) \propto f(\theta) f(y \mid \theta) \propto e^{-\theta} \times \theta e^{-\theta y}=\theta^{2-1} e^{-\theta(y+1)}, y>0$.
This is the kernel of a gamma distribution with parameters 2 and $y+1$, as per the definitions in Appendix B.2. Thus we may write
$$
(\theta \mid y) \sim \operatorname{Gamma}(2, y+1),
$$
from which it follows that the posterior density of $\theta$ is
$$
f(\theta \mid y)=\frac{(y+1)^2 \theta^{2-1} e^{-\theta(y+1)}}{\Gamma(2)}, \theta>0 .
$$
Consider the Bayesian model given by:
$$
\begin{aligned}
& (y \mid \theta) \sim U(0, \theta) \
& \theta \sim U(0,1) .
\end{aligned}
$$
Find the posterior density of $\theta$ given $y$.
Noting that $0<y<\theta<1$, we see that the posterior density is
$$
\begin{aligned}
f(\theta \mid y)=\frac{f(\theta) f(y \mid \theta)}{f(y)} & =\frac{1 \times(1 / \theta)}{\int_y^1 1 \times(1 / \theta) d \theta} \
& =\frac{1 / \theta}{\log 1-\log y}=\frac{-1}{\theta \log y}, y<\theta<1 .
\end{aligned}
$$
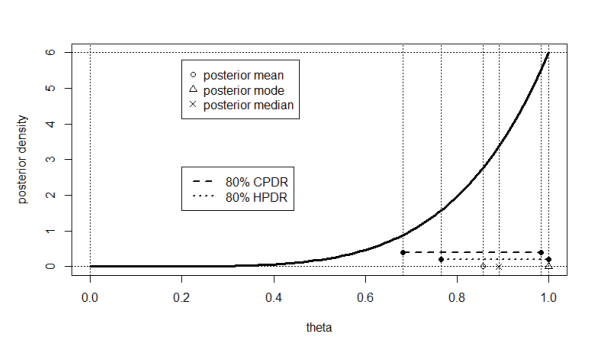
We have a bent coin, for which $\theta$, the probability of heads coming up, is unknown. Our prior beliefs regarding $\theta$ may be described by a standard uniform distribution. Thus no value of $\theta$ is deemed more or less likely than any other.
We toss the coin $n=5$ times (independently), and heads come up every time.
Find the posterior mean, mode and median of $\theta$. Also find the $80 \%$ HPDR and CPDR for $\theta$.
Recall the binomial-beta model:
$$
\begin{aligned}
& (y \mid \theta) \sim \operatorname{Binomial}(n, \theta) \
& \theta \sim \operatorname{Beta}(\alpha, \beta),
\end{aligned}
$$
for which $(\theta \mid y) \sim \operatorname{Beta}(\alpha+y, \beta+n-y)$.
We now apply this result with $n=y=5$ and $\alpha=\beta=1$ (corresponding to $\theta \sim U(0,1)$ ), and find that:
$$
\begin{aligned}
& (\theta \mid y) \sim \operatorname{Beta}(1+5,5-5+1)=\operatorname{Beta}(6,1) \
& f(\theta \mid y)=\frac{\theta^{6-1}(1-\theta)^{1-1}}{B(6,1)}=6 \theta^5, \quad 0<\theta<1 \
& F(\theta \mid y)=\int_0^\theta 6 t^5 d t=\theta^6, \quad 0<\theta<1 .
\end{aligned}
$$
$\begin{aligned} & \text { Therefore: } \begin{aligned} E(\theta \mid y) & =\frac{6}{6+1}=\frac{6}{7}=0.8571 \ \operatorname{Mode}(\theta \mid y) & =\frac{6-1}{(6-1)+(1-1)}=1 \ \operatorname{Median}(\theta \mid y) & =\text { solution in } \theta \text { of } F(\theta \mid y)=1 / 2, \text { i.e. } \theta^6=0.5 \ & =(0.5)^{1 / 6}=0.8909 .\end{aligned}\end{aligned}$

MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY DATA5711 BAYESIAN ANALYSIS贝叶斯分析课程的代写代考和辅导服务!