MY-ASSIGNMENTEXPERT™可以为您提供brandeis.edu Math56a Stochastic Porcesses随机过程课程的代写代考和辅导服务!
这是布兰戴斯大学 随机过程课程的代写成功案例。
Math56a 课程简介
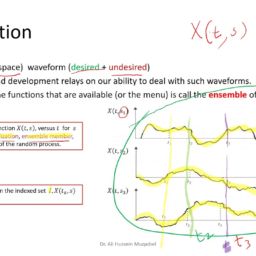
A stochastic process is a random process which evolves with time. The basic model is the Markov chain. This is a set of “states” together with transition probabilities from one state to another. For example, in simple epidemic models there are only two states: $S=$ “susceptible” and $I=$ “infected.” The probability of going from $S$ to $I$ increases with the size of $I$. In the simplest model The $S \rightarrow I$ probability is proportional to $I$, the $I \rightarrow S$ probability is constant and time is discrete (for example, events happen only once per day). In the corresponding deterministic model we would have a “difference equation.”
Prerequisites
In a continuous time Markov chain, transition events can occur at any time with a certain probability density. The corresponding deterministic model is a first order differential equation. This includes the “general stochastic epidemic.”
The number of states in a Markov chain is either finite or countably infinite. When the collection of states becomes a continuum, e.g., the price of a stock option, we no longer have a “Markov chain.” We have a more general stochastic process. Under very general conditions we obtain a Wiener process, also known as Brownian motion. The mathematics of hedging implies that stock options should be priced as if they are exactly given by this process. Ito’s formula explains how to calculate (or try to calculate) stochastic integrals which give the long term expected values for a Wiener process.
Math56a Stochastic Porcesses HELP(EXAM HELP, ONLINE TUTOR)
Let $Z \sim \mathcal{N}(0,1)$. We define $X_t$ for all $t \geq 0$ by $X_t=\sqrt{t} \cdot Z$. Then the stochastic process $X=$ $\left{X_t: t \geq 0\right}$ has continuous path and for all $t \geq 0$ we have $X_i \sim \mathcal{N}(0, t)$. Is $X_t$ a Brownian motion? (Check if all the conditions (a)-(c) on slide 9 from File $\mathrm{F}$ hold for $X_t$. In particular, the variance of the increments.)
Let $B(t)$ be the one-dimensional Brownian motion. Show that $\operatorname{Cov}(B(t), B(s))=\min {s, t}$.
Let $B(t)$ be the one-dimensional Brownian motion. Fix an arbitrary positive number $s$. Show that the process $B(t+s)-B(s)$ is also Brownian motion.
Let $B(t)$ be the one-dimensional Brownian motion. Consider the following stochastic process: $V(0):=$ and $V(t)=t B(1 / t)$. Prove that $V(t)$ is also a Brownian motion.
Let $B(t)$ be the one-dimensional Brownian motion. Consider the following stochastic process: $V(0):=$ and $V(t)=t B(1 / t)$. Prove that $V(t)$ is also a Brownian motion.
(1) Let $\left(N_t\right){t \geq 0}$ be a Poisson process with intensity $\lambda>0$ and let $\left(X_i\right){i \geq 0}$ be a sequence of i.i.d. random variables, independent of $N$. Show that if $g(s, x)$ is a function and $T_j$ are jump times of $N$ then
$$
\mathbb{E}\left[\exp \left(\theta \sum_1^{N_t} g\left(T_j, X_j\right)\right)\right]=\exp \left(\lambda \int_0^t d s \mathbb{E}\left[e^{\theta g(s, X)}-1\right]\right) .
$$
This is called Campbell’s Theorem.
(2) Cars arrive at the beginning of a long road in a Poisson stream of intensity $\lambda$ from time $t=0$ onwards. A car has a fixed velocity $V$ miles per hour, where $V>0$ is a random variable. The velocities of cars are i.i.d. and are independent of the arrival process. Cars can overtake each other freely. Show that the number of cars on the first $x$ miles of the road at time $t$ has a Poisson distribution with mean $\lambda \mathbb{E}[\min {t, x / V}]$.
(Optional, 3 bonus points) Customers enter a supermarket as a Poisson process with intensity 2. There are two salesmen near the door who offer passing customers samples of a new product. Each customer takes an exponential time of parameter 1 to think about the new product, and during this time occupies the full attention of one salesman. Having tried the product, customers proceed into the store and leave by another door. When both salesmen are occupied, customers walk straight in. Assuming that both salesmen are free at time 0 , find the probability that both are busy at a later time $t$.

MY-ASSIGNMENTEXPERT™可以为您提供BRANDEIS.EDU MATH56A STOCHASTIC PORCESSES随机过程课程的代写代考和辅导服务!