MY-ASSIGNMENTEXPERT™可以为您提供 suny MATH3020 Graph Theory图论的代写代考和辅导服务!
这是帝国州大学 图论课程的代写成功案例。
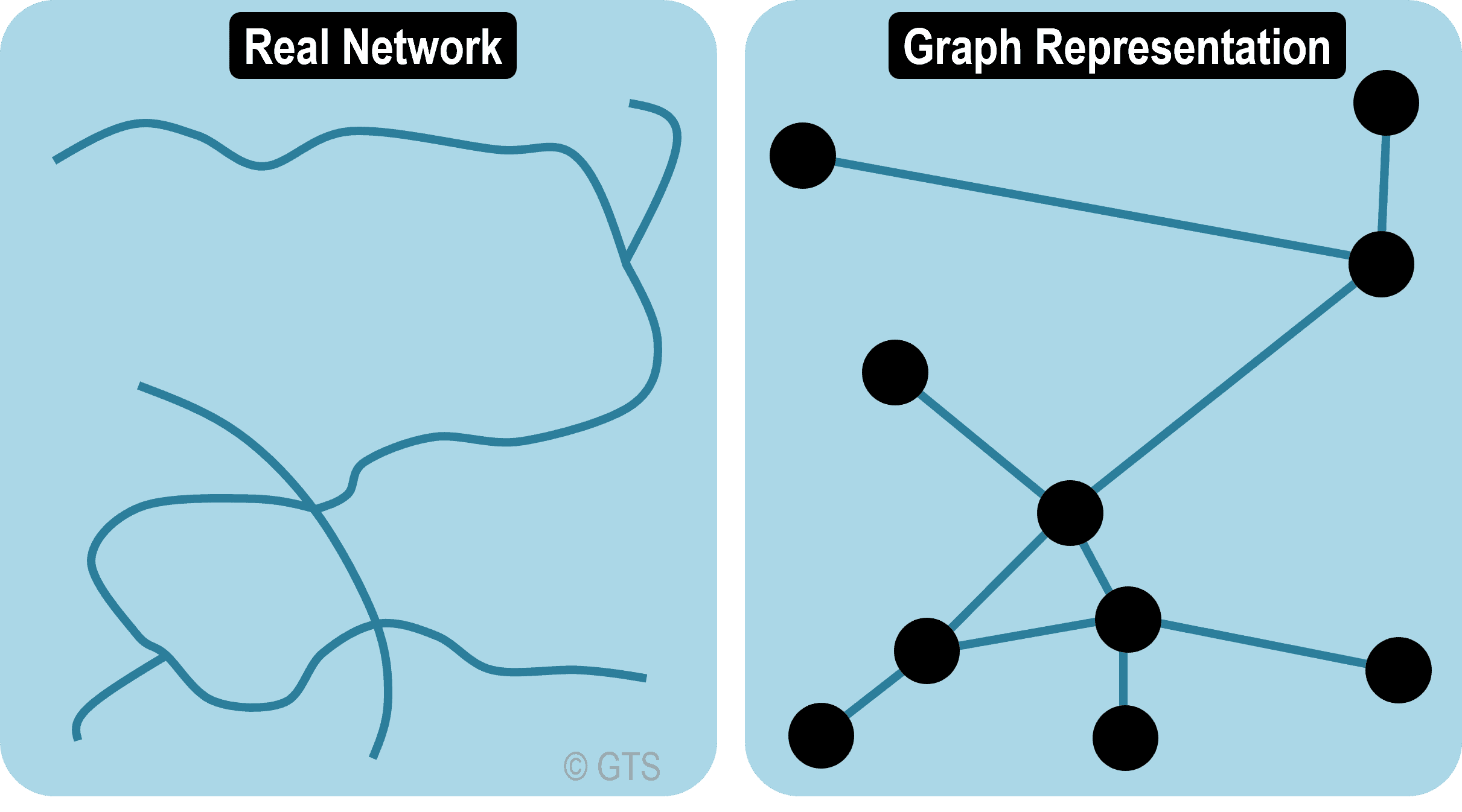
MATH3020课程简介
You will learn the same curriculum as our on-campus students
Topics covered in this course include: graphs as models, paths, cycles, directed graphs, trees, spanning trees, matchings (including stable matchings, the stable marriage problem and the medical school residency matching program), network flows, and graph coloring (including scheduling applications). Students will explore theoretical network models, such as random graphs, small world models and scale-free networks, as well as networked datasets from social, infrastructure and information networks, the role of strong and weak ties, triadic closure, and centrality measures, as well as the fragility of networked systems and contagious process on networks of various topologies. Prerequisites: Discrete Math Foundations of mathematics and mathematical proof: logic, methods of proof (both inductive and deductive), sets, relations and functions. This knowledge may be obtained from a course such as Discrete Mathematics, for example. This course was previously SMT-273244.
Prerequisites
About our University College
Our university college is a leader in undergraduate instruction. We provide bachelor’s and master’s degrees in liberal arts and sciences and professional disciplines. Student success is our primary focus as evidenced by faculty and staff interactions through honors programs, independent study opportunities, research and study abroad.
MATH3020 Graph Theory HELP(EXAM HELP, ONLINE TUTOR)
(i) Let $S$ be a finite family of closed axis-parallel squares of side length 1 in the plane. Assume also that any point in the plane belongs to at most 2 squares of $S$. Prove that the family $S$ can be partitioned into four sub-families such that each sub-family consists of pairwise disjoint squares.
(ii) Let $S$ be as above without the restriction on the side length. Thats is, $S$ is a finite family of closed axis-parallel squares. Assume also that any point in the plane belongs to at most 2 squares of $S$. Prove that the family $S$ can be partitioned into five sub-families such that each sub-family consists of pairwise disjoint squares.
Let $G$ be a $d$-degenerate graph and let $G^{\prime}$ be the graph obtained from $G$ by Mycielski’s construction. Is it true that $G^{\prime}$ is $d+1$ degenerate?
Find the formula for $\tau\left(K_{n, n}\right)$. That is, the number of spanning trees of the complete bipartite graph $K_{n, n}$.
For $n \geq 4$ let $G$ be a simple $n$-vertex graph with $e(G) \geq 2 n-3$. Prove that $G$ has two cycles of equal length.
Show that the $n$-CUBE $Q_n$ and the Boolean lattice $B L_n$ (see HW 1 , Problems 4 and 5 for the definitions of these graphs) are connected for every natural number $n$.
Let $W$ be a walk of length at least 1 whose first and last endpoints are the same. Moreover, suppose $W$ does not contain a cycle. Show that some edge of $W$ repeats immediately (once in each direction).
Let $G$ be a simple graph with $n$ vertices and $m$ edges. Show that if $m>\left(\begin{array}{c}n-1 \ 2\end{array}\right)$, then $G$ is connected. For every $n>1$, find a disconnected simple graph $G$ with $m=\left(\begin{array}{c}n-1 \ 2\end{array}\right)$.
MY-ASSIGNMENTEXPERT™可以为您提供 suny MATH3020 Graph Theory图论的代写代考和辅导服务!