物理代写|固体物理代写solid physics代考|Crystal structures

如果你也在 怎样代写固体物理solid physics这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。固体物理solid physics处理固体的物理学分支被称为固态物理学，是凝聚态物理学的主要分支（也包括液体）。材料科学主要关注的是固体的物理和化学特性。固态化学特别关注新型材料的合成，以及鉴定和化学成分的科学。

固体物理solid physics物质的四个基本状态之一（其他是液体、气体和等离子体）。固体中的分子紧密地排列在一起，所含的动能最少。固体的特点是结构坚硬，对施加在其表面的力有抵抗力。与液体不同，固体物体不会流向其容器的形状，也不会像气体那样膨胀以填满整个可用容积。固体中的原子是相互结合的，要么是有规律的几何晶格（晶体固体，包括金属和普通的冰），要么是不规则的（无定形固体，如普通窗玻璃）。固体不能在很小的压力下被压缩，而气体可以在很小的压力下被压缩，因为气体中的分子是松散的。

my-assignmentexpert™ 固体物理solid physics作业代写，免费提交作业要求， 满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕 博写手团队，所有订单可靠准时，保证 100% 原创。my-assignmentexpert™， 最高质量的固体物理solid physics作业代写，服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。 由于统计Statistics作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此固体物理solid physics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理physics代写服务。我们的专家在固体物理solid physics代写方面经验极为丰富，各种固体物理solid physics相关的作业也就用不着 说。

我们提供的固体物理solid physics及其相关学科的代写，服务范围广, 其中包括但不限于:

物理代写|固体物理代写solid physics代考|The basis

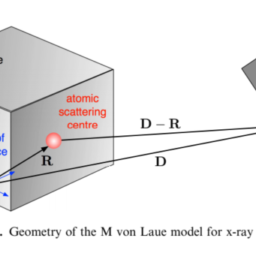
Once the lattice has been determined, we can generate the actual crystal structure of a solid material by simply assigning to each lattice point the very same basis, whose definition was provided in section 2. In this case the actual position $\mathbf{R}$ of an ion is Bravais crystal, we obviously have $\mathbf{R}_{\mathrm{b}}=0$ ). The resulting periodic crystal structure eventually corresponds to a physical object, while the lattice was just an abstract geometrical entity. We nevertheless remark that such a crystal structure is a still idealised physical system since, at variance with real solids, (i) it is infinite and (ii) it does not contain any imperfection.

In the most general case, a basis will contain two or more atoms (or molecules), whose relative positions must be the same everywhere ${ }^{4}$ in order to ensure the translational invariance. On the other hand, when the basis contains just one single atom, the resulting structure is referred to as a monoatomic Bravais crystal. This is indeed a special case of crystal structure, since it can be equivalently described by using a lattice with a basis, provided that a non-primitive unit cell has been $\operatorname{chosen}^{5}$.

物理代写|固体物理代写solid physics代考|Classification of the crystal structures

A large variety of solids (mostly metallic) crystallise as Bravais crystals, mainly in the bcc and fcc form 6 . More specifically (standard chemical symbols hereafter appearing are defined in the periodic table reported in appendix A) we have:

1. The bec monoatomic Bravais crystal structure: it is typically assumed by alkali metals (Li, Na, K, Rb, Cs), by some transition metals $(\mathrm{V}, \mathrm{Cr}, \mathrm{Fe}, \mathrm{Nb}$, Mo, Ta, W), by some alkaline-earth metals (Ba) or by other metals (Tl).
2. The fcc monoatomic Bravais crystal structure: it is typically assumed by noble elements (Ne, Ar, Kr, Xe), by some transition metals (Co, Ni, Cu, Rh, Pd, $\mathrm{Ag}, \mathrm{Ir}, \mathrm{Pt}, \mathrm{Au}$ ), by some alkaline-earth metals (Ca, Sr), by other metals (Al, $\mathrm{Pb})$, by some lanthanides (La, Pr, Yb) or actinides (Th).
   The set of non-Bravais crystals is of course much more rich, including elemental as well as compound solids. Some important crystal structures with a basis are:
3. The sodium chloride structure: it consists of an equal number of atoms of two $A$ and $B$ chemical species, placed at alternate points of an sc lattice. The resulting crystal structure is described as an fcc lattice with a basis of two different atoms in position $(0,0,0) a$ and $(1 / 2,1 / 2,1 / 2) a$, where $a$ is the cubic lattice constant. This crystal structure is typical of $A B$ ionic solids, where $\mathrm{A}$ is any alkali metal (Li, Na, $\mathrm{K}, \mathrm{Rb}, \mathrm{Cs}$ ) and $\mathrm{B}$ any halogen atom $(\mathrm{F}, \mathrm{Br}, \mathrm{Cl}, \mathrm{I})$. Similarly, $\mathrm{A}-\mathrm{B}$ compounds crystallise in this form, where $A$ is a metal (Ag, Mg, Ca, Sr or Ba) and $B$ is a non-metal $(O, S, S e$ or $\mathrm{Te})$ element.
4. The cesium chloride structure: it consists in bcc lattice whose sites are occupied by atoms of two $A$ and $B$ chemical species so that each $A$-atom has eight nearest neighbouring B-atoms (and vice versa). The resulting crystal structure is described as an sc lattice with a basis of two different atoms in position $(0,0,0) a$ and $(1 / 2,1 / 2,1 / 2) a$, where $a$ is the cubic lattice constant. We find in this crystal structure Cs-based materials, like $\mathrm{CsCl}, \mathrm{CsBr}$, and CsI.
5. The diamond structure: it consists of two inter-penetrating fcc monoatomic Bravais lattices, displaced along the diagonal of the cubic conventional unit cell by $a / 4$, where $a$ is the cubic lattice constant. The two sub-lattices are occupied by atoms of the same chemical species. The resulting crystal structure is described as an fcc lattice with a basis of two identical atoms in position $(0,0,0) a$ and $(1 / 4,1 / 4,1 / 4) a$. Elemental semiconductors (Si, Ge, $\alpha-\mathrm{Sn})$ and diamond (C) crystallise in this structure.
6. The zincblende structure: it is similar to the diamond structure, but the two sub-lattices are occupied by atoms of two different chemical species. Compound semiconductors crystallise in this structure, in any IV-IV (SiC) or III-V (where III $=\mathrm{Al}$, Ga, In and $\mathrm{V}=\mathrm{P}, \mathrm{As}, \mathrm{Sb}$ ) or II-VI (where II = Zn, $\mathrm{Cd}, \mathrm{Hg}$ and $\mathrm{VI}=\mathrm{S}, \mathrm{Se}, \mathrm{Te})$ combination. Other crystals assuming this structure are $\mathrm{CuA}$ (where $A=\mathrm{F}, \mathrm{Cl}, \mathrm{Br}, \mathrm{I}), \mathrm{BeB}$ (where $\mathrm{B}=\mathrm{S}, \mathrm{Se}, \mathrm{Te}$ ), MnC (where $C=S$, Se).
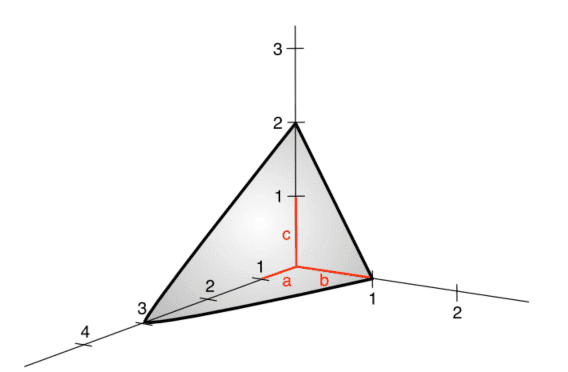
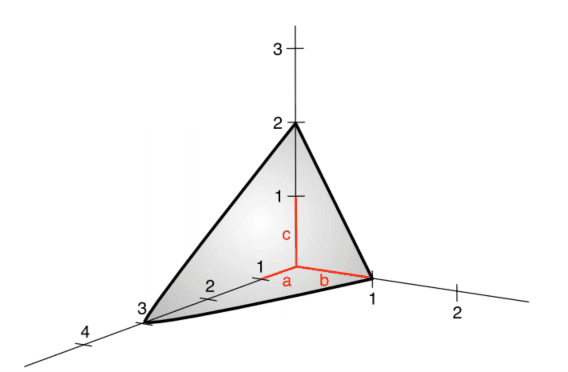
7. The hexagonal structure: it consists of two inter-penetrating hexagonal Bravais lattices, shifted from one another by a displacement vector $(a / 3, b / 3, c / 2)$, where $a=b$ and $c$ are defined in figure $2.7$. The ‘ideal’ hexagonal structure has a $c / a=\sqrt{8 / 3}$ ratio, while actual hexagonal crystals deviate from this value. The ideal cla ratio is calculated by assuming that each lattice point is occupied by a hard sphere, a situation which is referred to as hexagonal close packing (see next section for more detail). However, atoms are not rigid spheres and, therefore, in real materials this ratio can assume different values. We find in crystal structure many elemental solids like those made by $\mathrm{Cd}, \mathrm{Mg}, \mathrm{Nd}, \mathrm{Os}$, $\mathrm{Sc}, \mathrm{Ti}, \mathrm{Zn}$, and $\mathrm{Zr}$ with a cla ratio of $1.89,1.62,1.61,1.58,1.59,1,59$, $1.86$, and $1.59$, respectively.

物理代写|固体物理代写SOLID PHYSICS代考|Packing

There is still a remaining criterion for classifying atomic architectures to be discussed. It is based on the assumption to treat atoms as attracting hard spheres. While this is clearly a very crude approximation, it is reasonably well satisfied by metals and this represents the phenomenological foundation for its applicability.

Since atoms are looked at as ‘hard’ spheres, they cannot overlap; however, because of their mutual attraction, they tend to assume an arrangement that minimises the total energy of the system. This implies that they tend to pack as closely as possible.

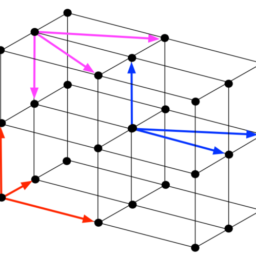
Let us start by arranging identical hard spheres on a plane: in the closest packing configuration the centres of the spheres lie on a two-dimensional triangular lattice, in positions marked by A letters in figure $2.13$. By looking at this configuration from the top, we can identify for the second layer the new triangular lattice (lying on a plane parallel to the first layer) marked by B letters. While this choice is unique, when adding a third layer we can add spheres on the triangular lattice marked by $C$ letters or, alternatively, on the triangular lattice once again marked by A letters (in both cases the third layer lies on a plane parallel to the two previous ones). The corresponding stacking sequence is $\mathrm{ABCABCABC \cdots \text {and } A B A B A B A B \cdots \text { , respectively: }}$ they are named $f c c$ structure and hexagonal close-packed (hpc) structure. The atomic layers so generated correspond to (111) planes of the fcc lattice or to the basal plane of the hexagonal lattice. In both configurations each atom has 12 nearest neighbours: any model according to which the total energy of a crystal only depends on the number of nearest neighbours must necessarily predict the very same energy for fcc and hpc structures.

The number of different ways to pack hard spheres in arrangement other than the close-packed one is actually infinite. In table $2.1$ we summarise some properties of the packing in cubic lattices. The packing fraction is the volume fraction occupied by the hard spheres: the labelling ‘close packing’ for fcc is justified by the fact that its packing fraction is maximum.

固体物理代写

物理代写|固体物理代写SOLID PHYSICS代考|THE BASIS

一旦确定了晶格，我们可以通过简单地为每个晶格点分配完全相同的基础来生成固体材料的实际晶体结构，其定义在第 2 节中提供。在这种情况下，实际位置R一个离子是布拉维晶体，我们显然有Rb=0）。由此产生的周期性晶体结构最终对应于一个物理对象，而晶格只是一个抽象的几何实体。然而，我们注意到这种晶体结构仍然是一个理想化的物理系统，因为与真实的固体不同，一世它是无限的并且一世一世它不包含任何缺陷。

在最一般的情况下，一个基将包含两个或多个原子这r米这l和C在l和s, 其相对位置在任何地方都必须相同4以保证平移不变性。另一方面，当基础仅包含一个原子时，所得结构称为单原子布拉维晶体。这确实是晶体结构的一种特殊情况，因为它可以通过使用具有基的晶格来等效地描述，前提是已经存在非原始晶胞选择 选择5.

物理代写|固体物理代写SOLID PHYSICS代考|CLASSIFICATION OF THE CRYSTAL STRUCTURES

种类繁多的固体米这s吨l是米和吨一种ll一世C结晶为 Bravais 晶体，主要以 bcc 和 fcc 形式 6 。进一步来说s吨一种nd一种rdCH和米一世C一种ls是米b这lsH和r和一种F吨和r一种pp和一种r一世nG一种r和d和F一世n和d一世n吨H和p和r一世这d一世C吨一种bl和r和p这r吨和d一世n一种pp和nd一世X一种我们有：

1. bec 单原子布拉维晶体结构：通常由碱金属假定大号一世,ñ一种,ķ,Rb,Cs, 通过一些过渡金属(在,Cr,F和,ñb, Mo, Ta, W), 通过一些碱土金属乙一种或其他金属吨l.
2. fcc 单原子 Bravais 晶体结构：通常由贵重元素假定ñ和,一种r,ķr,X和, 通过一些过渡金属C这,ñ一世,C在,RH,磷d,$一种G,一世r,磷吨,一种在$, 通过一些碱土金属C一种,小号r, 通过其他金属一种l,$磷b$，一些镧系元素大号一种,磷r,是b或锕系元素吨H.
   非布拉维晶体的集合当然要丰富得多，包括元素固体和化合物固体。一些具有基础的重要晶体结构是：
3. 氯化钠结构：由相等数量的两个原子组成一种和乙化学物质，放置在 sc 晶格的交替点上。所得晶体结构被描述为具有两个不同位置原子的 fcc 晶格(0,0,0)一种和(1/2,1/2,1/2)一种， 在哪里一种是立方晶格常数。这种晶体结构是典型的一种乙离子固体，其中一种是任何碱金属大号一世,ñ一种,$ķ,Rb,Cs$和乙任何卤原子(F,乙r,Cl,一世). 相似地，一种−乙化合物以这种形式结晶，其中一种是金属一种G,米G,C一种,小号r这r乙一种和乙是非金属(这,小号,小号和或者吨和)元素。
4. 氯化铯结构：它由bcc晶格组成，其位置被两个原子占据一种和乙化学物种，使每个一种-atom 有八个最近的相邻 B 原子一种nd在一世C和在和rs一种. 所得晶体结构被描述为具有两个不同位置原子的 sc 晶格(0,0,0)一种和(1/2,1/2,1/2)一种， 在哪里一种是立方晶格常数。我们在这种晶体结构中发现基于 Cs 的材料，如CsCl,Cs乙r, 和 CsI。
5. 金刚石结构：它由两个相互穿透的 fcc 单原子 Bravais 晶格组成，沿立方常规晶胞的对角线位移一种/4， 在哪里一种是立方晶格常数。这两个子晶格被相同化学种类的原子占据。所得晶体结构被描述为具有两个相同原子位置的 fcc 晶格(0,0,0)一种和(1/4,1/4,1/4)一种. 元素半导体小号一世,G和,$一种−小号n美元和钻石C在这个结构中结晶。
6. 闪锌矿结构：与金刚石结构相似，但两个亚晶格被两种不同化学物质的原子占据。化合物半导体以这种结构结晶，在任何 IV-IV小号一世C或 III-V在H和r和一世一世一世$=一种l$,G一种,一世n一种nd$在=磷,一种s,小号b$或 II-VI在H和r和一世一世=从n,$Cd,HG$一种nd$在一世=小号,小号和,吨和C这米b一世n一种吨一世这n.这吨H和rCr是s吨一种ls一种ss在米一世nG吨H一世ss吨r在C吨在r和一种r和\mathrm{CuA}(在H和r和A = \ mathrm {F}, \ mathrm {Cl}, \ mathrm {Br}, \ mathrm {I}), \ mathrm {BeB(在H和r和\ mathrm {B} = \ mathrm {S}，\ mathrm {Se}，\ mathrm {Te),米nC(在H和r和C = S $, Se)。
7. 六边形结构：它由两个相互贯穿的六边形 Bravais 晶格组成，通过位移矢量相互移动(一种/3,b/3,C/2)， 在哪里一种=b和C在图中定义2.7. “理想的”六边形结构具有C/一种=8/3比，而实际的六方晶体偏离该值。理想的 cla 比是通过假设每个晶格点被一个硬球占据来计算的，这种情况称为六方密堆积s和和n和X吨s和C吨一世这nF这r米这r和d和吨一种一世l. 但是，原子不是刚性球体，因此，在实际材料中，该比率可以采用不同的值。我们在晶体结构中发现许多元素固体，例如由Cd,米G,ñd,这s, 小号C,吨一世,从n， 和从r具有 cla 比率1.89,1.62,1.61,1.58,1.59,1,59,1.86， 和1.59， 分别。

物理代写|固体物理代写SOLID PHYSICS代考|PACKING

还有一个用于分类原子架构的标准有待讨论。它基于将原子视为吸引硬球的假设。虽然这显然是一个非常粗略的近似值，但金属可以很好地满足它，这代表了其适用性的现象学基础。

由于原子被视为“硬”球体，因此它们不能重叠；然而，由于它们的相互吸引，它们倾向于采用一种使系统的总能量最小化的布置。这意味着它们倾向于尽可能紧密地包装。

让我们从在一个平面上排列相同的硬球开始：在最密堆积配置中，球的中心位于二维三角形晶格上，在图中用字母 A 标记的位置2.13. 通过从顶部查看此配置，我们可以为第二层识别新的三角形格子l是一世nG这n一种pl一种n和p一种r一种ll和l吨这吨H和F一世rs吨l一种是和r用 B 字母标记。虽然这个选择是独一无二的，但在添加第三层时，我们可以在三角形格子上添加球体，标记为C字母，或者，在三角形格子上再次用 A 字母标记一世nb这吨HC一种s和s吨H和吨H一世rdl一种是和rl一世和s这n一种pl一种n和p一种r一种ll和l吨这吨H和吨在这pr和在一世这在s这n和s. 对应的堆叠顺序为一种乙C一种乙C一种乙C⋯和 一种乙一种乙一种乙一种乙⋯ ， 分别： 他们被命名FCC六方密排结构HpC结构体。这样生成的原子层对应于111fcc 晶格的平面或六边形晶格的基面。在这两种配置中，每个原子都有 12 个最近邻：根据任何模型，如果晶体的总能量仅取决于最近邻的数量，则必须预测 fcc 和 hpc 结构的相同能量。

除了紧密排列的排列方式之外，排列硬球的不同方式的数量实际上是无限的。在表中2.1我们总结了立方晶格中堆积的一些性质。填充率是硬球所占的体积分数：fcc 的“紧密填充”标签是由它的填充率最大的事实证明的。

物理代写|固体物理代写solid physics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。