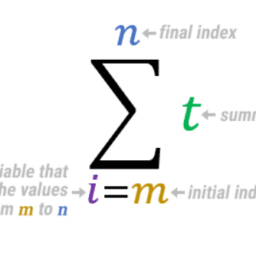Problem 1. According to Anna, the number 2021 is fantabulous. She states that if any element of the set ${m, 2 m+1,3 m}$ is fantabulous for a positive integer $m$, then they are all fantabulous. Is the number $2021^{2021}$ fantabulous?
(Australia, Angelo Di Pasquale)
Answer: Yes
Solution $1 .$
Consider the sequence of positive integers $m, 3 m, 6 m+1,12 m+3,4 m+1,2 m$. Since each number in the sequence is fantabulous if and only if the next one is, we deduce that $m$ is fantabulous if and only if $2 m$ is fantabulous.
Combined with the fact that $m$ is fantabulous if and only if $2 m+1$ is fantabulous, this implies that $m>1$ is fantabulous if and only if $f(m)=\left[\frac{m}{2}\right]$ is fantabulous. We can apply $f$ sufficiently many times to any positive integer $n$ to conclude that $n$ is fantabulous if and only if 1 is fantabulous. Therefore, the fact that 2021 is fantabulous implies that 1 is fantabulous, which in turn implies that $2021^{2021}$ is fantabulous.
Problem 2. Find all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ such that the equation
$f(x f(x)+y)=f(y)+x^{2}$
holds for all rational numbers $x$ and $y$.
Here, $\mathbb{Q}$ denotes the set of rational numbers.
(Slovakia, Patrik Bak)
Answer: $f(x)=x$ and $f(x)=-x$.
Solution. Denote the equation from the statement by (1). Let $x f(x)=A$ and $x^{2}=B$. The equation Solution. Denote the equation from (1) is of the form
Also, if we put $y \rightarrow-A+y$, we have $f(A-A+y)=f(-A+y)+B$. Therefore
$$
f(-A+y)=f(y)-B
$$
We can easily show that for any integer $n$ we even have
$$
f(n A+y)=f(y)+n B
$$
Indeed, it’s trivially true for $n=0$ and if this holds true for some integer $n$, then
$$
f((n+1) A+y)=f(A+y+n A)=f(n y+A)+B=f(y)+n B+B=f(y)+(n+1) B
$$
and
$$
f((n-1) A+y)=f(-A+n A+y)=f(n A+y)-B=f(y)+n B-B=f(y)+(n-1) B .
$$
So, equation (2) follows from the induction on $n$.
Now we can say that for any integer $k$ it holds
$$
f(n x f(x)+y)=f(y)+n x^{2}
$$
If $y$ is given, then $f(y)+n x^{2}$ can be any rational number, since $n x^{2}$ can be any rational number. If it is supposed to be $\frac{p}{q}$, where $q \neq 0$, then we may take $n=p q$, and $x=\frac{1}{q}$. Therefore $f$ is surjective on $Q$. So there’s a rational number $c$ such that $f(c)=0$. Be putting $x=c$ into (1) we immediately get $c=0$, i.e. $f(0)=0$. Therefore, $f(x)=0$ if and only if $x=0$.
For any integer $n$ and for any rational $x, y$ it holds
$$
f\left(n^{2} x f(x)+y\right)=f(y)+n^{2} x^{2}=f(y)+(n x)^{2}=f(n x f(n x)+y)
$$
After taking $y=-n x f(n x)$ in (4), the right-hand side becomes 0 , therefore
$$
n^{2} x f(x)-n x f(n x)=0
$$
This simplifies into $n f(x)=f(n x)$ for $x \neq 0$, but it also holds for $x=0$. Therefore, for any rational number $x=\frac{p}{q}$ we have,
$$
f(x)=f\left(\frac{p}{q}\right)=f\left(p \cdot \frac{1}{q}\right)=p \cdot f\left(\frac{1}{p}\right)=p \cdot \frac{f\left(q \cdot \frac{1}{q}\right)}{q}=\frac{p}{q} \cdot f(1)=x f(1)
$$
So, we have $f(x)=k x$, for some rational number $k$. Let’s put this answer in (1) and we get $k(x k x+y)=k y+x^{2}$, thus $k^{2}=1$. Therefore $f(x)=x$ and $f(x)=-x$ are solutions.
Problems 5. A plane has a special point $O$ called the origin. Let $P$ be a set of 2021 points in the plane, such that
(i) no three points in $P$ lie on a line and
(ii) no two points in $P$ lie on a line through the origin.
A triangle with vertices in $P$ is fat, if $O$ is strictly inside the triangle. Find the maximum number of fat triangles.
(Austria, Veronika Schreitter)
Answer: $2021 \cdot 505 \cdot 337$
Solution
We will count minimal number of triangles that are not fat. Let $F$ set of fat triangles, and $\mathrm{S}$ set of triangles that are not fat. If triangle $X Y Z \in S$, we call $X$ and $Z$ good vertices if $O Y$ is located between $O X$ and $O Z$. For $A \in P$ let $S_{A} \subseteq S$ be set of triangles in $S$ for which $A$ is one of the good vertex.
It is easy to see that
$$
2|S|=\sum_{A \in P}\left|S_{A}\right|
$$
For $A \in P$, let $R_{A} \subset P$ and $L_{A} \subset P$ be parts of $P \backslash{A}$ divided by $A O$. Suppose for $A X Y \in S$ vertex $A$ is good, then clearly $X, Y \in R_{A}$ or $X, Y \in L_{A} .$ On the other hand, if $X, Y \in R_{A}$ or $X, Y \in L_{A}$ then clearly $A X Y \in S$ and $A$ is its good vertex. Therefore,
$$
\left|S_{A}\right|=\left(\begin{array}{c}
\left|R_{A}\right| \
2
\end{array}\right)+\left(\begin{array}{c}
\left|L_{A}\right| \
2
\end{array}\right)
$$
It is easy to show following identity:
$$
\frac{x(x-1)}{2}+\frac{y(y-1)}{2}-2 \cdot \frac{\frac{x+y}{2}\left(\frac{x+y}{2}-1\right)}{2}=\frac{(x-y)^{2}}{4}
$$
By using (2) and (3) we get
$$
\left|S_{A}\right| \geq 2 \cdot\left(\begin{array}{c}
\frac{\left|R_{A}\right|+\left|L_{A}\right|}{2} \
2
\end{array}\right)=2 \cdot\left(\begin{array}{c}
1010 \
2
\end{array}\right)=1010 \cdot 1009
$$
and the equality holds when $\left|R_{A}\right|=\left|L_{A}\right|=1010$. Hence
$$
|S|=\frac{\sum_{A \in P}\left|S_{A}\right|}{2} \geq \frac{2021 \cdot 1010 \cdot 1009}{2}=2021 \cdot 505 \cdot 1009
$$
Therefore,
$$
|F|=\left(\begin{array}{c}
2021 \
3
\end{array}\right)-|S| \leq 2021 \cdot 1010 \cdot 673-2021 \cdot 505 \cdot 1009=2021 \cdot 505 \cdot 337
$$
For configuration of points on regular 2021-gon which is centered at $O$, inequalities in $(4),(5),(6)$ become equalities. Hence $2021 \cdot 505 \cdot 337$ is indeed the answer.

real analysis代写analysis 2, analysis 3请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
组合数学代考
统计作业代写
European Girls’ Mathematical Olympiad
The European Girls’ Mathematical Olympiad is an international mathematics competition similar in style to the International Mathematical Olympiad, with two papers taken on consecutive days. Participating countries send teams consisting of four female mathematicians of school age. EGMO 2012 was held in Cambridge, United Kingdom in April 2012, EGMO 2013 was held in Luxembourg, EGMO 2014 was held in Turkey, EGMO 2015 was held in Belarus, EGMO 2016 was held in Romania, EGMO 2017 was held in Switzerland, EGMO 2018 was held in Italy, EGMO 2019 was held in Ukraine, EGMO 2020 was planned to be held in the Netherlands but took place as a purely virtual event because of the COVID-19 pandemic, EGMO 2021 was planned to be held in Georgia but also took place as a purely virtual event for the same reason and EGMO 2022 will be held in Hungary.
The EGMO Board consists of three members elected for three-year terms and three representatives of EGMO host countries. The current elected members are:
- Viviane Kehl (President) (Switzerland) (current term extended from 2021 to 2022, elections postponed to EGMO 2022)
- Slagjana Brsakoska (North Macedonia) (current term ends 2022)
- Elisa Lorenzo García (Spain) (current term extended from 2021 to 2022, elections postponed to EGMO 2022)
The host country representatives are:
- Ivane Gokadze (Georgia, EGMO 2021)
- Melinda Flóra Kiss (Hungary, EGMO 2022)
- EGMO 2023 host country to be announced
EGMO: EGMO 2022 in Hungary
| EGMO number | 11 |
|---|---|
| Year | 2022 (home page) |
| Country | Hungary |
| City | Eger (hybrid) |
| Start date | 2022-04-06 |
| End date | 2022-04-12 |
| Contact name | Ágnes Backhausz |
| Contact email | [email protected] |
Lists of currently registered countries and participants are available, as is the live scoreboard.
Extra information available: