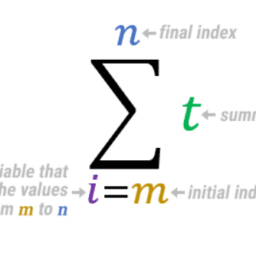0 0

By admin 数学代写 2022年2月22日

where, as indicated, $C=\sum_{k=0}^{n-1}\left(\begin{array}{c}n \ k\end{array}\right)|x|^{k}$. Let $\delta$ be small enough that the right side is less than $\left|x^{n}-a\right|$. For example, you could let $\delta=\min \left(\frac{\left|x^{n}-a\right|}{2 C}, 1\right)$. Then if $y \in(x-\delta, x+\delta)$
$$
\left|y^{n}-x^{n}\right| \leq C|x-y|<C \delta \leq\left|x^{n}-a\right|
$$
It follows that on the number line, $y^{n}$ must be between $a$ and $x^{n}$. Consequently, $y^{n}-a \neq 0$ and has the same sign as $x^{n}-a$. (Draw a picture.)
Theorem $2.11 .2$ Let $a>0$ and let $n>1$. Then there exists a unique $x>0$ such that $x^{n}=a$.
Proof: Let $S$ denote those numbers $y \geq 0$ such that $t^{n}-a<0$ for sll $t \in[0, y]$. One such number is 0 . If $a \geq 1$, then a short proof by induction shows $a^{n}>a$ and so, in this case, $S$ is bounded above by $a$. If $a<1$, then another short argument shows $(1 / a)^{n}>a$ and so $S$ is bounded above by $1 / a$. By completeness, there exists $x$, the least upper bound of $S$. Thus for all $y \leq x, y^{n}-a<0$ since if this is not so, then $x$ was not a least upper bound to $S$. If $x^{n}-a>0$, then by the lemma, $y^{n}-a>0$ on some interval $(x-\delta, x+\delta)$. Thus $x$ fails to be a the least upper bound because an upper bound is $x-\delta / 2$. If $x^{n}-a<0$, then by the lemma, $y^{n}-a<0$ on some interval $(x-\delta, x+\delta)$ and so $x$ is not even an upper bound because $S$ would then contain $[0, x+\delta)$. Hence the only other possibility is that $x^{n}-a=0$. That is, $x$ is an $n^{\text {th }}$ root of $a$.
This has shown that $a$ has a positive $n^{\text {th }}$ root. Could it have two? Suppose $x, z$ both work. If $z>x$, then by the binomial theorem,
$$
\begin{aligned}
z^{n} &=(x+z-x)^{n}=\sum_{k=0}^{n}\left(\begin{array}{c}
n \
k
\end{array}\right) x^{n-k}(z-x)^{k} \
&=x^{n}+\sum_{k=0}^{n-1}\left(\begin{array}{c}
n \
k
\end{array}\right) x^{n-k}(z-x)^{k}=a+\sum_{k=0}^{n-1}\left(\begin{array}{c}
n \
k
\end{array}\right) x^{n-k}(z-x)^{k}>a .
\end{aligned}
$$
Turning the argument around, it is also not possible that $z<x$. Thus the $n^{\text {th }}$ root is also unique.
From now on, we will use this fact that $n^{t h}$ roots exist whenever it is convenient to do so.
$2.12$ Exercises
Let $S=[2,5]$. Find sup $S$. Now let $S=[2,5)$. Find sup $S$. Is sup $S$ always a number in $S$ ? Give conditions under which $\sup S \in S$ and then give conditions under which inf $S \in S$.
Show that if $S \neq \emptyset$ and is bounded sbove (below) then sup $S$ (inf $S$ ) is unique. That is, there is only one least upper bound and only one greatest lower bound. If $S=\emptyset$ can you conclude that 7 is an upper bound? Can you conclude 7 is a lower bound? What sbout $13.5 ?$ What about any other number?
Let $S$ be a set which is bounded sbove and let $-S$ denote the set ${-x: x \in S}$. How are inf $(-S)$ and sup $(S)$ related? Hint: Draw some pictures on a number line. What about sup $(-S)$ and inf $S$ where $S$ is a set which is bounded below?

其中，如所示，$C=\sum_{k=0}^{n-1}\left(\begin{array}{c}n \\ k\end{array}\right)|x|^{k }$。令 $\delta$ 足够小，使得右边小于 $\left|x^{n}-a\right|$。例如，你可以让 $\delta=\min \left(\frac{\left|x^{n}-a\right|}{2 C}, 1\right)$。那么如果 $y \in(x-\delta, x+\delta)$ $$ \left|y^{n}-x^{n}\right| \leq C|x-y|0$ 并令 $n>1$。那么存在一个唯一的$x>0$，使得$x^{n}=a$。证明：令$S$ 表示那些数$y \geq 0$ 使得$t^{n}-aa$，因此，在这种情况下，$S$ 以$a$ 为界。如果 $aa$，因此 $S$ 以 $1 / a$ 为界。通过完整性，存在$x$，$S$ 的最小上界。因此对于所有$y \leq x，y^{n}-a0$，那么根据引理，$y^{n}-a>0$ 在某个区间 $(x-\delta, x+\delta)$ 上。因此 $x$ 不能成为最小上界，因为上限是 $x-\delta / 2$。如果 $x^{n}-ax$，则由二项式定理， $$ \开始{对齐} z^{n} &=(x+z-x)^{n}=\sum_{k=0}^{n}\left(\begin{array}{c} n \\ ķ \end{数组}\right) x^{n-k}(z-x)^{k} \\ &=x^{n}+\sum_{k=0}^{n-1}\left(\begin{array}{c} n \\ ķ \end{array}\right) x^{n-k}(z-x)^{k}=a+\sum_{k=0}^{n-1}\left(\begin{array}{c} n \\ ķ \end{array}\right) x^{n-k}(z-x)^{k}>a 。 \end{对齐} $$ 反过来说，$z

real analysis代写analysis 2, analysis 3请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

代写隐藏