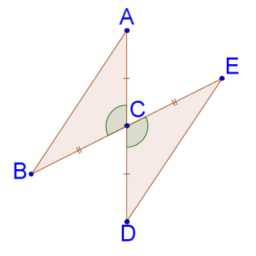
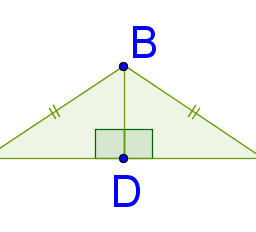
| Then for $t$ a real number, $$ \begin{gathered} 0 \leq p(t) \equiv \sum_{j=1}^{P}\left(z_{j}+t \theta w_{j}\right)\left(\overline{z_{j}}+t \overline{\theta w_{j}}\right) \ =\overbrace{\sum_{j=1}^{p} z_{j} \overline{z_{j}}}^{p}+\sum_{j=1}^{P} z_{j} t \overline{\theta \omega_{j}}+\sum_{j=1}^{P} t \theta w_{j} \overline{z_{j}}+t^{2} \sum_{j=1}^{P} w_{j} \overline{w_{j}} \ \equiv a^{2}+2 t \operatorname{Re} \theta \sum_{j=1}^{p} w_{j} \overline{z_{j}}+t^{2} b^{2}=a^{2}+2 t\left|\sum_{j=1}^{P} w_{j} \overline{z_{j}}\right|+t^{2} b^{2} \end{gathered} $$ Since this is always nonnegative for all real $t$, it follows from the quadratic formula that $$ 4\left|\sum_{j=1}^{P} w_{j} \overline{z_{j}}\right|^{2}-4 a^{2} b^{2}=4\left|\sum_{j=1}^{P} w_{j} \overline{z_{j}}\right|^{2}-4\left(\sum_{j=1}^{P} z_{j} \overline{z_{j}}\right)\left(\sum_{j=1}^{P} w_{j} \overline{w_{j}}\right) \leq 0 $$ Indeed, $p(t)=0$ either has exactly one real root or no real roots. Thus the desired inequality follows. 2.16 Integer Multiples of Irrational Numbers This section will give a proof of a remarkable result. I think its proof, based on the pigeon hole principle, is even more interesting than the result obtained. Dirichlet proved it in the 1830 ‘s. Jacobi used similar ideas around the same time in studying elliptic functions. The theorem involves the sum of integer multiples of numbers whose ratio is irrational. If $a / b$ is irrational, then it is not possible that $m a+n b=0, m, m \in \mathbb{Z}$ because if this were so, you would have $\frac{-m}{n}=\frac{b}{a}$ and so the ratio of $a, b$ is rational after all. Even though you cannot get 0 (which you can get if the ratio of $a$ and $b$ is rational) you can get such an integer combination arbitrarily small. Dirichlet did this in the 1830 ‘s long before the real numbers were constructed from the rational numbers in 1858 and published in 1872 . Theorem $2.16 .1$ If $a, b$ are real numbers and $a / b$ is not rational, then for every $\varepsilon>0$ there exist integers $m, n$ such that $|m a+n b|<\varepsilon$. Proof: Let $P_{N}$ denote all combinations of the form $m a+n b$ where $m, n$ are integers and $|m|,|n| \leq N$. Thus there are $(2 N+1)^{2}$ of these integer combinations and all of them are contained in the interval $I \equiv[-N(|a|+|b|), N(|a|+|b|)]$. Now pick an integer $M$ such that $$ (2 N)^{2}2$. Now partition the interval $I$ into $M$ equal intervals. If $l$ is the length of one of these intervals, then $$ \begin{aligned} l M &=2 N(|a|+|b|), \ l &=\frac{2 N(|a|+|b|)}{M}<\frac{2 N(|a|+|b|)}{(2 N)^{2}}=\frac{2(|a|+|b|)}{4} \frac{1}{N} \equiv \frac{C}{N} \end{aligned} $$ Now as mentioned, all of the points of $P_{N}$ are contained in $I$ and there are more of these points than there are intervals in the partition of $I$ which has only $M$ intervals. |

real analysis代写analysis 2, analysis 3请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
代写
隐藏