如果你也在 怎样代写流体力学Fluid Dynamics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。流体力学Fluid Dynamics“应用科学的一个分支,涉及到液体和气体的运动”。流体动力学是流体力学的两个分支之一,而流体力学是研究流体以及力如何影响它们。
流体力学Fluid Dynamics在物理学和工程学中,流体动力学是流体力学的一门分支学科,描述流体–液体和气体的流动。它有几个分支学科,包括空气动力学(研究空气和其他气体的运动)和流体动力学(研究液体的运动)。流体动力学有广泛的应用,包括计算飞机上的力和力矩,确定石油在管道中的质量流速,预测天气模式,了解星际空间的星云和建立裂变武器爆炸的模型。
my-assignmentexpert™流体力学Fluid Dynamics代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的流体力学Fluid Dynamics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此流体力学Fluid Dynamics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的作业代写服务。我们的专家在流体力学Fluid Dynamics代写方面经验极为丰富,各种流体力学Fluid Dynamics相关的作业也就用不着 说。
我们提供的流体力学Fluid Dynamics及其相关学科的代写,服务范围广, 其中包括但不限于:
美国代写|流体力学代写Fluid Dynamics代写|What is the Mechanical Definition of a Fluid?
The answer to this question may seem trivially obvious, but it turns out to be worth pondering. The term fluid encompasses both liquids and gases, the former being characterized by the existence of a free surface and the latter by the ease with which it may be compressed. Somewhat surprisingly, the macroscopic dynamics of both liquids and gases can be accounted for by more or less the same theory, with only modest differences in emphasis.
To construct such a theory we adopt the continuum approximation, which assumes that matter is smeared continuously across space. This approximation rests on the large difference between the molecular scale (the distance between molecules) and the characteristic distance over which the macroscopic properties of a fluid, such as density or pressure, vary. So, for example, the density of a fluid is defined as the mass per unit volume measured over a scale which is large enough for all molecular fluctuations to be smoothed out, yet small enough for the density, $\rho$, to be considered a smoothly varying function of position. Likewise, the stresses exerted by one part of a fluid on another are considered to be a smooth function of position, being defined as the force per unit area transmitted across a small plane surface within the fluid, the surface being infinitesimally small on the macroscopic scale, yet large on the molecular scale. These may be normal stresses, arising from forces perpendicular to the surface in question, or shear stresses, arising from tangential forces.
The distinction between solids and fluids is, at first sight, rather obvious; i.e. solids exhibit rigidity, while fluids readily deform when acted upon by a force. However, there are subtleties in this distinction that are worth noting. For example, we cannot distinguish between solids and liquids if only normal stresses are in play. Rather, it is the way in which these two states respond to an imposed shear stress that distinguishes between the two. Suppose, for example, that we have two cylinders, each sealed by a movable piston. One cylinder is filled with oil and the other with a cylindrical block of rubber. We now pressurize the contents of the two cylinders using the pistons. Evidently both systems behave in exactly the same way: when a compressive stress is imposed by the pistons, both the oil and the rubber compress a little, and then return to a state of static equilibrium.
美国代写|流体力学代写Fluid Dynamics代写|Fluid Statics and One Definition of Pressure
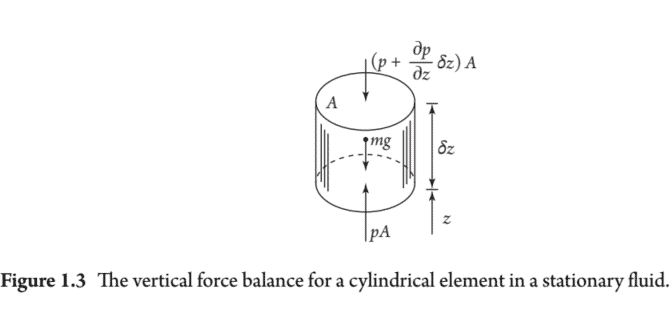
Before discussing the dynamics of fluids, perhaps it is worth making a few comments about hydrostatics, if only to reinforce the notions of pressure and of stresses acting within a fluid. Let us start with Pascal’s law for stationary fluids.
We have already seen that shear stresses are everywhere zero in a stationary fluid. Pascal’s law follows directly from this and states that the magnitude of the normal stress acting at any given point is independent of direction. The proof is trivial. Let us use $\sigma$ to denote a normal stress and reserve $\tau$ for shear stress. Consider a small wedge of fluid of mass $m$ surrounding the point of interest, as shown in Figure 1.2. Let the wedge have sides $\delta x, \delta y$, and $\delta z$, and let $\sigma_{x}, \sigma_{z}$, and $\sigma_{\alpha}$ be the normal stresses in the $x$ and $z$ directions and on the inclined surface. As there are no shear stresses, vertical equilibrium demands
$$
\left[\sigma_{\alpha}(\delta L \delta y)\right] \cos \alpha=\sigma_{\alpha}(\delta x \delta y)=\sigma_{z}(\delta x \delta y)+\rho g\left(\frac{1}{2} \delta x \delta y \delta z\right)
$$
and as the size of the wedge tends to zero the weight $m g$ drops out of (1.2) to give $\sigma_{\alpha}=\sigma_{z}$. Similarly, horizontal equilibrium requires $\sigma_{\alpha}=\sigma_{x}$. So, we conclude that because of the absence of shear stress, the normal stress, $\sigma$, is the same in all directions. In fluid dynamics the normal stresses are compressive, and so we define the fluid pressure to be $p=-\sigma$, and Pascal’s law is sometimes paraphrased as saying that the pressure at any given point is the same in all directions
美国代写|流体力学代写FLUID DYNAMICS代写|Different Categories of Fluid and of Fluid Flow
We now turn to dynamics. Before presenting a formal analysis of fluids in motion, it is, perhaps, useful to discuss the different approximations commonly employed in fluid dynamics, as well as the different regimes of behaviour normally encountered in practice. Perhaps the first important subdivision is between incompressible and compressible flows. It is tempting to associate the former with liquids and the latter with gases, but this is too simplistic. Compressibility cannot always be ignored in liquids (think of acoustic waves in the oceans), and, conversely, gasses in which the Mach number (the flow speed divided by the speed of sound) is less than $0.3$ usually exhibit negligible variation in density. In this text we consider only incompressible flows.
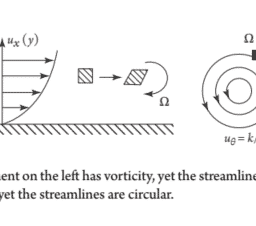
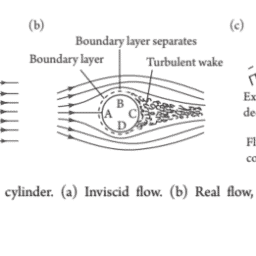
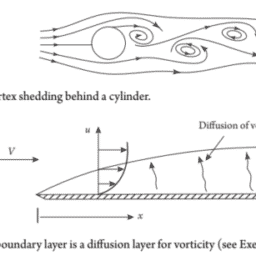
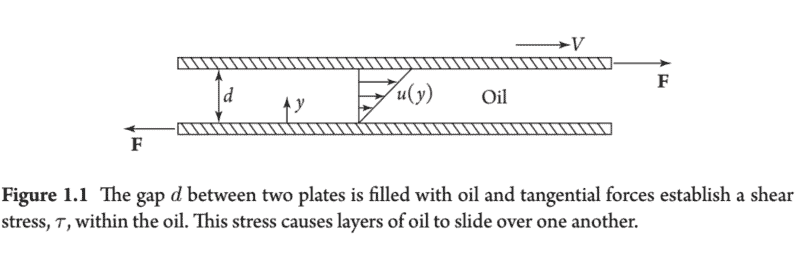
The second subdivision is between ideal and real fluids. As mentioned above, it is sometimes convenient to ignore the viscous stresses in a fluid on the grounds that the viscosity, which is always finite, is sufficiently small for those stresses to be negligible. A hypothetical fluid with zero viscosity is called an ideal fluid. Real fluids stick to solid surfaces (Figure 1.1), whereas an ideal fluid is free to slip over such a surface. Moreover, viscous stresses convert mechanical energy into heat, whereas ideal fluids conserve mechanical energy (in the absence of external forces). So, an inviscid fluid can be a useful idealization, but one that invariably breaks down near solid surfaces in motion.
流体力学代写
美国代写|流体力学代写FLUID DYNAMICS代写|WHAT IS THE MECHANICAL DEFINITION OF A FLUID?
这个问题的答案看似微不足道,但结果却值得深思。术语流体包括液体和气体,前者的特征在于存在自由表面,而后者的特征在于它可以容易地被压缩。有点令人惊讶的是,液体和气体的宏观动力学可以用或多或少相同的理论来解释,只是在重点上略有不同。
为了构建这样一个理论,我们采用了连续近似,它假设物质在空间中被连续涂抹。这种近似基于分子尺度之间的巨大差异吨H和d一世s吨一个nC和b和吨在和和n米○l和C在l和s以及流体的宏观特性(例如密度或压力)变化的特征距离。因此,例如,流体的密度被定义为在一个尺度上测量的每单位体积的质量,该尺度足够大,可以消除所有分子波动,但又足够小,可以消除密度,ρ,被认为是位置的平滑变化函数。同样,流体的一部分施加在另一部分上的应力被认为是位置的平滑函数,定义为通过流体内的小平面表面传输的每单位面积的力,该表面在宏观尺度上无限小,但在分子尺度上很大。这些可能是由垂直于所讨论表面的力产生的法向应力,或由切向力产生的剪应力。
乍一看,固体和液体之间的区别相当明显。即固体表现出刚性,而流体在受力作用时容易变形。然而,这种区别中有一些微妙之处值得注意。例如,如果只有法向应力起作用,我们就无法区分固体和液体。相反,正是这两种状态对施加的剪应力做出反应的方式将两者区分开来。例如,假设我们有两个气缸,每个气缸都由一个可移动的活塞密封。一个圆柱体充满油,另一个圆柱体充满橡胶块。我们现在使用活塞对两个气缸的内容物进行加压。显然,这两个系统的行为方式完全相同:当活塞施加压缩应力时,油和橡胶都会压缩一点,
美国代写|流体力学代写FLUID DYNAMICS代写|FLUID STATICS AND ONE DEFINITION OF PRESSURE
在讨论流体动力学之前,也许有必要对流体静力学做一些评论,如果只是为了加强压力和作用于流体内的应力的概念。让我们从静态流体的帕斯卡定律开始。
我们已经看到,在静止流体中,剪切应力处处为零。帕斯卡定律直接由此得出,并指出作用在任何给定点的法向应力的大小与方向无关。证明是微不足道的。让我们使用σ表示正常压力和储备τ为剪应力。考虑一小块有质量的流体米围绕兴趣点,如图 1.2 所示。让楔子有边dX,d是, 和d和, 然后让σX,σ和, 和σ一个是正应力X和和方向和斜面上。由于没有剪切应力,因此需要垂直平衡
[σ一个(d大号d是)]因一个=σ一个(dXd是)=σ和(dXd是)+ρG(12dXd是d和)
并且随着楔子的大小趋向于零重量米G掉出1.2给予σ一个=σ和. 同样,水平平衡需要σ一个=σX. 因此,我们得出结论,由于没有剪应力,法向应力,σ, 在所有方向上都是相同的。在流体动力学中,法向应力是压缩的,因此我们将流体压力定义为p=−σ, 帕斯卡定律有时被解释为任何给定点的压力在所有方向上都是相同的
美国代写|流体力学代写FLUID DYNAMICS代写|DIFFERENT CATEGORIES OF FLUID AND OF FLUID FLOW
我们现在转向动力学。在对运动中的流体进行正式分析之前,讨论流体动力学中常用的不同近似值以及实践中通常遇到的不同行为方式也许是有用的。也许第一个重要的细分是在不可压缩流和可压缩流之间。将前者与液体联系起来,将后者与气体联系起来是很诱人的,但这太简单了。在液体中不能总是忽略可压缩性吨H一世nķ○F一个C○在s吨一世C在一个在和s一世n吨H和○C和一个ns, 和相反的,其中马赫数为吨H和Fl○在sp和和dd一世在一世d和db是吨H和sp和和d○Fs○在nd小于0.3通常表现出可忽略不计的密度变化。在本文中,我们只考虑不可压缩的流动。
第二个细分介于理想流体和真实流体之间。如上所述,有时忽略流体中的粘性应力是很方便的,因为粘性总是有限的,足够小,可以忽略不计。粘度为零的假设流体称为理想流体。真正的流体粘附在固体表面F一世G在r和1.1,而理想流体可以在这样的表面上自由滑动。此外,粘性应力将机械能转化为热能,而理想流体保存机械能一世n吨H和一个bs和nC和○F和X吨和rn一个lF○rC和s. 因此,无粘性流体可能是一种有用的理想化,但它总是会在运动中的固体表面附近分解。

美国代写|流体力学代写Fluid Dynamics代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。