如果你也在 怎样代写Matlab EMET3007/8012学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。Matlab是一个编程和数值计算平台,被数百万工程师和科学家用来分析数据、开发算法和创建模型。
时间序列分析(Time-Series Analysis)是指将原来的销售分解为四部分来看——趋势、周期、时期和不稳定因素,然后综合这些因素,提出销售预测。 强调的是通过对一个区域进行一定时间段内的连续遥感观测,提取图像有关特征,并分析其变化过程与发展规模。
代写Matlab,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的代写Matlab作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此代写Matlab作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在数学Mathematics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的时间序列分析(Time-Series Analysis)代写服务。我们的专家在时间序列分析(Time-Series Analysis)代写方面经验极为丰富,各种时间序列分析(Time-Series Analysis)相关的作业也就用不着 说。
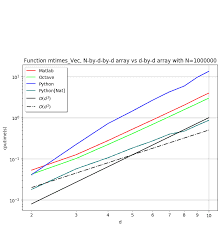
这是一份2022年的 Australian National University澳洲国立大学EMET3007/8012作业代写的成功案例
EMET3007/8012 Assignment 2
Instructions: This assignment is worth either 20% or 25% of the final grade, and is worth a total of 75 points. All working must be shown for all questions. For questions which ask you to write a program, you must provid the code you used. If you have found code and then modified it, then the original source must be cited. The assignment is due by 5pm Friday 1st of October (Friday of Week 8), using Turnitin on Wattle. Late submissions will only be accepted with prior written approval. Good luck.

[10 marks] In this exercise we will consider four different specifications for forecasting monthly Australian total employed persons. The dataset (available on Wattle) AUSEmp 1oy 2022. csv contains three columns; the first column contains the date; the second contains the sales figures for that month (FRED data series LFEMTTTTAUM647N), and the third contains Australian GDP for that month.1] The data runs from January 1995 to January $2022 .$
Let $M_{i t}$ be a dummy variable that denotes the month of the year. Let $D_{i t}$ be a dummy variable which denotes the quarter of the year. The four specifications we consider are
$$
\begin{aligned}
&S_1: y_t=a_0+a_1 t+\alpha_4 D_{4 t}+\epsilon_t \
&S_2: y_t=a_1 t+\sum_{i=1}^4 \alpha_i D_{i t}+\epsilon_t \
&S_3: y_t=a_0+a_1 t+\beta_{12} M_{12, t}+\epsilon_t \
&S_4: y_t=a_1 t+\sum_{i=1}^{12} \beta_i M_{i t}+\epsilon_t
\end{aligned}
$$
where $\mathbb{E} \epsilon_t=0$ for all $t$.
a) For each specification, describe this specification in words.
b) For each specification, estimate the values of the parameters, and compute the MSE, $\mathrm{AIC}$, and BIC. If you make any changes to the csv file, please describe the changes you make. As always, you must include your code.
c) For each specification, compute the MSFE for the 1-step and 5-step ahead forecasts, with the out-of-sample forecasting exercise beginning at $T_0=50$.
d) For each specification, plot the out-of-sample forecasts and comment on the results.
[10 marks] Now add to Question 1 the additional assumption that $\epsilon_t \sim \mathcal{N}\left(0, \sigma^2\right)$. One estimator ${ }^2$ for $\sigma^2$ is
$$
\hat{\sigma}^2=\frac{1}{T-k} \sum_{t=1}^T\left(y_t-\hat{y}_t\right)^2
$$
where $\hat{y}_t$ is the estimated value of $y_t$ in the model and $k$ is the number of regressors in the specification.
a) For each specification $\left(S_1, \ldots, S_4\right)$, compute $\hat{\sigma}^2$.
b) For each specification, make a $95 \%$ probability forecast for the sales in June $2021 .$
c) For each specification, compute the probability that the total employed persons in June 2022 will be greater than $13.5$ million. According to the FRED series LFEMTTTTAUM647N, what was the actual employment level for that month.
d) Do you think the assumption that $\epsilon_t$ is iid is a reasonable assumption for this data series.
[10 marks] Here we investigate whether adding GDP $\mathrm{Gs}^3$ as a predictor can improve our forecasts. Consider the following modified specifications:
$$
\begin{aligned}
&S_1^{\prime}: y_t=a_0+a_1 t+\alpha_4 D_{4 t}+\gamma x_{t-h}+\epsilon_t \
&S_2^{\prime}: y_t=a_1 t+\sum_{i=1}^4 \alpha_i D_{i t}+\gamma x_{t-h}+\epsilon_t \
&S_3^{\prime}: y_t=a_0+a_1 t+\beta_{12} M_{12, t}+\gamma x_{t-h}+\epsilon_t \
&S_4^{\prime}: y_t=a_1 t+\sum_{i=1}^{12} \beta_i M_{i t}+\gamma x_{t-h}+\epsilon_t
\end{aligned}
$$
where $\mathbb{E} \epsilon_t=0$ for all $t$, and $x_{t-h}$ is GDP at time $t-h$. For each specification, compute the MSFE for the 1-step ahead, and the 5-step ahead forecasts, with the out-of-sample forecasting exercise beginning at $T_0=50$. For each specification, plot the out-of-sample forecasts and comment on the results.
[15 marks] Here we investigate whether Holt-Winters smoothing can improve our forecasts. Use a Holt-Winters smoothing method with seasonality, to produce 1-step ahead and 5-step ahead forecasts and compute the MSFE for these forecasts. You should use smoothing parameters $\alpha=\beta=\gamma=0.3$ and start the out-of-sample forecasting exercise at $T_0=50$. Plot these out-of-sample forecasts and comment on the results.
Additionally, estimate the values for $\alpha, \beta$, and $\gamma$ which minimise the MSFE. Find the MSFE for these parameter vales and compare it to the baseline $\alpha=\beta=\gamma=0.3$.
[10 marks] Develop another model, either based on material from class or otherwise, to forecast Australian Total Employment. Your new model should perform better (have a lower MSFE or MAFE) than all models from Questions 1,3, and 4. As part of your response to this question you must provide:
a) a brief written explanation of what your model is doing,
b) a brief statement on why you think your new model will perform better,
c) any relevant equations or mathematics/statistics to describe the model,
d) the code to run the model, and
e) the MSFE and/or MAFE error found by your model, and a brief discussion of how this compares to previous cases.
[15 marks] Consider the ARX(1) model
$$
y_t=\mu+a t+\rho y_{t-1}+\epsilon_t
$$
where the errors follow an $\mathrm{AR}(2)$ process
$$
\epsilon_t=\phi_1 \epsilon_{t-1}+\phi_2 \epsilon_{t-2}+u_t, \quad \mathbf{u} \sim \mathcal{N}\left(0, \sigma^2 I\right)
$$
for $t=1, \ldots, T$ and $e_{-1}=e_0=0$. Suppose $\phi_1, \phi_2$ are known. Find (analytically) the maximum likelihood estimators for $\mu, a, \rho$, and $\sigma^2$.
Hint: First write $y$ and $\epsilon$ in vector/matrix form. You may wish to use different looking forms for each. Find the distribution of $\epsilon$ and $y$. Then apply some appropriate calculus. You may want to let $H=I-\phi_1 L-\phi_2 L^2$, where $I$ is the $T \times T$ identity matrix, and $L$ is the lag matrix.

matlab代写不如考虑my-assignmentexpert™!. my-assignmentexpert™为您的留学生涯保驾护航。

