博弈论代写代考| Dominant Strategies and Nash Equilibrium Points 数学代写
博弈论代考
In this section, we begin our study of how to solve games. To illustrate the two main ideas introduced in this section, we draw upon an actual episode from World War II, the Battle of the Bismarck Sea. The episode lends itself well to game theoretic analysis, as was shown originally by O. G. Haywood, Jr., who published an article about this battle in the Journal of Operations Research in 1954. Since then, it has been discussed in a number of texts, including Luce and Raiffa (1957), Dixit and Skeath (1999), and Casti (1996).
The situation was this: In 1943, the island of New Guinea was divided between Japanese forces (who controlled the northern half) and the Allied forces (who controlled the southern half). New Guinea is the world’s second-largest island (after Greenland) and is located roughly between Australia and the island of New Britain, with the Bismarck Sea to the north of
A Japanese convoy was being assembled at their base in Rabaul on New Britain. Between February 7 and February 14, Allied forces began to detect the preparations of the Japanese forces at Raboul, but they did not know the destination of the convoy. On February 16 , codebreakers in Melbourne, Australia, and Washington, DC, decrypted a Japanese message that indicated that convoys were being planned for three different destinations, with the Japanese base at Lae, New Guinea, being one of them. Subsequently, a message from the Japanese 11th Air Fleet was intercepted, indicating that destroyers and six transports would land at Lae around March 5. (Later, earlier date.)
Since Raboul is at the northeast tip of New Britain, the convoy would have to sail around the entire island of New Britain to land in New Guinea, which is near the southwest end of New Britain. They could sail north of New Britain, in the Bismarck Sea, or south of New Britain, in the Solomon Sea. New Britain itself is fairly large – the largest island of the Bismarck Archipelago, and either route would entail a trip of three days. The Allied forces, led by Lieutenant General General Douglas MacArthur, decided to attack the convoy as it sailed.
The pouglas MacArthur, decided to attack the convoy as it sailed. journey and inflict as much damage as possible to the convoy before it reached Lae. But the Allied
6.2 Dominant Strategies and Nash Equilibrium Points 253
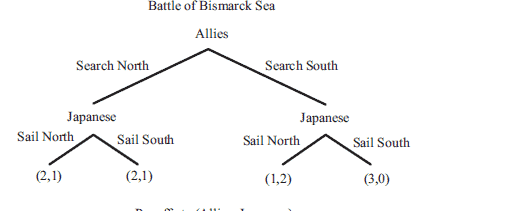
在本节中,我们开始研究如何解决博弈。为了说明本节介绍的两个主要思想,我们借鉴了二战中的一个真实事件,即俾斯麦海海战。这一集很适合博弈论分析,正如 OG Haywood, Jr. 最初所展示的那样,他于 1954 年在《运筹学杂志》上发表了一篇关于这场战斗的文章。从那时起,它已经在许多文本中进行了讨论,包括 Luce 和 Raiffa (1957)、Dixit 和 Skeath (1999) 和 Casti (1996)。
情况是这样的:1943 年,新几内亚岛被日军(控制北半部)和盟军(控制南半部)瓜分。新几内亚是世界第二大岛(仅次于格陵兰岛),大致位于澳大利亚和新不列颠岛之间,北濒俾斯麦海
一支日本车队正在新不列颠的拉包尔基地集结。 2月7日至2月14日,盟军开始侦查日军在拉布尔的准备情况,但不知道车队的目的地。 2 月 16 日,澳大利亚墨尔本和华盛顿特区的密码破译者解密了一条日本消息,该消息表明车队正计划前往三个不同的目的地,新几内亚莱城的日本基地就是其中之一。随后,截获了来自日本第 11 航空舰队的一条消息,表明驱逐舰和 6 艘运输舰将于 3 月 5 日左右在莱城登陆。(后来,更早的日期。)
由于拉布尔位于新不列颠的东北端,车队必须绕着整个新不列颠岛航行,才能在靠近新不列颠西南端的新几内亚登陆。他们可以在新不列颠以北的俾斯麦海或新不列颠以南的所罗门海航行。新不列颠本身相当大——俾斯麦群岛最大的岛屿,任何一条路线都需要三天的行程。由道格拉斯麦克阿瑟中将率领的盟军决定在车队航行时对其进行攻击。
pouglas MacArthur 决定在车队航行时攻击它。并在车队到达莱城之前对车队造成尽可能多的伤害。但盟军
6.2 优势策略和纳什均衡点 253
博弈论代写
博弈论是关于什么的?当我妻子外出参加托斯卡纳的一个愉快的小型会议时,三位年轻女性邀请我与她们同桌共进午餐。当我坐下时,其中一个用闷热的声音说,“教我们如何玩爱情游戏”,但事实证明,他们想要的只是关于如何管理意大利男朋友的建议。我仍然认为他们拒绝我的战略建议是错误的,但他们正确地认为求爱是我们在现实生活中玩的许多不同类型的游戏之一在交通繁忙的司机正在玩驾驶游戏。在 eBay 上竞标的讨价还价者正在玩拍卖游戏。一家公司和一个工会正在谈判明年的工资,这是一场讨价还价的游戏。当反对的候选人在选举中选择他们的平台时,他们正在玩一场政治游戏。决定今天玉米片价格的杂货店老板正在玩一场经济游戏。简而言之,每当人类互动时,就会玩游戏。
每次新的巨额电信拍卖都需要根据将要运行的环境进行调整。不能像美国政府在聘请苏富比拍卖一堆卫星转发器时发现的那样,将设计从货架上拿下来。但也无法在数学模型中捕捉到新电信市场的所有复杂细节。因此,设计电信拍卖既是一门艺术,也是一门科学。一个人从简单的模型中推断出来,这些模型被选择来模仿似乎是问题的基本战略特征。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
博弈论,又称为对策论(Game Theory)、赛局理论等,既是现代数学的一个新分支,也是运筹学的一个重要学科。 博弈论主要研究公式化了的激励结构间的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法。 博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。