博弈论代写代考| Variable-Sum Games 数学代写
博弈论代考
With constant-sum games, we introduced mixed strategies as a way to handle games that were not strictly determined; that is, they had no saddle points, which were the same things as pure strategy Nash equilibria. The same idea works for variable-sum games. It is quite possible that a variable-sum game has no pure-strategy Nash equilibrium. Yet Nash proved that every game has at least one equilibrium point, so there must be a way to find one using mixed strategies. We’ll show an example presently, but before embarking on the example, we caution the reader not to get his or her hopes up too much. In the example of the last subsection, we did find a Nash equilibrium (even one using pure strategies), yet we had reason to possibly reject that outcome as an alleged “solution” to the game.
Consider the game with the following payoff matrix:
$$
A=\left[\begin{array}{ll}
(3,5) & (6,1) \
(7,2) & (5,7)
\end{array}\right]
$$
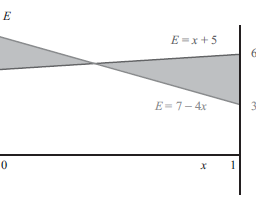
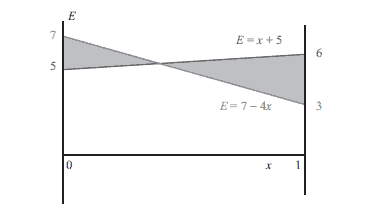
The reader should check that none of the four outcomes is a Nash equilibrium (for example, draw a movement diagram). The concept of a mixed strategy is the same as before, as is the notation. Thus, playing $p=[0.4,0.6]$ can be interpreted as playing the first row $40 \%$ of the time in the long run with repeated play or, equally well, as saying that on any one play of the game, the first row is played with probability $0.4$. So, for example, if $p=[0.4,0.6]$ and $q=\left[\begin{array}{l}0.7 \ 0.3\end{array}\right]$, how do we determine the expected payoff to each player? The formula $E(p, q)=p A q$ is still valid (assuming that the players choose simultaneously and independently, as usual), only this time, we must be careful about what we use for $A$. If you want the row players payoffs, you use just the first coordinates in the payoffs in A. To obtain the column players payoffs, in the constant-sum case, this time using the second coordinates in $A$. So for the given example:
对于恒和博弈,我们引入了混合策略来处理非严格确定的博弈;也就是说,它们没有鞍点,这与纯策略纳什均衡相同。同样的想法也适用于可变和游戏。可变和博弈很可能没有纯策略纳什均衡。然而,纳什证明了每场博弈至少有一个平衡点,因此必须有一种方法可以使用混合策略找到一个平衡点。我们现在将展示一个示例,但在开始示例之前,我们提醒读者不要抱太大希望。在上一小节的示例中,我们确实找到了一个纳什均衡(即使是使用纯策略的均衡),但我们有理由可能拒绝将该结果作为所谓的博弈“解决方案”。
考虑具有以下收益矩阵的博弈:
$$
A=\left[\begin{数组}{ll}
(3,5) & (6,1) \
(7,2) & (5,7)
\end{数组}\right]
$$
读者应该检查四个结果中没有一个是纳什均衡(例如,画一个运动图)。混合策略的概念与之前相同,符号也相同。因此,玩 $p=[0.4,0.6]$ 可以解释为从长远来看重复玩第一行 $40 \%$ 的时间,或者同样好,说在任何一次游戏中,第一行以 0.4 美元的概率播放。因此,例如,如果 $p=[0.4,0.6]$ 和 $q=\left[\begin{array}{l}0.7 \ 0.3\end{array}\right]$,我们如何确定预期给每个玩家的回报?公式 $E(p, q)=p A q$ 仍然有效(假设玩家像往常一样同时独立选择),只是这一次,我们必须小心我们对 $A$ 的使用。如果您想要行玩家收益,您只使用 A 中收益中的第一个坐标。为了获得列玩家收益,在恒定和的情况下,这次使用 $A$ 中的第二个坐标。所以对于给定的例子:
博弈论代写
博弈论是关于什么的?当我妻子外出参加托斯卡纳的一个愉快的小型会议时,三位年轻女性邀请我与她们同桌共进午餐。当我坐下时,其中一个用闷热的声音说,“教我们如何玩爱情游戏”,但事实证明,他们想要的只是关于如何管理意大利男朋友的建议。我仍然认为他们拒绝我的战略建议是错误的,但他们正确地认为求爱是我们在现实生活中玩的许多不同类型的游戏之一在交通繁忙的司机正在玩驾驶游戏。在 eBay 上竞标的讨价还价者正在玩拍卖游戏。一家公司和一个工会正在谈判明年的工资,这是一场讨价还价的游戏。当反对的候选人在选举中选择他们的平台时,他们正在玩一场政治游戏。决定今天玉米片价格的杂货店老板正在玩一场经济游戏。简而言之,每当人类互动时,就会玩游戏。
每次新的巨额电信拍卖都需要根据将要运行的环境进行调整。不能像美国政府在聘请苏富比拍卖一堆卫星转发器时发现的那样,将设计从货架上拿下来。但也无法在数学模型中捕捉到新电信市场的所有复杂细节。因此,设计电信拍卖既是一门艺术,也是一门科学。一个人从简单的模型中推断出来,这些模型被选择来模仿似乎是问题的基本战略特征。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
博弈论,又称为对策论(Game Theory)、赛局理论等,既是现代数学的一个新分支,也是运筹学的一个重要学科。 博弈论主要研究公式化了的激励结构间的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法。 博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。