美国数学邀请赛是一项面向中学生的数学竞赛,起始于1983年。该竞赛有15道问题,考试时间为3小时。AMC10前2.5%和AMC12前5%的学生有资格参加美国数学邀请赛。和美国数学竞赛、美国数学奥林匹克共同作为选拔国际数学奥林匹克美国队的赛事,该赛事处于选拔的第二级,胜出者方能参加下一级的美国数学奥林匹克比赛。
AIME资格认证的变化
从2011年开始,美国数学邀请考试(AIME)的资格参数将略有放宽。对于参加2012年AMC 10竞赛的学生,我们将邀请所有得分最高的2.5%的学生或得分至少为120分的学生(以更多的为准)参加AIME。这与2004年以来一直实行的1%(或120分)的数值不同。对于参加2012年AMC 12的学生,我们将邀请所有得分者中的前5%或得分者中至少有100分的学生参加AIME。这些AMC 12的资格值保持在2000年以来的水平。这一政策是为了防止出现特别困难的考试,即分数一致低于正常水平的考试,从而减少AIME的合格人数。
对AMC 10名合格者设定较高的要求有两个原因。
- 首先,AIME考试可能相当令人生畏,我们不希望年轻学生因考试成绩不佳而气馁。
- 第二,我们希望确保任何通过AMC 10考试获得AIME资格的学生在随后几年参加AMC 12考试时也有可能获得AIME资格。如果一个学生在10年级获得了AIME资格,但在随后的高中阶段却没有,这可能会让人非常失望。
通过限制从AMC10年级获得AIME资格的人数为前2.5%,我们的计划是不排除任何非常优秀的年轻学生,对他们来说,AIME是一个适当的经验,但也不会让学生处于没有成功机会的情况。
请注意:AIME II(备用AIME)的新程序。
今年,AMC将对AIME II(也称为AIME候补)采用一些新的程序。回顾一下,AIME II的第二个(或备用)日期是 , , 。
AMC办公室将从2月下旬开始向学校邮寄2012年AMC 10和2012年AMC 12报告,并持续到3月初至3月中旬。 在该AMC 10和AMC 12报告中,将列出学校的AIME合格者名单。
报告中还包括该校AIME选手的AIME I竞赛(装在一个密封的信封里)、AIME答题表和AIME/USAMO教师手册。这与我们多年来的做法相同。
如果你的AIME合格者将在WWW考试时参加AIME I考试,那么一切都准备好了,你只需要按照《教师手册》中AIME I的指示,将AIME答卷寄回,以便评分。
如果你的AIME参赛者将在WWW上参加AIME II,那么你仍然需要在我们的网页上(电子注册)或AIME教师手册中的纸质表格上填写AIME II(或AIME备用)注册。请务必填写一个有效的电子邮件地址。
保存你在AMC10/AMC12报告中收到的AIME答案表。我们将在AIME I和AIME II中使用相同的答案表格。同时保存AIME报告信封,我们将使用同一个AIME报告信封寄回AIME I和AIME II。
请在3月28日关注您的电子邮件,查看包含AIME II的电子信息。它将以PDF文件的形式出现在邮件中。打印AIME II,然后为每个参加AIME II的合格者复印足够的副本。
让参加AIME II的学生用铅笔在答题表的正面上方写上 “AIME II”,与答案同侧。
任何其他必要的指示将在AIME教师手册中列出。
这些新的程序是为了降低成本,更快,更有效,更环保,减少纸张和运输。
认可
AIME的目的是在AMC10或AMC12之外,为北美许多具有特殊数学能力的高中生提供进一步的挑战和认可。得分最高的美国公民和合法居住在美国和加拿大的学生(根据加权平均分,获得合格分数)被邀请参加美国数学竞赛。
AIME(美国数学邀请考试)是介于AMC10或AMC12和USAMO之间的考试。所有参加AMC 12的学生,如果在可能的150分中取得100分或以上的成绩,或在前5%的学生被邀请参加AIME考试。所有参加AMC 10的学生,在可能的150分中取得120分或以上,或进入前2.5%的学生也有资格参加AIME。本学年AIME I的日期为 ,AIME II的日期为 , 。美国数学邀请考试没有额外的注册费,除非你选择参加第二次考试。额外的管理/运输费是要收取的,前10名学生的最低费用为,超过10名学生的最低费用为。这在AMC 10/12和AIME教师手册中有更详细的解释。
数学竞赛代考|AIME代考美国数学邀请赛|2022 AIME I Problems
Problem 1
Quadratic polynomials $P(x)$ and $Q(x)$ have leading coefficients 2 and $-2$, respectively. The graphs of both polynomials pass through the two points $(16,54)$ and $(20,53)$. Find $P(0)+Q(0)$.
Solution
Problem 2
Find the three-digit positive integer $a b c$ whose representation in base nine is $b c a_{\text {nine }}$, where $a, b$, and $c$ are (not necessarily distinct) digits.
Solution
Problem 3
In isosceles trapezoid $A B C D$, parallel bases $\overline{A B}$ and $\overline{C D}$ have lengths 500 and 650 , respectively, and $A D=B C=333$. The angle bisectors of $\angle A$ and $\angle D$ meet at $P$, and the angle bisectors of $\angle B$ and $\angle C$ meet at $Q$. Find $P Q$.
Solution
Problem 4
Let $w=\frac{\sqrt{3}+i}{2}$ and $z=\frac{-1+i \sqrt{3}}{2}$, where $i=\sqrt{-1}$. Find the number of ordered pairs $(r, s)$ of positive integers not exceeding 100 that satisfy the equation $i \cdot w^r=z^s$.
Solution
Problem 5
A straight river that is 264 meters wide flows from west to east at a rate of 14 meters per minute. Melanie and Sherry sit on the south bank of the river with Melanie a distance of $D$ meters downstream from Sherry. Relative to the water, Melanie swims at 80 meters per minute, and Sherry swims at 60 meters per minute. At the same time, Melanie and Sherry begin swimming in straight lines to a point on the north bank of the river that is equidistant from their starting positions. The two women arrive at this point simultaneously. Find $D$.
Solution
Problem 6
Find the number of ordered pairs of integers $(a, b)$ such that the sequence
$$
3,4,5, a, b, 30,40,50
$$
is strictly increasing and no set of four (not necessarily consecutive) terms forms an arithmetic progression.
Solution
Problem 7
Let $a, b, c, d, e, f, g, h, i$ be distinct integers from 1 to 9 . The minimum possible positive value of
$$
\frac{a \cdot b \cdot c-d \cdot e \cdot f}{g \cdot h \cdot i}
$$
can be written as $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.
Solution
Problem 8
Equilateral triangle $\triangle A B C$ is inscribed in circle $\omega$ with radius 18 . Circle $\omega_A$ is tangent to sides $\overline{A B}$ and $\overline{A C}$ and is internally tangent to $\omega$. Circles $\omega_B$ and $\omega_C$ are defined analogously. Circles $\omega_A, \omega_B$, and $\omega_C$ meet in six points–two points for each pair of circles. The three intersection points closest to the vertices of $\triangle A B C$ are the vertices of a large equilateral triangle in the interior of $\triangle A B C$, and the other three intersection points are the vertices of a smaller equilateral triangle in the interior of $\triangle A B C$. The side length of the smaller equilateral triangle can be written as $\sqrt{a}-\sqrt{b}$, where $a$ and $b$ are positive integers. Find $a+b$.
Solution
Problem 9
Ellina has twelve blocks, two each of red $(\mathbf{R})$, blue $(\mathbf{B})$, yellow $(\mathbf{Y})$, green $(\mathbf{G})$, orange $(\mathbf{O})$, and purple $(\mathbf{P})$. Call an arrangement of blocks even if there is an even number of blocks between each pair of blocks of the same color. For example, the arrangement
R B B Y G G Y R OPPO
is even. Ellina arranges her blocks in a row in random order. The probability that her arrangement is even is $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.
Solution
Problem 10
Three spheres with radii 11,13 , and 19 are mutually externally tangent. A plane intersects the spheres in three congruent circles centered at $A$, $B$, and $C$, respectively, and the centers of the spheres all lie on the same side of this plane. Suppose that $A B^2=560$. Find $A C^2$.
Solution
Problem 11
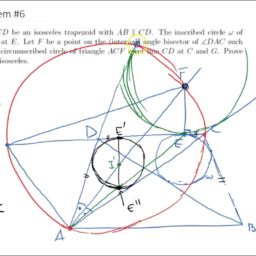
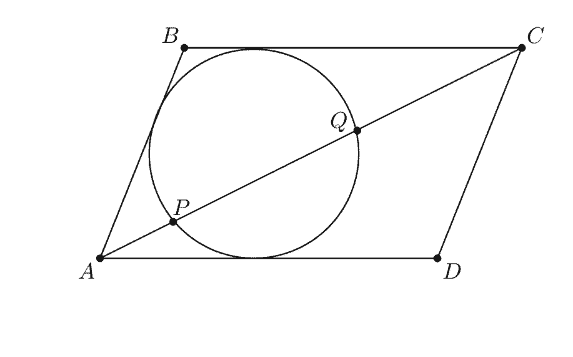
Let $A B C D$ be a parallelogram with $\angle B A D<90^{\circ}$. A circle tangent to sides $\overline{D A}, \overline{A B}$, and $\overline{B C}$ intersects diagonal $\overline{A C}$ at points $P$ and $Q$ with $A P<A Q$, as shown. Suppose that $A P=3, P Q=9$, and $Q C=16$. Then the area of $A B C D$ can be expressed in the form $m \sqrt{n}$, where $m$ and $n$ are positive integers, and $n$ is not divisible by the square of any prime. Find $m+n$.
Problem 12
For any finite set $X$, let $|X|$ denote the number of elements in $X$. Define
$$
S_n=\sum|A \cap B|,
$$
where the sum is taken over all ordered pairs $(A, B)$ such that $A$ and $B$ are subsets of ${1,2,3, \ldots, n}$ with $|A|=|B|$. For example, $S_2=4$ because the sum is taken over the pairs of subsets
$$
(A, B) \in{(\emptyset, \emptyset),({1},{1}),({1},{2}),({2},{1}),({2},{2}),({1,2},{1,2})},
$$
giving $S_2=0+1+0+0+1+2=4$. Let $\frac{S_{2022}}{S_{2021}}=\frac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find the remainder when $p+q$ is divided by 1000 .
Solution
Problem 13
Let $S$ be the set of all rational numbers that can be expressed as a repeating decimal in the form $0 . \overline{a b c d}$, where at least one of the digits $a, b, c$, or $d$ is nonzero. Let $N$ be the number of distinct numerators obtained when numbers in $S$ are written as fractions in lowest terms. For example, both 4 and 410 are counted among the distinct numerators for numbers in $S$ because $0 . \overline{3636}=\frac{4}{11}$ and $0 . \overline{1230}=\frac{410}{3333}$. Find the remainder when $N$ is divided by 1000 .
Solution
Problem 14
Given $\triangle A B C$ and a point $P$ on one of its sides, call line $\ell$ the splitting line of $\triangle A B C$ through $P$ if $\ell$ passes through $P$ and divides $\triangle A B C$ into two polygons of equal perimeter. Let $\triangle A B C$ be a triangle where $B C=219$ and $A B$ and $A C$ are positive integers. Let $M$ and $N$ be the midpoints of $\overline{A B}$ and $\overline{A C}$, respectively, and suppose that the splitting lines of $\triangle A B C$ through $M$ and $N$ intersect at $30^{\circ}$. Find the perimeter of $\triangle A B C$.
Solution
Problem 15
Let $x, y$, and $z$ be positive real numbers satisfying the system of equations:
$$
\begin{aligned}
\sqrt{2 x-x y}+\sqrt{2 y-x y} &=1 \
\sqrt{2 y-y z}+\sqrt{2 z-y z} &=\sqrt{2} \
\sqrt{2 z-z x}+\sqrt{2 x-z x} &=\sqrt{3}
\end{aligned}
$$
Then $[(1-x)(1-y)(1-z)]^2$ can be written as $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.
Solution

数学竞赛代考
数学竞赛代考|AIME代考美国数学邀请赛|2022 AIME I PROBLEMS
问题1
二次多项式$P(x)$和$Q(x)$的前导系数分别为2和$2$。两个多项式的图形都经过$(16,54)$和$(20,53)$两点。求$P(0)+Q(0)$。
解答
问题2
求三位数的正整数 $underline{a}b$ \元,其基数为$underline{b}和$underline{c}。`underline{c}} a_{text {nine }}$,其中$a, b$和$c$是(不一定不同的)数字。
解决方案
问题3
在等腰梯形$A B C D$中,平行基$overline{A B}$和$overline{C D}$的长度分别为500和650,且$A D=B C=333$。A$和D$的角平分线在$P$处相遇,B$和C$的角平分线在$Q$处相遇。求$P Q$。
解答
问题4
设$w=frac{-1+i\sqrt{3}{2}$,$z=frac{-1+i\sqrt{3}{2}$,其中$i=\sqrt{-1}$。求满足方程$i\cdot w^r=z^s$的不超过100的正整数的有序对$(r, s)$的数量。
解决方法
问题5
一条宽264米的直河以每分钟14米的速度自西向东流去。梅兰妮和雪莉坐在河的南岸,梅兰妮距离雪莉的下游有$D$米。相对于水面,梅兰妮以每分钟80米的速度游泳,而雪莉以每分钟60米的速度游泳。同时,梅兰妮和雪莉开始以直线方式游向河北岸的一个点,该点与她们的起始位置等距离。两位女士同时到达该点。求$D$。
解答
问题6
求整数$(a,b)$的有序对的数目,以便使序列
$$
3,4,5, a, b, 30,40,50
$$
是严格增加的,并且没有一组四项(不一定是连续的)形成算术级数。
解决方法
问题7
设$a, b, c, d, e, f, g, h, i$为1-9的不同整数。的最小可能正值是
$$
\frac{a \cdot b \cdot c-d \cdot e \cdot f}{g \cdot h \cdot i}。
$$
可以写成$frac{m}{n}$,其中$m$和$n$是相对质的正整数。求$m+n$。
解答
问题8
等边三角形$A B C$被刻在半径为18的圆$omega$内。圆$omega_A$与边$overline{A B}$和$overline{A C}$相切,并且与$omega$相内切。圆$omega_B$和$omega_C$的定义是类似的。圆$omega_A、$omega_B$和$omega_C$在六个点上相遇–每对圆有两个点。最接近$$三角形A B C$顶点的三个交点是$$三角形A B C$内部一个大的等边三角形的顶点,另外三个交点是$$三角形A B C$内部一个小的等边三角形的顶点。较小的等边三角形的边长可以写成$/sqrt{a}-sqrt{b}$,其中$a$和$b$是正整数。求$a+b$。
解答
问题9
Ellina有12个图块,红色$(\mathbf{R})$、蓝色$(\mathbf{B})$、黄色$(\mathbf{Y})$、绿色$(\mathbf{G})$、橙色$(\mathbf{O})$、紫色$(\mathbf{P})$各两个。如果每对相同颜色的图块之间有偶数个图块,则称该图块的排列为偶数。例如,这种排列方式
r b b y g g y r oppo
是偶数。艾丽娜将她的积木按随机顺序排列成一排。她的排列是偶数的概率是$frac{m}{n}$,其中$m$和$n$是相对质的正整数。求$m+n$。
解答
问题10
三个半径分别为11,13和19的球体相互外切。一个平面与球体相交于三个全等的圆,分别以$A$、$B$和$C$为中心,球体的中心都在这个平面的同一侧。假设$A B^2=560$。求$A C^2$。
解答
问题11
设$A B C D$是一个平行四边形,$B A D<90^{circ}$。与边$overline{D A}、$overline{A B}$和$overline{B C}$相切的圆与对角线$overline{A C}$相交于$P$和$Q$,$A P<A Q$,如图。假设$A P=3,P Q=9$,而$Q C=16$。那么$A B C D$的面积可以用$m\sqrt{n}$的形式表示,其中$m$和$n$都是正整数,$n$不能被任何素数的平方整除。找到$m+n$。
问题12
对于任何有限集$X$,让$|X|$表示$X$中的元素数。定义
$$
S_n=sum|A \cap B|。
$$
其中总和取自所有的有序对$(A, B)$,使得$A$和$B$是${1,2,3, \ldots, n}$的子集,并且$|A|=|B|$。例如,$S_2=4$,因为和是在子集对上取得的
$$
(A, B) \in{(\emptyset, \emptyset), ({1},{1}), ({1},{2}), ({2},{2}), ({1,2},{1,2}) }。
$$
得到$S_2=0+1+0+1+2=4$。让$frac{S_{2022}}{S_{2021}}=frac{p}{q}$,其中$p$和$q$是相对素数的正整数。求$p+q$除以1000时的余数。
解答
问题13
设$S$是所有可以用$0形式表示的重复小数的有理数的集合。\元,其中至少有一个数字$a, b, c$或$d$为非零。让$N$作为$S$中的数字被写成最低项的分数时得到的不同分子的数量。例如,4和410都属于$S$中数字的不同分子,因为$0. \覆盖线{3636}=frac{4}{11}$和$0 . \overline{1230}=\frac{410}{3333}$. 求$N$除以1000时的余数。
解决方法
问题14
给定$三角形A B C$和它的一条边上的一个点$P$,如果$ell$穿过$P$并将$三角形A B C$分成两个周长相等的多边形,则称直线$ell$为通过$P$的三角形A B C$的分割线。设$三角形A B C$是一个三角形,其中$B C=219$,$A B$和$A C$为正整数。设$M$和$N$分别为$overline{A B}$和$overline{A C}$的中点,并假设$三角形A B C$的分割线通过$M$和$N$相交于30^{circ}$。求$三角形A B C$的周长。
解答
问题15
设$x, y$, 和$z$为正实数,满足方程组。
$$
\begin{aligned}
\sqrt{2 x-x y}+\sqrt{2 y-x y} &=1\
`sqrt{2 y-y z}+sqrt{2 z-y z} &=sqrt{2}。\ \sqrt{2 z-z x}+`sqrt{2 x-z x} &=sqrt{3}。
\end{aligned}
$$
那么$[(1-x)(1-y)(1-z)]^2$可以写成$frac{m}{n}$,其中$m$和$n$是相对质的正整数。求$m+n$。
解决方法

数学代写|离散数学代写Discrete Mathematics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
微观经济学代写
微观经济学是主流经济学的一个分支,研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富,各种图论代写Graph Theory相关的作业也就用不着 说。
线性代数代写
线性代数是数学的一个分支,涉及线性方程,如:线性图,如:以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。
博弈论代写
现代博弈论始于约翰-冯-诺伊曼(John von Neumann)提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理,这成为博弈论和数学经济学的标准方法。在他的论文之后,1944年,他与奥斯卡-莫根斯特恩(Oskar Morgenstern)共同撰写了《游戏和经济行为理论》一书,该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论,使数理统计学家和经济学家能够处理不确定性下的决策。
微积分代写
微积分,最初被称为无穷小微积分或 “无穷小的微积分”,是对连续变化的数学研究,就像几何学是对形状的研究,而代数是对算术运算的概括研究一样。
它有两个主要分支,微分和积分;微分涉及瞬时变化率和曲线的斜率,而积分涉及数量的累积,以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系,它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。
计量经济学代写
什么是计量经济学?
计量经济学是统计学和数学模型的定量应用,使用数据来发展理论或测试经济学中的现有假设,并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验,然后将结果与被测试的理论进行比较和对比。
根据你是对测试现有理论感兴趣,还是对利用现有数据在这些观察的基础上提出新的假设感兴趣,计量经济学可以细分为两大类:理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。