物理代写|PHYS4040 Quantum field theory

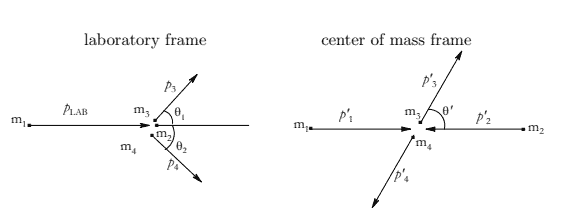
The conservation of four-momentum implies that in particle one’s rest frame,
$$
p_1^0=m_1=E_2+E_3 .
$$
By the invariance of $p_1^2, p_2^2$, and $p_3^2$, it is clear that,
$$
\begin{aligned}
p_1^2=m_1^2 & =\left(p_2+p_3\right)^2, \
& =p_2^2+p_3^2+2 p_2 p_3, \
& =m 2^2+m_3^2+2 E_2 E_3-\vec{p}_2 \overrightarrow{p_3} .
\end{aligned}
$$
But in particle one’s rest frame, $\vec{p}_2=-\vec{p}_3$ and by (1.1), $E_3=m_1-E_2$. Therefore,
$$
\begin{gathered}
m_1^2=m_2^2+m_3^2+2 m_1 E_2-2\left(E_2^2-\vec{p}_2^2\right), \
=m_3^2-m_2^2+2 m_1 E_2, \
\therefore E_2=\frac{m_1}{2}+\frac{m_2^2-m_3^2}{2 m_1} .
\end{gathered}
$$

In the center of mass frame of reference, the total 4-momentum can be described by,
$$
p_{c m}=p_1^{\prime}+p_2^{\prime}=\left(E_1+E_2 ; \overrightarrow{0}\right) \equiv\left(E_{c m} ; \overrightarrow{0}\right)
$$
Note that $p_1 p_2$ is an invariant scalar product. Evaluated in the laboratory frame,
$$
p_1 p_2=E_L m_2-\vec{p}L \overrightarrow{0}=E_L m_2 $$ This allows us to conclude that, $$ \begin{aligned} p{c m}^2 & =E_{c m}^2=p_1^{\prime 2}+p_2^{\prime 2}+2 p_1 p_2, \
\therefore E_{c m}^2 & =m_1^2+m_2^2+2 E_L m_2 .
\end{aligned}
$$
Consider the four-vectors $\eta$ and $\lambda$ defined by,
$$
\begin{array}{rr}
\eta \equiv\left(p_1+p_2\right)=\left(E_L+m_2 ; \vec{p}L\right) & \eta^{\prime} \equiv\left(E_1^{\prime}+E_2^{\prime} ; \overrightarrow{0}\right)=\left(E{c m} ; \overrightarrow{0}\right) \
\lambda \equiv\left(p_1-p_2\right)=\left(E_L-m_2 ; \vec{p}L\right) & \lambda^{\prime} \equiv\left(E_1^{\prime}-E_2^{\prime} ; 2 \vec{p}^{\prime}\right) . \end{array} $$ By the frame-invariance of the scalar product, $$ \eta \lambda=\eta^{\prime} \lambda^{\prime}=E_L^2-m_1^2-\left|\vec{p}_L\right|^2=E{c m}\left(E_1^{\prime}-E_2^{\prime}\right)
$$

Consider two concentric coplanar circles ( $r=$ constant) in Schwarzschild geometry. Suppose that the measured circumferences of these circles are $C_1$ and $C_2$. (a) What is the radial co-ordinate difference $\Delta r$ between these circles? (b) What is the measured radial distance between these two circles? (c) For the sun, take the two circles as having circumferences $C_1=2 \pi R_{\odot}$ and $C_2=4 \pi R_{\odot}$. By how many centimeters does the measured radial distance between them differ from the result expected in flat space?

Now consider the identity $\eta^{\prime 2} \lambda^{\prime 2}=\eta^2 \lambda^2$. Calculating these products and using the result above,
$$
\begin{aligned}
\eta^{\prime 2} \lambda^{\prime 2}=E_{c m}^2\left(\left(E_1^{\prime}-E_2^{\prime}\right)^2-4\left|\vec{p}1^{\prime}\right|^2\right) & =\left(\left(E_L+m_2\right)^2-\left|\vec{p}_L\right|^2\right)\left(\left(E_L-m_2\right)^2-\left|\vec{p}_L\right|^2\right)=\eta^2 \lambda^2, \ E{c m}^2\left(E_1^{\prime}-E_2^{\prime}\right)^2-4\left|\vec{p}1\right|^2 E{c m}^2 & =\left(E_L^2-m_2^2-\left|\vec{p}L\right|^2\right)^2-4 m_2^2\left|\vec{p}_L\right|^2, \ & =E{c m}^2\left(E_1^{\prime}-E_2^{\prime}\right)^2-4 m_2^2\left|\vec{p}L\right|^2, \ \therefore\left|\vec{p}_1^{\prime}\right|^2=\frac{m_2^2\left|\vec{p}_L\right|^2}{E{c m}^2} & \Rightarrow\left|\vec{p}1\right|=\frac{m_2\left|\vec{p}_L\right|}{E{c m}} .
\end{aligned}
$$
(d) By the conservation of four-momentum, $q=p_1-p_3=p_4-p_2$. So,
$$
\begin{aligned}
q^2=\left(p_4-p_2\right)^2 & =2 m_4^2-2 p_2 p_4 \
& =2 m_4^2-2 E_4 m_4 \
\therefore q^2 & =-2 m_4\left(E_4-m_4\right) .
\end{aligned}
$$

The first part of this problem, namely that $s \equiv\left(p_1+p_2\right)^2=E_{c m}^2$, was demonstrated and used in part (b) above. Let us now consider $t \equiv q^2$,
$$
t \equiv q^2=p_1^2+p_3^2-2 p_1 p_3=2 m_1^2-2 E_1^{\prime} E_3^{\prime}+2\left|\vec{p}_1^{\prime}\right|\left|\vec{p}_3^{\prime}\right| \cos \left(\theta^{\prime}\right)
$$
Here, we wrote $p_1 p_2$ explicitly in the center of mass frame. Because it is an invariant, any frame will do. Now we can use the fact that $m_1=m_3$ and $m_2=m_4$ to see that $\left|\vec{p}_1^{\prime}\right|=\left|\vec{p}_3^{\prime}\right|$ and that $E_1^{\prime}=E_3^{\prime}$ by using part (c) from above. We will now use the notation of the assignment where $\left|\vec{p}_1^{\prime}\right|=p^{\prime}$. This quickly reduces the above equality to
$$
q^2=2\left(m_1^2-E_1^{\prime 2}+p^2 \cos \left(\theta^{\prime}\right)\right) \text {. }
$$
This can be simplified in two ways. First, notice that $m_1^2-E_1^{\prime 2}=-p^{\prime 2}$ because $E_1^{\prime 2}-p^{\prime 2}=$ $m_1^2$. Second we will use the trigonometric identity $1-\cos (\alpha)=2 \sin ^2(\alpha / 2)$. Introducing these simplifications we obtain
$$
q^2=-4 p^2 \sin ^2\left(\theta^{\prime} / 2\right) .
$$