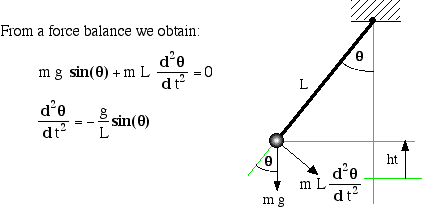数学代写|Math220 Ordinary Differential Equations

(1) Solve
$$
y u_x+x u_y=0, u(0, y)=e^{-y^2}
$$
(2) In which region is u uniquely determined?
Solution. This is a homogeneous linear PDE with no first order term, so its solutions are functions which are constant along the projected characteristic curves, i.e. the integral curves of the vector field $V(x, y)=(y, x)$. Note also that the initial curve, the $y$-axis, is characteristic at exactly one point, namely the origin, where $V$ vanishes. Elsewhere along the $y$ axis $V(0, y)=(y, 0)$ which is not tangent to the $y$-axis.
The characteristic equations in this case are
$$
\frac{d x}{d s}=y, \frac{d y}{d s}=x, \frac{d z}{d s}=0 .
$$
The $z$ ODE is trivial: $z=c_3(r)$. One can find the solution of the $(x, y)$ ODEs either by obtaining a second order ODE for $x$ :
$$
\frac{d^2 x}{d s^2}=\frac{d y}{d s}=x
$$
whose solutions are $x=c_1(r) e^s+c_2(r) e^{-s}$. As $y=\frac{d x}{d s}$, this gives
$$
(x, y, z)=\left(c_1(r) e^s+c_2(r) e^{-s}, c_1(r) e^s-c_2(r) e^{-s}, c_3(r)\right)
$$

Thus, $x+y=2 c_1(r) e^s, x-y=2 c_2(r) e^{-s}$, so $x^2-y^2=(x+y)(x-y)=4 c_1(r) c_2(r)$, i.e. is a constant along the projected characteristic curves. In other words, the projected characteristic curves are $x^2-y^2=C, C$ a constant, and the solution is a function that is constant along these. One has to be slightly careful, as the same value of $C$ corresponds to two characteristic curves, see the argument two paragraphs below concerning the sign of $r$. In particular, any function $f$ of $x^2-y^2$ will solve the PDE. As we want $f\left(x^2-y^2\right)=u(x, y)$ to satisfy $u(0, y)=e^{-y^2}$, we deduce that $f\left(-y^2\right)=e^{-y^2}$ for all real $y$, i.e. $f(t)=e^t$ for $t \leq 0$. Note that $f(t)$ is not defined by this restriction for $t>0$. So one obtains that $u(x, y)=f\left(x^2-y^2\right)$ solves the PDE where $f(t)=e^t$ for $t \leq 0, f(t)$ arbitrary for $t>0$.

In particular, the solution is not unique where $x^2-y^2>0$, i.e. where $|x|>|y|$. This is exactly the region in which the characteristic curves do not approach the $y$ axis.

To see how our usual method of substituting in the initial conditions works, note that the initial data curve is $\left(0, r, e^{-r^2}\right)$, so at $s=0$ we get $c_1(r)+c_2(r)=0$, $c_1(r)-c_2(r)=r, c_3(r)=e^{-r^2}$, so the solution of the characteristic ODEs taking into account the initial conditions is
$$
(x, y, z)=\left(\frac{r}{2}\left(e^s-e^{-s}\right), \frac{r}{2}\left(e^s+e^{-s}\right), e^{-r^2}\right)=\left(r \sinh s, r \cosh s, e^{-r^2}\right) .
$$

As $\cosh ^2 s-\sinh ^2 s=1$, we deduce that $y^2-x^2=r^2$ along the projected characteristic curves. This gives that $|y| \geq|x|$ in the region where the projected characteristic curves crossing the $y$ axis reach. In this region, $r= \pm \sqrt{y^2-x^2}$, with the the sign \pm agreeing with the sign of $y$ (i.e. is + where $y>0$ ). In any case, the solution is $u(x, y)=e^{-r^2}=e^{x^2-y^2}$ in $|y| \geq|x|$. Note that this method does not give the solution in the region $|y|<|x|$, as the projected characteristic curves never reach the region. Note also that there is no neighborhood of the origin in which this method gives $u$; this is because the $y$-axis is characteristic for this PDE at the origin.

A simpler way of finding the projected characteristic curves is to parameterize them by $x$ or $y$. In the former case, one gets
$$
\frac{d y}{d x}=\frac{\frac{d y}{d s}}{\frac{d x}{d s}}=\frac{x}{y},
$$
so $\int y d y=\int x d x$, i.e. $y^2=x^2+C$. Again, $C$ is a parameter.

(1) Solve $u_x+u_t=u^2, u(x, 0)=e^{-x^2}$.
(2) Show that there is $T>0$ such that $u$ blows up at time T, i.e. $u$ is continuously differentiable for $t \in[0, T), x$ arbitrary, but for some $x_0,\left|u\left(x_0, t\right)\right| \rightarrow$ $\infty$ as $t \rightarrow T-$. What is $T$ ?
Solution. The characteristic ODEs are
$$
\frac{d x}{d s}=1, \frac{d t}{d s}=1, \frac{d z}{d s}=z^2
$$
The solution is
$$
\begin{aligned}
& x(r, s)=s+c_1(r), \
& t(r, s)=s+c_2(r), \
& -z^{-1}=s+c_3(r) \Rightarrow z=\frac{-1}{s+c_3(r)} .
\end{aligned}
$$
The initial conditions give that at $s=0,(x, t, z)=\left(r, 0, e^{-r^2}\right)$, so $c_1(r)=r$, $c_2(r)=0, c_3(r)=-e^{r^2}$. Thus
$$
(x, t, z)=\left(s+r, s, \frac{-1}{s-e^{r^2}}\right) .
$$
Inverting the map $(r, s) \mapsto(x(r, s), t(r, s))$ yields $s=t, r=x-s=x-t$, so
$$
u(x, t)=z(r(x, t), s(x, t))=\frac{-1}{t-e^{(x-t)^2}} .
$$
Note that the denominator vanishes only if $t=e^{(x-t)^2}$, and $(x-t)^2 \geq 0$, so the denominator can only vanish if $t \geq 1$. In particular, $u$ is a $C^1$, indeed $C^{\infty}$, function on $\mathbb{R}_x \times[0,1)_t$. On the other hand, for $x=1$, as $t \rightarrow 1-, u(x, t)=\frac{-1}{t-e^{(1-t)^2}} \rightarrow+\infty$, i.e. the solution blows up at $T=1$ (at $\left.x_0=1\right)$.

Solve
$$
u_t+u u_x=0, u(x, 0)=-x^2
$$
for $|t|$ small.
Solution. We parameterize the $x$-axis as $\Gamma(r)=(r, 0)$, and note that the vector field $(z, 1)$ is not tangent to $\Gamma$ at any point regardless of the value of $z$, so this is a non-characteristic initial value problem. The characteristic equations are
$$
\begin{aligned}
& \frac{\partial t}{\partial s}=1, t(r, 0)=0 \
& \frac{\partial x}{\partial s}=z, x(r, 0)=r \
& \frac{\partial z}{\partial s}=0, z(r, 0)=-r^2
\end{aligned}
$$

The solution is
$$
\begin{aligned}
& t(r, s)=s, \
& z(r, s)=-r^2, \
& x(r, s)=-r^2 s+r .
\end{aligned}
$$
Thus, $s=t$, and $t r^2-r+x=0$, so if $t=0$ then $r=x$, and if $t \neq 0$ then $r$ solves
$$
r=\frac{1 \pm \sqrt{1-4 t x}}{2 t}
$$
The choice of the sign is dictated by $r=x$ when $t=0$ (i.e. by taking the limit as $t \rightarrow 0$ using, say, L’Hospital’s rule), so one needs the negative sign, and
$$
r=\frac{1-\sqrt{1-4 t x}}{2 t}
$$
The solution is then
$$
u(x, t)=-R(x, t)^2=-\frac{(1-\sqrt{1-4 t x})^2}{4 t^2}, t \neq 0,
$$
and $u(x, 0)=-x^2$.