MY-ASSIGNMENTEXPERT™可以为您提供math Math46400 Number theory 数论的代写代考和辅导服务!
这是纽约市立学院数论课程的代写成功案例。
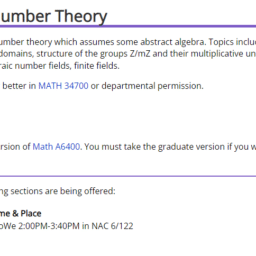
Math46400简介
A first course in algebraic number theory which assumes some abstract algebra. Topics include: unique factorization in the integers and Euclidean domains, structure of the groups Z/mZ and their multiplicative units, quadratic residues and quadratic reciprocity, algebraic number fields, finite fields.
Prerequisites: Grade of C or better in MATH 34700 or departmental permission.
Contact Hours: 4 hr./wk.
Credits: 4
This is an undergraduate version of Math A6400. You must take the graduate version if you want graduate credit.
Prerequisites
Number theory or arithmetic or higher arithmetic in older usage is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. German mathematician Carl Friedrich Gauss (1777–1855) said, “Mathematics is the queen of the sciences—and number theory is the queen of mathematics.”
Math46400 Number theory HELP(EXAM HELP, ONLINE TUTOR)
In Divisibility Exercise 2 at the end of Section 5 in our book, we conjectured for which $n$-values $2^n+1$ is divisible by 3 . Now we prove our conjecture. That is, prove the following:
For all positive odd integers $n$, we have 3 divides $2^n+1$.
NOTE: As stated in the footnote of Divisibility Exercise 2, there exists a slick way to do this proof using congruence theory which we have not covered yet. You are NOT permitted to use this method for this problem-even if we covered congruence theory by now.
HINT: Consider inducting on odd positive values $n$, or ANY method you feel comfortable with EXCEPT congruence theory!
Prove that if $m \mid x$ and $n \mid x$ and $\operatorname{gcd}(m, n)=1$, then $m n \mid x$.
HINT: You may find it very useful to use Bézout’s Identity (Theorem 5.20 in our coursebook).
Let $m_1, m_2, \ldots, m_r \in \mathbb{N}$ and set $n=\operatorname{lcm}\left(m_1, m_2, \ldots, m_r\right)$. Prove that for $t \in \mathbb{Z}$, we have
$$
m_i \mid t \text { for all } i=1,2, \ldots, r \Longleftrightarrow n \mid t \text {. }
$$
NOTE: This result will be used in a proof of Theorem 6.9 in the congruence theory section.
These are warm up problems that do not need to be turned in.
(a) In class we gave an elementary proof that $\vartheta(x)=O(x)$. Give a similarly elementary proof that $x=O(\vartheta(x))$ (both bounds were proved by Chebyshev before the PNT).
(b) Prove the Möbius inversion formula, which states that if $f$ and $g$ are functions $\mathbb{Z}{\geq 1} \rightarrow \mathbb{C}$ that satisfy $g(n)=\sum{d \mid n} f(d)$ then $f(n)=\sum_{d \mid n} \mu(d) g(n / d)$, where $\mu(n):=(-1)^{#{p \mid n}}$ if $n$ is squarefree and $\mu(n)=0$ otherwise.
(c) Verify that for all Schwartz functions $f, g \in \mathcal{S}(\mathbb{R})$ we have
$$
\widehat{f * g}=\hat{f} \hat{g}, \quad \text { and } \quad \widehat{f g}=\hat{f} * \hat{g}
$$
(the Fourier transform turns convolutions into products and vice versa).
Let $Z(s):=\pi^{-s / 2} \Gamma\left(\frac{s}{2}\right) \zeta(s)$ denote the completed zeta function; we proved in class that it has the integral representation
$$
Z(s)=\int_1^{\infty} \sum_{n=1}^{\infty} e^{-\pi n^2 x}\left(x^{s / 2}+x^{(1-s) / 2}\right) \frac{d x}{x}-\frac{1}{s}-\frac{1}{1-s},
$$
and extends to a meromorphic function on $\mathbb{C}$ with functional equation $Z(s)=Z(1-s)$.
Recall Hadamard’s Factorization Theorem: if $f(s)$ is an entire function and $n$ is an integer for which there exists a positive $c<n+1$ such that $|f(s)|=O\left(\exp \left(|s|^c\right)\right)$ then
$$
f(s)=s^m e^{g(s)} \prod_\rho\left(1-\frac{s}{\rho}\right) E_n\left(\frac{s}{\rho}\right),
$$
where $m=\operatorname{ord}0(f), g \in \mathbb{C}[s]$ has degree at most $n$, the product ranges overs zeros $\rho \neq 0$ of $f(s)$ (with multiplicity), and $E_n(z)=\exp \left(\sum{k=1}^n \frac{z^k}{k}\right)$.
(a) Prove that we can apply (1) to $f(s):=s(s-1) Z(s)$ with $n=1$ and $m=0$.
(b) Prove that we can apply (1) to $f(s):=\Gamma(s)^{-1}$ with $n=1$ and $m=1$.
(c) Prove that
$$
(s-1) \zeta(s)=e^{a+b s} \prod_\rho\left(1-\frac{s}{\rho}\right) e^{\frac{s}{\rho}} \prod_{n=1}^{\infty}\left(1+\frac{s}{2 n}\right) e^{-\frac{s}{2 n}}
$$
for some $a, b \in \mathbb{C}$, where $\rho$ ranges over the zeros of $\zeta(s)$ in the critical strip.
(d) Using (c) and the Euler product for $\zeta(s)$, show that $b=\frac{\zeta^{\prime}(0)}{\zeta(0)}-1$ and
$$
\begin{aligned}
& \qquad \sum_p \sum_{m \geq 1} p^{-m s} \log p=\frac{s}{s-1}-\frac{\zeta^{\prime}(0)}{\zeta(0)}-\sum_\rho\left(\frac{1}{s-\rho}+\frac{1}{\rho}\right)-\sum_{n \geq 1}\left(\frac{1}{s+2 n}-\frac{1}{2 n}\right) \
& \text { on } \operatorname{Re}(s)>1 \text {. }
\end{aligned}
$$
We now recall the identity
$$
\frac{1}{2 \pi i} \int_{\sigma-i \infty}^{\sigma+i \infty} \frac{x^s}{s} d s= \begin{cases}1 & \text { if } x>1 \ 0 & \text { if } 00$, and define the Perron integral transform
$$
f \mapsto \lim {t \rightarrow \infty} \frac{1}{2 \pi i} \int{\sigma-i t}^{\sigma+i t} f(s) \cdot \frac{x^s}{s} d s
$$
valid for any $x, \sigma>0$, and define the Perron integral transform
$$
f \mapsto \lim {t \rightarrow \infty} \frac{1}{2 \pi i} \int{\sigma-i t}^{\sigma+i t} f(s) \cdot \frac{x^s}{s} d s
$$
We also define an alternative version of Chebyshev’s function
$$
\psi(x):=\sum_{p^n \leq x} \log p
$$
where the sum is over all prime powers $p^n \leq x$ (but note that we take $\log p$ not $\log p^n$ ).
(e) Fix $x>1$ not a prime power. By applying the Perron integral transform to both sides of the equation in (d), and assuming that the RHS can be computed by applying Cauchy’s residue formula term by term to the sums (and that the Perron integral transform converges in each case), deduce the explicit formula
$$
\psi(x)=x-\sum_\rho \frac{x^\rho}{\rho}-\frac{\zeta^{\prime}(0)}{\zeta(0)}+\sum_n \frac{x^{-2 n}}{2 n},
$$
where $\rho$ ranges over the the non-trivial zeros of $\zeta(s)$.
(f) Fix $c \in[1 / 2,1)$ and suppose that $\zeta(s)$ has no zeros in the strip $c<\operatorname{Re}(s)<1$. Assume that the number of zeros $\rho$ with $|\operatorname{Im}(\rho)| \leq T$ is bounded by $O(T \log T)$. Derive the following bounds: $\psi(x)=x+O\left(x^{c+\epsilon}\right), \vartheta(x)=x+O\left(x^{c+\epsilon}\right)$, and $\pi(x)=$ $\operatorname{Li}(x)+O\left(x^{c+\epsilon}\right)$, for any $\epsilon>0$ (in fact one replace $\epsilon$ with $\left.o(1)\right)$.

MY-ASSIGNMENTEXPERT™可以为您提供MATH MATH46400 NUMBER THEORY 数论的代写代考和辅导服务!