MY-ASSIGNMENTEXPERT™可以为您提供Stanford EE261 Fourier analysis傅里叶分析的代写代考和辅导服务!
这是斯坦福大学 傅里叶分析课程的代写成功案例。
EE261课程简介
The goals for the course are to gain a facility with using the Fourier transform, both specific techniques and general principles, and learning to recognize when, why, and how it is used. Together with a great variety, the subject also has a great coherence, and the hope is students come to appreciate both.
Topics include: The Fourier transform as a tool for solving physical problems. Fourier series, the Fourier transform of continuous and discrete signals and its properties. The Dirac delta, distributions, and generalized transforms. Convolutions and correlations and applications; probability distributions, sampling theory, filters, and analysis of linear systems. The discrete Fourier transform and the FFT algorithm. Multidimensional Fourier transform and use in imaging. Further applications to optics, crystallography. Emphasis is on relating the theoretical principles to solving practical engineering and science problems.
Prerequisites
e goals for the course are to gain a facility with using the Fourier transform, both specific techniques and general principles, and learning to recognize when, why, and how it is used. Together with a great variety, the subject also has a great coherence, and the hope is students come to appreciate both.
Topics include:
- The Fourier transform as a tool for solving physical problems.
- Fourier series, the Fourier transform of continuous and discrete signals and its properties.
- The Dirac delta, distributions, and generalized transforms.
- Convolutions and correlations and applications; probability distributions, sampling theory, filters, and analysis of linear systems.
- The discrete Fourier transform and the FFT algorithm.
- Multidimensional Fourier transform and use in imaging.
- Further applications to optics, crystallography.
- Emphasis is on relating the theoretical principles to solving practical engineering and science problems.
EE261 Fourier analysis HELP(EXAM HELP, ONLINE TUTOR)
Compute the Fourier transform of the characteristic function of the interval $[-a, a]$, where $a>0$.
Solution. For any $\xi \in \mathbb{R} \backslash{0}$, we have
$$
\begin{aligned}
\widehat{\chi_{[-a, a]}}(\xi) & =\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \chi_{[-a, a]}(x) e^{-i x \xi} \mathrm{d} x \
& =\frac{1}{\sqrt{2 \pi}} \int_{-a}^a e^{-i x \xi} \mathrm{d} x=\frac{e^{-i a \xi}-e^{i a \xi}}{-\sqrt{2 \pi} i \xi}=\sqrt{\frac{2}{\pi}} \cdot \frac{\sin a \xi}{\xi} .
\end{aligned}
$$
Since $\chi_{[-a, a]} \in \mathscr{L}^1(\mathbb{R})$, the Fourier transform $\widehat{\chi_{[-a, a]}}$ is continuous and we must have
$$
\widehat{\chi_{[-a, a]}}(0)=\lim {\xi \rightarrow 0} \widehat{\chi{[-a, a]}}(\xi)=\lim _{\xi \rightarrow 0} \sqrt{\frac{2}{\pi}} \cdot \frac{\sin a \xi}{\xi}=\sqrt{\frac{2}{\pi}} \cdot a
$$
Compute the Fourier transform of the function
$$
f(x)= \begin{cases}1-|x|, & |x| \leqslant 1 \ 0, & |x|>1\end{cases}
$$
Solution. Again we may compute the Fourier transform directly for any $\xi \in \mathbb{R} \backslash{0}$
$$
\begin{aligned}
\widehat{f}(\xi) & =\frac{1}{\sqrt{2 \pi}} \int_{-1}^1(1-|x|) e^{-i x \xi} \mathrm{d} x=\sqrt{\frac{2}{\pi}} \int_0^1(1-x) \cos x \xi \mathrm{d} x \
& \left.\left.=\sqrt{\frac{2}{\pi}}\left(\frac{\sin x \xi}{\xi}\right]0^{x=1}-\frac{x \sin x \xi}{\xi}\right]_0^{x=1}+\frac{1}{\xi} \int_0^1 \sin x \xi \mathrm{d} \xi\right) \ & \left.=\sqrt{\frac{2}{\pi}}\left(\frac{\sin \xi}{\xi}-\frac{\sin \xi}{\xi}-\frac{\cos x \xi}{\xi^2}\right]_0^{x=1}\right) \ & =\sqrt{\frac{2}{\pi}} \cdot \frac{-\cos \xi+1}{\xi^2}=\sqrt{\frac{2}{\pi}} \cdot \frac{2 \sin ^2 \frac{\xi}{2}}{\xi^2} \end{aligned} $$ Since clearly $f \in \mathscr{L}^1(\mathbb{R})$, we obtain $\widehat{f}(0)$ as in the previous exercise: $$ \widehat{f}(0)=\lim {\xi \rightarrow 0} \sqrt{\frac{2}{\pi}} \cdot \frac{2 \sin ^2 \frac{\xi}{2}}{\xi^2}=\sqrt{\frac{2}{\pi}} \cdot 2 \cdot\left(\frac{1}{2}\right)^2=\frac{1}{\sqrt{2 \pi}} .
$$
(a) Find the Fourier series:
$$
a_0+\sum_{k=1}^{\infty}\left(a_k \cos (k x)+b_k \sin (k x)\right)
$$
for the function:
$$
f(x)=\left{\begin{array}{llr}
\pi-x & \text { if } \quad 0 \leq x<\pi \
x+\pi & \text { if } \quad-\pi \leq x<0
\end{array}\right.
$$
(extended periodically over the real line)
(b) Graph the finite trigonometric sums for $N=2,5,20$. (Use Python or some other graphing utility.)
(a) Find the Fourier series for the function:
$$
f(x)=\left{\begin{array}{lrr}
x & \text { if } & 0 \leq x<\pi \
0 & \text { if } & -\pi \leq x<0
\end{array}\right.
$$
(extended periodically over the real line)
$$
\begin{aligned}
a_0 & =\frac{1}{2 \pi} \int_{-\pi}^\pi f(x) d x \
& =\frac{1}{2 \pi} \int_0^\pi x d x \
& =\left.\frac{1}{2 \pi} \frac{x^2}{2}\right|0 ^\pi \ & =\frac{1}{2 \pi}\left[\frac{\pi^2}{2}-\frac{0^2}{2}\right] \ & =\frac{\pi}{4} \ a_n & =\frac{1}{\pi} \int{-\pi}^\pi f(x) \cos (n x) d x \
& =\frac{1}{\pi} \int_0^\pi x \cos (n x) d x \
& =\frac{1}{\pi}\left[\left.\frac{x \sin (n x)}{n}\right|_0 ^\pi-\int_0^\pi \frac{\sin (n x)}{n} d x\right] \
& =\frac{1}{\pi}\left[0-0+\frac{\cos (n x)}{n^2}\right]_0^\pi \
& =\frac{1}{\pi n^2}(\cos (n \pi)-\cos (0)) \
& =\frac{(-1)^n-1}{\pi n^2}
\end{aligned}
$$
$$
a_n= \begin{cases}0 & \text { if } n=2 k \ \frac{-2}{\pi(2 k-1)^2} & \text { if } n=2 k-1\end{cases}
$$
Finally,
$$
\begin{aligned}
b_n & =\frac{1}{\pi} \int_{-\pi}^\pi f(x) \sin (n x) d x \
& =\frac{1}{\pi} \int_0^\pi x \sin (n x) d x \
& =\frac{1}{\pi}\left[-\left.\frac{x \cos (n x)}{n}\right|0 ^\pi-\int_0^\pi \frac{-\cos (n x)}{n} d x\right] \ & =\frac{1}{\pi}\left[-\frac{\pi \cos (n \pi)}{n}-0+\frac{\sin (n x)}{n^2}\right]_0^\pi \ & =\frac{(-1)^{n+1}}{n} \end{aligned} $$ So, $$ \operatorname{trig} \text { series }=\frac{\pi}{4}-\frac{2}{\pi} \sum{k=1}^{\infty} \frac{\cos ((2 k-1) x)}{(2 k-1)^2}+\sum_{k=1}^{\infty} \frac{(-1)^{k+1} \sin (k x)}{k}
$$
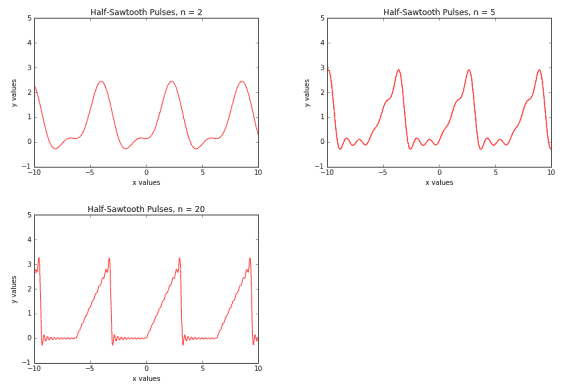
(b) Graph the finite trigonometric sums for $N=2,5,20$.

MY-ASSIGNMENTEXPERT™可以为您提供STANFORD EE261 FOURIER ANALYSIS傅里叶分析的代写代考和辅导服务!