my-assignmentexpert™ Economics 经济学作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 $100 \%$ 原创。my-assignmentexpert™, 最高质量的ECON经济学作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此经济作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济代写服务。我们的专家在经济学 代写方面经验极为丰富,各种economics相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 微观经济学
- 货币银行学
- 数量经济学
- 宏观经济学
- 经济统计学
- 经济学理论
- 商务经济学
- 计量经济学
- 金融经济学
- 国际经济学
- 健康经济学
- 劳动经济学
Econ经济作业代写Economics代考|Revisiting mixed-strategy equilibria
Continuous types|Econ经济作业代写Economics代考
Consider, now, the density distribution depicted in figure XVII.2. The density is equal to $1 / x$ for types between 0 and $x$ and 0 for other types:
$$
\tau^{x}(a)= \begin{cases}\frac{1}{x}, & a \in[0, x] \ 0, & a \notin[0, x]\end{cases}
$$
For this density distribution, we find
$$
\tau^{x}([a, b])=\int_{a}^{b} \tau^{x}(t) d t=\frac{b-a}{x}, 0 \leq a \leq b \leq x
$$
This formula implies that the probability for a specific type $a$ is zero:
$$
\tau^{x}([a, a])=\frac{a-a}{x}=0
$$
Thus, while $\tau^{x}$ is a probability distribution on $[0, x] \times[0, x]$ in the first place, it can also be understood as a probability (or density) distribution on $[0, x]$. Since we assume identical densities for players 1 and $2, \tau^{x}([a, b])$ can refer to either of them. Please distinguish $\tau^{x}([a, a])$ from $\tau^{x}(a) . \tau^{x}([a, a])$ is the
Introducing uncertainty|ECON经济作业代写ECONOMICS代考
We now construct a static Bayesian game. Cathy and Peter know their own types, $t_{C}$ and $t_{P}$, respectively, but not the other player’s type. We assume $t_{C}, t_{P} \in[0, x]$ for some number $x>0$ and also a constant density $\frac{1}{x}$. Thus, we have
$$
\tau^{x}([a, b])=\frac{b-a}{x} .
$$
Formally, the corresponding static Bayesian game $\Gamma^{x}=(N, A, T, \tau, u)$ is given by
- $N={C, P}$,
- $A_{C}=A_{P}={$ theatre, football $}$,
- $T_{C}=T_{P}=[0, x]$,
- the probability distribution $\tau^{x}$ on $T_{C} \times T_{P}$ defined in the previous section, and
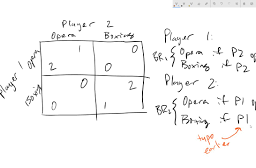
- the payoff functions $u_{C}: A_{C} \times A_{P} \times T_{C} \rightarrow \mathbb{R}$ and $u_{P}: A_{C} \times A_{P} \times$ $T_{P} \rightarrow \mathbb{R}$ defined by the above matrix.
The equilibria|Econ经济作业代写Economics代考
$$
\begin{aligned}
&L={1,2, \ldots, 100} \
&R={101, \ldots, 199}
\end{aligned}
$$
If a payoff vector
$$
\left(x_{1}, \ldots, x_{100}, x_{101}, \ldots, x_{199}\right)
$$
is to belong to the core, we have
$$
\sum_{i=1}^{199} x_{i}=99
$$
by the efficiency axiom. We now pick any left-glove holder $j \in{1,2, \ldots, 100}$. We find
$$
v(L \backslash{j} \cup R)=99
$$
- FIVE NON-SIMPLE GAMESand hence
$$
\begin{aligned}
x_{j} &=99-\sum_{\substack{i=1 \
i \neq j}}^{199} x_{i}(\text { efficiency) }\
&\leq 99-99 \text { (blockade by coalition } L \backslash{j} \cup R) \
&=0
\end{aligned}
$$
Therefore, we have $x_{j}=0$ for every $j \in L$.
Every right-glove owner can claim at least 1 because he can point to coalitions where he is joined by at least one left-glove owner. Therefore, every right-glove owner obtains the payoff 1 and every left-glove owner the payoff zero. Inspite of the fact that the scarcity is minimal, the right-glove owners get evervthing.
The chess game|Econ经济作业代写Economics代考
EXERCISE XVII.5. Find Peter’s threshold type $\bar{t}{P}$ if Cathy’s probability for choosing theatre is $\theta{C}$ !
Summarizing the results so far,
- Cathy chooses theatre if $t_{C} \geq \bar{t}{C}:=\frac{1-3 \theta{P}}{\theta_{P}}$ while
- Peter chooses theatre in case of $t_{P} \leq \bar{t}{P}:=\frac{3 \theta{C}-2}{1-\theta_{C}}$.
Of course, Peter’s probability for theatre, $\theta_{P}$, is related to his threshold type $\bar{t}{P}$. By equation XVII.2, we find $$ \theta{P}=\tau^{x}\left(\left[0, \bar{t}{P}\right]\right)=\frac{\bar{t}{P}-0}{x}
$$
Similarly, we obtain
$$
\theta_{C}=\tau^{x}\left(\left[\bar{t}{C}, x\right]\right)=\frac{x-\bar{t}{C}}{x}
$$
Using the above definitions of $\bar{t}{C}$ and $\bar{t}{P}$, we get two equations in two unknowns:
$$
\begin{gathered}
\bar{t}{C}=\frac{1-3 \theta{P}}{\theta_{P}}=\frac{1-3 \frac{\bar{t}{P}}{x}}{\frac{\bar{t}{P}-0}{x}}=\frac{x-3 \bar{t}{P}}{\bar{t}{P}} \text { and } \
\bar{t}{P}=\frac{3 \theta{C}-2}{1-\theta_{C}}=\frac{3 \frac{x-\bar{t}{C}}{x}-2}{1-\frac{x-\bar{t}{C}}{x}}=\frac{x-3 \bar{t}{C}}{\bar{t}{C}} .
\end{gathered}
$$
EXERCISE XVII.6. Confirm $\bar{t}{C}=\bar{t}{P}$ ! Hint: Consider $\bar{t}{C} \bar{t}{P}$.
We now solve the quadratic equation
$$
\vec{t}^{2}+3 \bar{t}-x=0
$$
to find
$$
\bar{t}{1,2}=-\frac{3}{2} \pm \sqrt{\frac{9}{4}+x} $$ Since the sought-after threshold types belong to $[0, x]$, we obtain $$ \bar{t}{C}^{}=\bar{t}_{P}^{}=-\frac{3}{2}+\sqrt{\frac{9}{4}+x}
$$
which specify the equilibrium for every $x>0$ :
Purification|ECON经济作业代写ECONOMICS代考
3.4. Purification. We now turn to the clou of the whole exercise. Above, we have found Cathy’s mixed-equilibrium strategy $\left(\frac{2}{3}, \frac{1}{3}\right)$. We can reproduce this strategy by considering $x=0$. For a given $x>0$, Cathy’s probability for choosing theatre is
$$
\begin{aligned}
\theta_{C} &=\frac{x-\bar{t}{C}}{x}=\frac{x-\left(-\frac{3}{2}+\sqrt{\frac{9}{4}+x}\right)}{x} \ &=1-\frac{-\frac{3}{2}+\sqrt{\frac{9}{4}+x}}{x} . \end{aligned} $$ Here, we cannot substitute $x$ for 0 because then we have $\frac{0}{0}$ which is not defined. However, we can apply de l’Hospital’s rule which is theorem VIII.1 (р. 223): $$ \begin{aligned} \lim {x \rightarrow 0}\left(1-\frac{-\frac{3}{2}+\sqrt{\frac{9}{4}+x}}{x}\right) &=\lim {x \rightarrow 0} 1-\lim {x \rightarrow 0} \frac{-\frac{3}{2}+\sqrt{\frac{9}{4}+x}}{x} \
&=1-\lim {x \rightarrow 0} \frac{\frac{1}{2 \sqrt{\frac{9}{4}+x}} \cdot 1}{1} \text { (de l’Hospital’s rule) } \ &=1-\lim {x \rightarrow 0} \frac{\frac{1}{2 \cdot \frac{3}{2}} \cdot 1}{1} \
&=\frac{2}{3}
\end{aligned}
$$
Thus, Cathy’s probabilities in the static Bayesian games (which depend on $x$ ) converge to the mixed-strategy probability in the matrix game. Since Cathy chooses a pure action (in dependence on her type), substituting a

CONTINUOUS TYPES|ECON经济作业代写ECONOMICS代考
现在考虑图 XVII.2 中描绘的密度分布。密度等于1/X对于 0 到X其他类型为 0:
τX(一种)={1X,一种∈[0,X] 0,一种∉[0,X]
对于这种密度分布,我们发现
τX([一种,b])=∫一种bτX(吨)d吨=b−一种X,0≤一种≤b≤X
这个公式意味着特定类型的概率一种为零:
τX([一种,一种])=一种−一种X=0
因此,虽然τX是一个概率分布[0,X]×[0,X]首先,它也可以理解为概率(或密度)分布[0,X]. 由于我们假设玩家 1 和2,τX([一种,b])可以参考其中任何一个。请区分τX([一种,一种])从τX(一种).τX([一种,一种])是个
INTRODUCING UNCERTAINTY|ECON经济作业代写ECONOMICS代考
我们现在构建一个静态贝叶斯博弈。凯茜和彼得知道他们自己的类型,吨C和吨磷,但不是其他玩家的类型。我们猜测吨C,吨磷∈[0,X]对于一些数字X>0还有一个恒定的密度1X. 因此,我们有
τX([一种,b])=b−一种X.
形式上,对应的静态贝叶斯博弈ΓX=(ñ,一种,吨,τ,你)是(谁)给的
- ñ=C,磷,
- 一种C=一种磷=$吨H和一种吨r和,F○○吨b一种一世一世$,
- 吨C=吨磷=[0,X],
- 概率分布τX在吨C×吨磷在上一节中定义,并且
- 支付函数你C:一种C×一种磷×吨C→R和你磷:一种C×一种磷× 吨磷→R由上述矩阵定义。
THE EQUILIBRIA|ECON经济作业代写ECONOMICS代考
一世=1,2,…,100 R=101,…,199
如果一个支付向量
(X1,…,X100,X101,…,X199)
是属于核心的,我们有
∑一世=1199X一世=99
由效率公理。我们现在选择任何左手套架j∈1,2,…,100. 我们发现
v(一世∖j∪R)=99
- 五个非简单游戏因此
Xj=99−∑一世=1 一世≠j199X一世( 效率) ≤99−99 (联军封锁 一世∖j∪R) =0
因此,我们有Xj=0对于每个j∈一世.
每个右手套拥有者至少可以声明 1,因为他可以指出至少有一名左手套拥有者加入的联盟。因此,每个右手套拥有者获得收益 1,每个左手套拥有者获得收益 0。尽管稀缺性很小,但正确的手套所有者却得到了一切。
THE CHESS GAME|ECON经济作业代写ECONOMICS代考
练习 XVII.5。求 Peter 的阈值类型 $\bar{t} {P}一世FC一种吨H和′spr○b一种b一世一世一世吨和F○rCH○○s一世nG吨H和一种吨r和一世s\theta {C}$ !
总结到目前为止的结果,
- 如果 $t_{C} \geq \bar{t} {C}:=\frac{1-3 \theta {P}}{\theta_{P}}$ 则Cathy 选择剧院
- Peter 在 $t_{P} \leq \bar{t} {P}:=\frac{3 \theta {C}-2}{1-\theta_{C}}的情况下选择剧院.○FC○你rs和,磷和吨和r′spr○b一种b一世一世一世吨和F○r吨H和一种吨r和,\水龙头},一世sr和一世一种吨和d吨○H一世s吨Hr和sH○一世d吨和p和\bar{t} {P}.乙和和q你一种吨一世○nX五一世一世.2,在和F一世nd$ \theta {P}=\tau^{x}\left(\left[0, \bar{t} {P}\right]\right)=\frac{\bar{t} {P}-0} {X}
小号一世米一世一世一种r一世和,在和○b吨一种一世n
\theta_{C}=\tau^{x}\left(\left[\bar{t} {C}, x\right]\right)=\frac{x-\bar{t} {C}}{ x}
$$
使用上述 $\bar{t} {C}的定义一种nd\bar{t} {P},在和G和吨吨在○和q你一种吨一世○ns一世n吨在○你n到n○在ns:$
\begin{聚集}
\bar{t} {C}=\frac{1-3 \theta {P}}{\theta_{P}}=\frac{1-3 \frac{\bar{t} { P}}{x}}{\frac{\bar{t} {P}-0}{x}}=\frac{x-3 \bar{t} {P}}{\bar{t} {P }} \text { 和 } \
\bar{t} {P}=\frac{3 \theta {C}-2}{1-\theta_{C}}=\frac{3 \frac{x-\bar {t} {C}}{x}-2}{1-\frac{x-\bar{t} {C}}{x}}=\frac{x-3 \bar{t} {C}} {\bar{t} {C}} 。
\end{gathered}
$$
EXERCISE XVII.6。确认 $\bar{t} {C}=\bar{t} {P}!H一世n吨:C○ns一世d和r\bar{t} {C} \bar{t} {P}.在和n○在s○一世v和吨H和q你一种dr一种吨一世C和q你一种吨一世○n吨→2+3吨¯−X=0吨○F一世nd$
\bar{t} {1,2}=-\frac{3}{2} \pm \sqrt{\frac{9}{4}+x}小号一世nC和吨H和s○你GH吨−一种F吨和r吨Hr和sH○一世d吨和p和sb和一世○nG吨○$[0,X]$,在和○b吨一种一世n\bar{t} {C}^{ }=\bar{t}_{P}^{ }=-\frac{3}{2}+\sqrt{\frac{9}{4}+x}
$ $
它指定了每个的均衡X>0:
PURIFICATION|ECON经济作业代写ECONOMICS代考
3.4. 纯化。我们现在转向整个练习的核心。以上,我们发现了凯茜的混合均衡策略(23,13). 我们可以通过考虑重现这个策略X=0. 对于给定的X>0, Cathy 选择剧院的概率是
$$
\begin{aligned}
\theta_{C} &=\frac{x-\bar{t} {C}}{x}=\frac{x-\left(-\frac {3}{2}+\sqrt{\frac{9}{4}+x}\right)}{x} \ &=1-\frac{-\frac{3}{2}+\sqrt{\ frac{9}{4}+x}}{x}。\end{对齐}рH和r和,在和C一种nn○吨s你bs吨一世吨你吨和$X$F○r0b和C一种你s和吨H和n在和H一种v和$00$在H一世CH一世sn○吨d和F一世n和d.H○在和v和r,在和C一种n一种pp一世和d和一世′H○sp一世吨一种一世′sr你一世和在H一世CH一世s吨H和○r和米五一世一世一世.1(p.223):\begin{对齐} \lim {x \rightarrow 0}\left(1-\frac{-\frac{3}{2}+\sqrt{\frac{9}{4}+x}}{x}\右) &=\lim {x \rightarrow 0} 1-\lim {x \rightarrow 0} \frac{-\frac{3}{2}+\sqrt{\frac{9}{4}+x}} {x} \
&=1-\lim {x \rightarrow 0} \frac{\frac{1}{2 \sqrt{\frac{9}{4}+x}} \cdot 1}{1} \text {(德医院规则)} \ &=1-\lim {x \rightarrow 0} \frac{\frac{1}{2 \cdot \frac{3}{2}} \cdot 1}{1} \
&=\frac{2}{3}
\end{aligned}
$$
因此,Cathy 在静态贝叶斯博弈中的概率(取决于X) 收敛到矩阵博弈中的混合策略概率。由于 Cathy 选择了一个纯动作(取决于她的类型),替换为

matlab代写请认准UprivateTA™.
经济代写
计量经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
微观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写
宏观经济学代写请认准my-assignmentexpert™ Economics 经济学作业代写