MY-ASSIGNMENTEXPERT™可以为您提供math Math46400 Number theory 数论的代写代考和辅导服务!
这是纽约市立学院数论课程的代写成功案例。

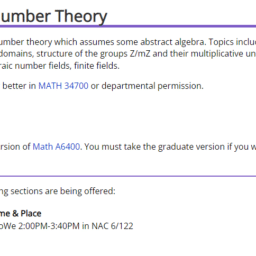
Math46400简介
A first course in algebraic number theory which assumes some abstract algebra. Topics include: unique factorization in the integers and Euclidean domains, structure of the groups Z/mZ and their multiplicative units, quadratic residues and quadratic reciprocity, algebraic number fields, finite fields.
Prerequisites: Grade of C or better in MATH 34700 or departmental permission.
Contact Hours: 4 hr./wk.
Credits: 4
This is an undergraduate version of Math A6400. You must take the graduate version if you want graduate credit.
Prerequisites
Number theory or arithmetic or higher arithmetic in older usage is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. German mathematician Carl Friedrich Gauss (1777–1855) said, “Mathematics is the queen of the sciences—and number theory is the queen of mathematics.”
Math46400 Number theory HELP(EXAM HELP, ONLINE TUTOR)
Let $K / \mathbb{F}_q(t)$ be a global function field, with $\mathbb{F}_q$ algebraically closed in $K$. The divisor group Div $K$ is the free abelian group generated by the places of $K$; it consists of formal sums $\sum_P n_P P$ over $P \in M_K$ in which only finitely many $n_P \in \mathbb{Z}$ are nonzero. This is the same as the group of $M_K$-divisors we defined in Lecture 15 , but here we view Div $K$ as an additive group and use $P$ to denote a place rather than $v$.
Corresponding to each $f \in K^{\times}$we have a principal divisor
$$
\operatorname{div}(f):=\sum_P \operatorname{ord}_P(f) P
$$
where $\operatorname{ord}_P: K^{\times} \rightarrow \mathbb{Z}$ is the discrete valuation corresponding to $P$, which we extend to Div $K$ by defining $\operatorname{ord}_P\left(\sum_P n_P P\right)=n_P$. Two divisors $D_1$ and $D_2$ are linearly equivalent if $D_1-D_2$ is a principal divisor, and we write $D_1 \sim D_2$ to indicate this; this defines an equivalence relation on Div $K$ and we use $[D]$ to denote the equivalence class of $D$.
The degree of a place $P$ is the dimension of the residue field of the local field $K_P$ as an $\mathbb{F}_q$-vector space; it extends to a group homomorphism deg: Div $K \rightarrow \mathbb{Z}$ whose kernel contains the subgroup of principal divisors (by the product formula); the corresponding quotient is denoted $\mathrm{Pic}^0 K$. The norm of a divisor $D$ is defined by $\mathrm{N}(D):=q^{\operatorname{deg} D}$; when $D=P$ this is the cardinality of the residue field and if $D$ is supported only on finite places this agrees with the absolute norm defined in Problem 2.
We partially order divisors by defining
$$
D_1 \leq D_2 \quad \Longleftrightarrow \quad \operatorname{ord}P\left(D_1\right) \leq \operatorname{ord}_P\left(D_2\right) \text { for all } P \in M_K \text {. } $$ A divisor $D \geq 0$ is said to be effective. The zeta function of $K$ is defined as a sum over effective divisors $$ \zeta_K(s):=\sum{D \geq 0} \mathrm{~N}(D)^{-s}=\sum_{D \geq 0} q^{-s \operatorname{deg}(D)}
$$
The Weil conjectures (for global function fields) concern three properties of $\zeta_K(s)$ :
$\zeta_K(s)$ is a rational function of $q^{-s}$.
There is a functional equation that relates $\zeta_K(1-s)$ and $\zeta_K(s)$.
The zeros of $\zeta_K(s)$ all lie on the line $\operatorname{Re}(s)=1 / 2$.
In this problem you will prove the first two; Weil proved the third in the 1940s, and a generalization to algebraic varieties of higher dimension conjectured by Weil was proved by Deligne in the 1970 s.
Associated to each divisor $D \in \operatorname{Div} K$ is a Riemann-Roch space
$$
L(D):=\left{f \in K^{\times}: \operatorname{div}(f) \geq-D\right} \cup{0}
$$
which is an $\mathbb{F}q$-vector space whose finite dimension we denote $\ell(D) \in \mathbb{Z}{\geq 0}$. The degree $\operatorname{deg} D$ and dimension $\ell(D)$ of a divisor $D$ depend only on the divisor class $[D]$ and are related by the following theorem (which you are not asked to prove).
Complete the following survey by rating each problem you attempted on a scale of 1 to 10 according to how interesting you found it ( 1 = “mind-numbing,” $10=$ “mind-blowing”), and how difficult you found it ( 1 = “trivial,” 10 = “brutal”). Also estimate the amount of time you spent on each problem to the nearest half hour.
\begin{tabular}{l|l|l|l|}
& Interest & Difficulty & Time Spent \
\hline Problem 1 & & & \
\hline Problem 2 & & & \
\hline Problem 3 & & & \
\hline Problem 4 & & & \
\hline Problem 5 & & & \
\hline
\end{tabular}
Please rate each of the following lectures that you attended, according to the quality of the material (1= “useless”, $10=$ “fascinating”), the quality of the presentation ( $1=$ “epic fail”, $10=$ “perfection”), the pace ( $1=$ “way too slow”, 10 =”way too fast”, $5=$ “just right”) and the novelty of the material to you ( $1=$ “old hat”, $10=$ “all new”).
\begin{tabular}{l|l|l|l|l|l|}
Date & Lecture Topic & Material & Presentation & Pace & Novelty \
\hline $11 / 8$ & The functional equation & & & & \
\hline $11 / 10$ & Dirichlet L-functions & & & & \
\hline
\end{tabular}
Please feel free to record any additional comments you have on the problem sets and the lectures, in particular, ways in which they might be improved.
These warmup exercises do not need to be written up or turned in, they are provided simply to help you check your understanding.
(a) Prove the nonarchimedean “triangle equality”: if $|\cdot|$ is a nonarchimedean absolute value on a field $k$ and $|x| \neq|y|$ then $|x+y|=\max (|x|,|y|)$.
(b) Prove that an absolute value $|\cdot|$ on a field $k$ is nonarchimedean if and only if $|n| \leq 1$ for all $n \in \mathbb{Z}_{>0}$ (view $n$ as an element of $k$ via the canonical ring homomorphism $\mathbb{Z} \rightarrow k$ ). (Hint: use the binomial theorem).
(c) Show that all absolute values on fields of positive characteristic are nonarchimedean, and all absolute values on finite fields are trivial.
(d) Write down a monic polynomial $f \in \mathbb{Z}[x]$ with $\sqrt{2}+\sqrt{3}$ as a root.
(a) Prove Ostrowski’s Theorem: every nontrivial absolute value on $\mathbb{Q}$ is equivalent to $|\cdot|p$ for some prime $p \leq \infty$. (b) Prove the product formula for $\mathbb{Q}$ : show that $\prod{p \leq \infty}|x|_p=1$ for all $x \in \mathbb{Q}^{\times}$.
(c) Determine the archimedean absolute values on $\mathbb{Q}(\sqrt{2})$ and $\mathbb{Q}(\sqrt{-2})$.

MY-ASSIGNMENTEXPERT™可以为您提供MATH MATH46400 NUMBER THEORY 数论的代写代考和辅导服务!