MY-ASSIGNMENTEXPERT™可以为您提供math Math46400 Number theory 数论的代写代考和辅导服务!
这是纽约市立学院数论课程的代写成功案例。

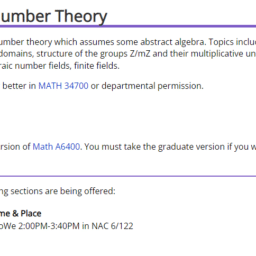
Math46400简介
A first course in algebraic number theory which assumes some abstract algebra. Topics include: unique factorization in the integers and Euclidean domains, structure of the groups Z/mZ and their multiplicative units, quadratic residues and quadratic reciprocity, algebraic number fields, finite fields.
Prerequisites: Grade of C or better in MATH 34700 or departmental permission.
Contact Hours: 4 hr./wk.
Credits: 4
This is an undergraduate version of Math A6400. You must take the graduate version if you want graduate credit.
Prerequisites
Number theory or arithmetic or higher arithmetic in older usage is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. German mathematician Carl Friedrich Gauss (1777–1855) said, “Mathematics is the queen of the sciences—and number theory is the queen of mathematics.”
Math46400 Number theory HELP(EXAM HELP, ONLINE TUTOR)
Prove that $1^3+2^3+\cdots+n^3=\left(\frac{n(n+1)}{2}\right)^2$, for all $n \geq 1$.
Solution:
We use induction. The base case is $n=1$ which is obvious:
$$
1=1^3=\left(\frac{1 \cdot 2}{2}\right)^2=1^2=1
$$
Now, let us prove the induction step. For this, assume that the result is true for some $n \geq 1$ and we need to prove that the result is true for $n+1$. Hence, we need to prove:
$$
1^3+2^3+\cdots+n^3+(n+1)^3=?\left(\frac{(n+1)(n+2)}{2}\right)^2
$$
This is indeed true because:
$$
\begin{aligned}
1^3+2^3+\cdots+n^3+(n+1)^3 & =\left(\frac{n(n+1)}{2}\right)^2+(n+1)^3 \
& =\frac{n^2(n+1)^2}{4}+(n+1)^3 \
& =(n+1)^2 \cdot\left(\frac{n^2}{4}+(n+1)\right) \
& =(n+1)^2 \cdot\left(\frac{n^2+4 n+4}{4}\right) \
& =\frac{(n+1)^2(n+2)^2}{4}=\left(\frac{(n+1)(n+2)}{2}\right)^2
\end{aligned}
$$
This proves the induction step. Hence, by the Principle of Mathematical Induction, the equality is true for all $n \geq 1$.
(a) Prove that, for all $n \geq 1$, we have:
$$
\frac{1}{1-x}=1+x+x^2+\cdots+x^{n-1}+\frac{x^n}{1-x} .
$$
(b) Prove that for all $n \geq 1,1+2+2^2+\cdots+2^{n-1}=2^n-1$.
Solution:
(a). We will use induction. The base case ( $n=1)$ is “trivial” = almost obvious:
$$
1+\frac{x}{1-x}=\frac{1-x+x}{1-x}=\frac{1}{1-x} .
$$
Now we prove the induction step. Suppose the equality is true for some $n \geq 1$ and we want to prove it for $n+1$. Since we can assume the equality for $n$, we also know that:
$$
\frac{1}{1-x}-\frac{x^n}{1-x}=1+x+x^2+\cdots+x^{n-1} .
$$
We will use the above equation below. At this point, it remains to verify the following equality:
$$
\frac{1}{1-x}={ }^? 1+x+x^2+\cdots+x^{n-1}+x^n+\frac{x^{n+1}}{1-x} .
$$
Let’s start working with the right hand side:
$$
\begin{aligned}
1+x+x^2+\cdots+x^{n-1}+x^n+\frac{x^{n+1}}{1-x} & =\frac{1}{1-x}-\frac{x^n}{1-x}+x^n+\frac{x^{n+1}}{1-x} \
& =\frac{1-x^n+x^n(1-x)+x^{n+1}}{1-x} \
& =\frac{1-x^n+x^n-x^{n+1}+x^{n+1}}{1-x}=\frac{1}{1-x}
\end{aligned}
$$
as desired. Hence, the induction step is proven, and by the Principle of Mathematical Induction, the equality is true for all $n \geq 1$.
(b). Now, plug $x=2$ in the equality we just prove to get:
$$
\frac{1}{1-2}=1+2+2^2+\cdots+2^{n-1}+\frac{2^n}{1-2}
$$
or
$$
2^n-1=1+2+2^2+\cdots+2^{n-1}
$$
as needed.
Prove that 5 divides $3^{4 n}-1$, for all $n \geq 1$.
Solution:
We use Induction. The base case, $n=1$ is clear since $3^4-1=80=5 \cdot 16$ is divisible by 5 . Now suppose that this property is true for some $n \geq 1$ and so, $3^{4 n}-1$ is divisible by 5 . Let us write then $3^{4 n}-1=5 k$ for some natural number $k \geq 1$. We need to prove that $3^{4(n+1)}-1$ is also divisible by 5 . But:
$$
3^{4 n+4}-1=3^4\left(3^{4 n}\right)-1=81(5 k+1)-1=405 k+81-1=405 k+80=5 \cdot(81 k+16) .
$$
Hence, $3^{4(n+1)}-1$ is also divisible by 5 . Hence, the induction step is proven, and by the Principle of Mathematical Induction, the property is true for all $n \geq 1$.
Prove that for any odd number $m \geq 1$, the number 9 divides $4^m+5^m$.
Solution:
Every odd number $m$ can be written as $2 n+1$, for some $n \geq 0$ (by the division theorem the remainder when dividing by 2 is 1 or 0 , and since $m$ is odd, it must be a remainder of 1). We use induction on $n$ to prove the result. The base case is trivial since $4+5=9$ is divisible by 9 . Suppose next that $n \geq 1$ is a number such that $4^{2 n+1}+5^{2 n+1}$ is divisible by 9 . Let us write $4^{2 n+1}+5^{2 n+1}=9 k$ for some $k \geq 1$. We shall show that $4^{2(n+1)+1}+5^{2(n+1)+1}$ is also divisible by 9 . Indeed:
$$
\begin{aligned}
4^{2 n+3}+5^{2 n+3} & =16 \cdot 4^{2 n+1}+25 \cdot 5^{2 n+1}=16\left(4^{2 n+1}+5^{2 n+1}\right)+9 \cdot 5^{2 n+1} \
& =16 \cdot 9 k+9 \cdot 5^{2 n+1}=9\left(16 k+5^{2 n+1}\right) .
\end{aligned}
$$
Hence, $4^{2(n+1)+1}+5^{2(n+1)+1}$ is also divisible by 9 . Hence, the induction step is proven, and by the Principle of Mathematical Induction, the property is true for all numbers $n \geq 1$, and so $4^m+5^m$ is divisible by 9 for all odd numbers $m \geq 1$. Notice that this property is not true for even $m$, e.g. $4^2+5^2=16+25=41$.

MY-ASSIGNMENTEXPERT™可以为您提供MATH MATH46400 NUMBER THEORY 数论的代写代考和辅导服务!