MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH3078 Partial Differential Equations偏微分方程的代写代考和辅导服务!
这是悉尼大学 偏微分方程的代写成功案例。
MATH3078课程简介
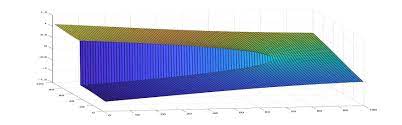
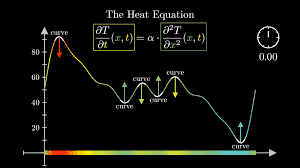
The aim of this unit is to introduce some fundamental concepts of the theory of partial differential equations (PDEs) arising in Physics, Chemistry, Biology and Mathematical Finance. The focus is mainly on linear equations but some important examples of nonlinear equations and related phenomena re introduced as well. After an introductory lecture, we proceed with first-order PDEs and the method of characteristics. Here, we also nonlinear transport equations and shock waves are discussed. Then the theory of the elliptic equations is presented with an emphasis on eigenvalue problems and their application to solve parabolic and hyperbolic initial boundary-value problems. The Maximum principle and Harnack’s inequality will be discussed and the theory of Green’s functions.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. demonstrating the ability to recognize different types of partial differential equations: “linear” or “nonlinear”, “order of the given equation”, “homogeneous” or “inhomogeneous”, and if it concerns 2nd-order equations, whether they are of “elliptic”, “parabolic”, or “hyperbolic” type
- LO2. demonstrating the conceptional understanding of how to apply different methods for solving different types of partial differential equations. Those methods include the use of classical ODE-concepts to solve PDEs
- LO3. understanding the definitions, main theorem, and corollaries of Green’s functions and Poisson kernel
- LO4. be fluent with “change of variable” into polar, cylindrical and spherically coordinates and to be able to compute partial derivatives in these coordinates
- LO5. develop an appreciation and strong working knowledge of the theory and application of elementary partial differential equations
- LO6. be fluent in using generalized Fourier transforms to solve parabolic and hyperbolic initial boundary value problems where the spatial variable might be of more than one variable
MATH3078 Partial Differential Equations HELP(EXAM HELP, ONLINE TUTOR)
Which of the following transformations are linear? If it is, find the matrix $A$ which implements the transformation.
a) $T\left[\begin{array}{l}x \ y\end{array}\right]=\left[\begin{array}{c}2 y \ 3 x \ x\end{array}\right]$
b) $T\left[\begin{array}{l}x \ y \ z\end{array}\right]=\left[\begin{array}{l}x+2 \ y+3 \ z-3\end{array}\right]$
c) $T\left[\begin{array}{l}x \ y\end{array}\right]=\left[\begin{array}{c}y+2 x-\sin (x) \ x\end{array}\right]$
d) $T\left[\begin{array}{l}x \ y \ z\end{array}\right]=[-x-y]$
e) $T\left[\begin{array}{l}x \ y \ z\end{array}\right]=\left[\begin{array}{l}y+x \ z-x\end{array}\right]$
Find the inverse of the following linear transformations $x \rightarrow A x$ or state that it is not invertible
a) $A=\left[\begin{array}{ll}1 & 2 \ 3 & 2\end{array}\right]$
b) $A=\left[\begin{array}{ll}2 & 0 \ 0 & 2\end{array}\right]$
c) $A=\left[\begin{array}{ll}0 & 1 \ 1 & 0\end{array}\right]$
d) $A=\left[\begin{array}{cc}3 & -2 \ -6 & 4\end{array}\right]$
e) Verify that $\left[\begin{array}{cc}d & -b \ -c & a\end{array}\right] /(a d-b c)$ is the inverse of $A=\left[\begin{array}{ll}a & b \ c & d\end{array}\right]$ if $a d \neq b c$.
We learn how to invert a matrix later. For now, get the inverse by solving $A x=e_k$, rendering the $k$ ‘th column of $A^{-1}$.
For each of the matrices, sketch the effect of the linear transformation $T(x)=A x$ on the face.
a) $\left[\begin{array}{cc}0 & -1 \ 1 & 0\end{array}\right]$
b) $\left[\begin{array}{ll}2 & 0 \ 0 & 2\end{array}\right]$.
c) $\left[\begin{array}{ll}0 & 1 \ 1 & 0\end{array}\right]$
d) $\left[\begin{array}{cc}1 & 0 \ 0 & -1\end{array}\right]$
e) $\left[\begin{array}{ll}1 & 0 \ 0 & 2\end{array}\right]$
a) Let $v=\left[\begin{array}{l}v_1 \ v_2 \ v_3\end{array}\right]$. Which matrix $A$ implements the transformation
$$
x=\left[\begin{array}{l}
x_1 \
x_2 \
x_3
\end{array}\right] \rightarrow v \times x=\left[\begin{array}{c}
v_2 x_3-v_3 x_2 \
v_3 x_1-v_1 x_3 \
v_1 x_2-v_2 x_1
\end{array}\right] .
$$
b) Which matrix $A$ implements the transformation
$$
x=\left[\begin{array}{l}
x_1 \
x_2 \
x_3
\end{array}\right] \rightarrow v \cdot x=\left[v_1 x_1+v_2 x_2+v_3 x_3\right] ?
$$
Find the linear transformation which rotates counterclockwise in the plane by $3 \pi / 4$. Do that by drawing the images of the vectors $e_1=\left[\begin{array}{l}1 \ 0\end{array}\right]$ and $e_2=\left[\begin{array}{l}0 \ 1\end{array}\right]$ and using these vectors to build the matrix.
MY-ASSIGNMENTEXPERT™可以为您提供SYDNEY MATH3078 PARTIAL DIFFERENTIAL EQUATIONS偏微分方程的代写代考和辅导服务!