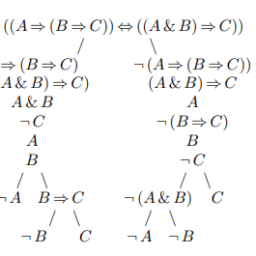数学代写|MATH455 Mathematical Logic

MY-ASSIGNMENTEXPERT™可以为您提供 hawaii MATH455 Mathematical Logic数理逻辑的代写代考和辅导服务！

这是夏威夷大学 数理逻辑的代写成功案例。

MATH455课程简介

A system of first order logic. Formal notions of well-formed formula, proof, and derivability. Semantic notions of model, truth, and validity. Completeness theorem. Pre: 321 or graduate standing in a related field or consent. Recommended: 454.Mathematical logic is the study of formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory. Research in mathematical logic commonly addresses the mathematical properties of formal systems of logic such as their expressive or deductive power. However, it can also include uses of logic to characterize correct mathematical reasoning or to establish foundations of mathematics.

Prerequisites 

Since its inception, mathematical logic has both contributed to and been motivated by the study of foundations of mathematics. This study began in the late 19th century with the development of axiomatic frameworks for geometry, arithmetic, and analysis. In the early 20th century it was shaped by David Hilbert’s program to prove the consistency of foundational theories. Results of Kurt Gödel, Gerhard Gentzen, and others provided partial resolution to the program, and clarified the issues involved in proving consistency. Work in set theory showed that almost all ordinary mathematics can be formalized in terms of sets, although there are some theorems that cannot be proven in common axiom systems for set theory. Contemporary work in the foundations of mathematics often focuses on establishing which parts of mathematics can be formalized in particular formal systems (as in reverse mathematics) rather than trying to find theories in which all of mathematics can be developed.

MATH455 Mathematical Logic HELP（EXAM HELP， ONLINE TUTOR）

Solutions.
(a) Let $E_n$ be sentence in the language with only the identity predicate $I$, saying that the universe consists of exactly $n$ elements. (Details of $E_n$ are in Exercise 4.1.10 of the lecture notes.) If $X=\left{n_1, \ldots, n_k\right}$, then $X$ is the spectrum of $E_{n_1} \vee \cdots \vee E_{n_k}$, and the complement of $X$ is spectrum of
$$
\neg\left(E_{n_1} \vee \cdots \vee E_{n_k}\right) .
$$
(b) The even numbers are the spectrum of a sentence which says: $R$ is an equivalence relation on the universe, such that each equivalence class consists of exactly two elements. For more details, see Exercise 4.1.16 in the lecture notes.
(c) The odd numbers are the spectrum of a sentence which says: $R$ is an equivalence relation on the universe, such that each equivalence class consists of exactly two elements, except for one equivalence class, which consists of exactly one element.
(d) We may assume that $0 \leq r0$, the set
$$
{n \geq 1: n \equiv r \bmod m}={n \geq 1: m \text { divides } n \text { with remainder } r}
$$
is the spectrum of a sentence which says: $R$ is an equivalence relation on the universe, such that each equivalence class consists of exactly $m$ elements, except for one equivalence class, which consists of exactly $r$ elements.
(e) Assume that $X$ is the spectrum of $A$ and $Y$ is the spectrum of $B$. Then $X \cup Y$ is the spectrum of $A \vee B$. Also, $X \cap Y$ is the spectrum of $A \& B$, provided $A$ and $B$ have no predicates in common except the identity predicate. To arrange for this, replace $B$ by an analogous sentence in a different language.

Solution.
Let $Z$ be as in Exercise 2 above. For each of the given sets $X$, we exhibit a sentence $A$ with the following properties: $X$ is the spectrum of $Z \& A$, and the complement of $X$ is the spectrum of $Z \& \neg A$.
(a) $\exists z((\neg \exists w R z w) \&(\neg \exists x \exists y(R x z \& R y z \& Q x y z)) \&(\neg O z))$.
(b) $\exists z((\neg \exists w R z w) \& \exists x Q x x z)$.
(c) $\exists z \exists v((\neg \exists w R z w) \&(\exists u(O u \& S u v))$ $\& \forall x((\neg O x \& \exists y Q x y z) \Rightarrow \exists w Q v w x))$.
(d) $\exists z \exists v((\neg \exists w R z w) \&(\neg \exists x \exists y(R x v \& R y v \& Q x y v)) \&(\neg O v)$ $\& \forall x((\neg O x \& \exists y Q x y z) \Rightarrow \exists w Q v w x))$.

Solution.
As $Z$ we may take the conjunction of the following clauses.
(a) $\forall x \forall y(R x y \vee R y x \vee I x y)$
(b) $\forall x \forall y(R x y \Rightarrow \neg R y x)$
(c) $\forall x \forall y \forall z((R x y \& R y z) \Rightarrow R x z)$
(d) $\forall x \forall z(S x z \Leftrightarrow(R x z \& \neg \exists y(R x y \& R y z)))$
(e) $\forall u(O u \Leftrightarrow \neg \exists x R x u)$
(f) $\forall u(O u \Rightarrow \forall x \forall z(P u x z \Leftrightarrow S x z))$
(g) $\forall v \forall w(S v w \Rightarrow \forall x \forall z(P w x z \Leftrightarrow \exists y($ Syz \& Pvxy $))$
(h) $\forall u(O u \Rightarrow \forall x \forall z(Q u x z \Leftrightarrow I x z))$
(i) $\forall v \forall w(S v w \Rightarrow \forall x \forall z(Q w x z \Leftrightarrow \exists y(Q v x y \& P x y z)))$
Clauses (a), (b) and (c) say that $R$ is an irreflexive linear ordering of the universe. Clause (d) says that $S$ is the immediate successor relation, with respect to $R$. Clause (e) says that 1 is the first element of the universe, with respect to $R$. Clauses (f) and (g) define the addition predicate $P$, by induction along $R$, in terms of $S$. Clauses (h) and (i) define the multiplication predicate $Q$, by induction along $R$, in terms of $S$ and $P$.

Solution. Left to the student

MY-ASSIGNMENTEXPERT™可以为您提供 HAWAII MATH455 MATHEMATICAL LOGIC数理逻辑的代写代考和辅导服务！