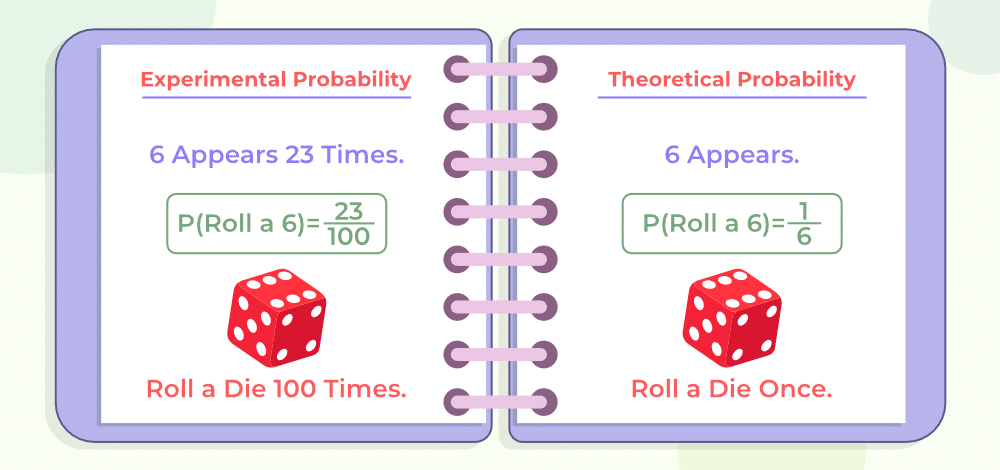
MY-ASSIGNMENTEXPERT™可以为您提供sydney STAT2011 Probability Theory概率论课程的代写代考和辅导服务!
这是悉尼大学概率论课程的代写成功案例。
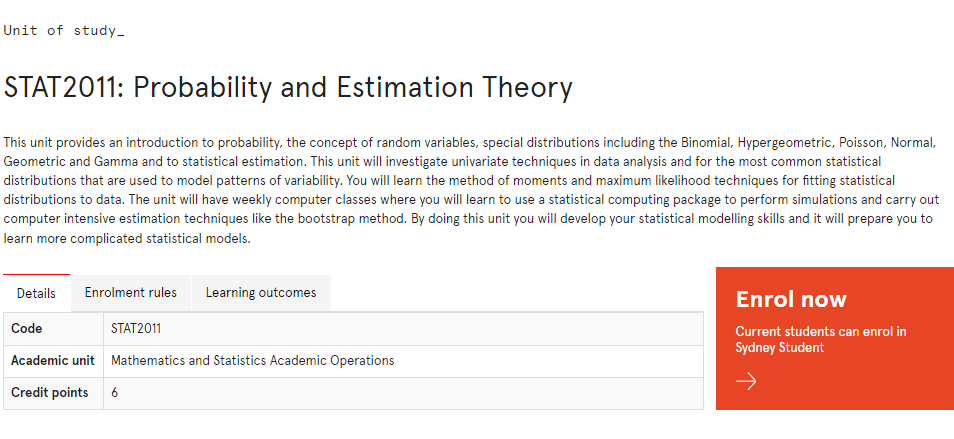
STAT2011课程简介
This unit provides an introduction to probability, the concept of random variables, special distributions including the Binomial, Hypergeometric, Poisson, Normal, Geometric and Gamma and to statistical estimation. This unit will investigate univariate techniques in data analysis and for the most common statistical distributions that are used to model patterns of variability. You will learn the method of moments and maximum likelihood techniques for fitting statistical distributions to data. The unit will have weekly computer classes where you will learn to use a statistical computing package to perform simulations and carry out computer intensive estimation techniques like the bootstrap method. By doing this unit you will develop your statistical modelling skills and it will prepare you to learn more complicated statistical models.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. construct appropriate statistical models involving random variables for a range of modelling scenarios. Compute (or approximate with a computer if necessary) numerical characteristics of random variables in these models such as probabilities, expectations and variances
- LO2. fit such models in outcome 1. to data (as appropriate) by estimating any unknown parameters
- LO3. compute appropriate (both theoretically and computationally derived) measures of uncertainty for any parameter estimates
- LO4. assess the goodness of fit (as appropriate) of a fitted model
- LO5. apply certain mathematical results (e.g. inequalities, limiting results) to problems relating to statistical estimation theory
- LO6. prove certain mathematical results (e.g. inequalities, limiting results) used in the course.
STAT2011 Probability Theory HELP(EXAM HELP, ONLINE TUTOR)
(a). Show that with probability 1 , Brownian motion is not 0 throughout a time interval of positive length.
(b). Show that with probability 1 , Brownian motion is not constant on a time interval of positive length.
Show using the Kolmogorov 0-1 Law that with probability 1, Brownian motion takes both positive and negative values in every interval around the time point 0 .
Show that for every $\epsilon>0$, there exists a $\delta>0$ such that $P\left(B_t\right.$ hits location $-\delta$ before location 1$) \geq 1-\epsilon$
Let $X$ be an exponential distribution. How does one normalize the conditional distribution of $X$ given $X \geq n$ to get a nontrivial limit (as $n \rightarrow \infty)$ and what is this limiting distribution?
Let $Z$ be a standard normal distribution. How does one normalize the conditional distribution of $Z$ given $Z \geq n$ to get a nontrivial limit (as $n \rightarrow \infty)$ and what is this limiting distribution?
a. Show that for any random variable $X$, there exist random variables $\left{X_n\right}$ whose distributions are continuous so that $X_n$ converges to $X$ in distribution.
b. Show that for any random variable $X$ with a continuous distribution, there exist random variables $\left{X_n\right}$ each of which takes on only finitely many values so that $X_n$ converges to $X$ in distribution. (This is true for any random variable $X$ but doing it in general might be a little “meckig”.)
MY-ASSIGNMENTEXPERT™可以为您提供sydney STAT2011 Probability Theory概率论课程的代写代考和辅导服务!