MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH3979 Complex Analysis复分析的代写代考和辅导服务!
这是悉尼大学复分析课程的代写成功案例。
MATH3979课程简介
This unit continues the study of functions of a complex variable introduced in the second year unit Analysis (MATH2023/2923). It is aimed at highlighting certain topics from analytic function theory that have wide applications and intrinsic beauty. By learning about the analysis of functions of a complex variable, you will acquire a very important background for mathematical areas such as dynamics, algebraic and differential geometry, and number theory; and advanced theoretical physics such as quantum mechanics, string theory, and quantum field theory. The unit will begin with a revision of properties of complex numbers and complex functions. This will be followed by material on conformal mappings, Riemann surfaces, complex integration, entire and analytic functions, the Riemann mapping theorem, analytic continuation, and Gamma and Zeta functions. Finally, special topics chosen by the lecturer will be presented, which may include elliptic functions, normal families, Julia sets, functions of several complex variables, or complex manifolds. At the end of this unit you will have received a broad introduction and gained a variety of tools to apply them within your further mathematical studies and/or in other disciplines.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. demonstrate a conceptual understanding of limit, continuity, differentiation, and integration as well as a thorough background in variety of techniques and applications of complex analysis
- LO2. assess problems in the framework of complex analysis, to choose among several potentially appropriate mathematical methods of solution, and persist in the face of difficulty
- LO3. present complete and mathematically rigorous solutions for problems in complex analysis that include appropriate justification for their reasoning
- LO4. recognise problems in mathematics, science, engineering and real life that are amenable to complex analysis, and to formulate models for such problems and apply the techniques of complex analysis in solving them
MATH3979 Complex Analysis HELP(EXAM HELP, ONLINE TUTOR)
Let $r, s, \theta, \phi$ be real. Let
$$
\begin{aligned}
z & =r(\cos \theta+\mathrm{i} \sin \theta) \
w & =s(\cos \phi+\mathrm{i} \sin \phi)
\end{aligned}
$$
Form the product $z w$ and use the standard formulas for $\cos (\theta+\phi), \sin (\theta+\phi)$ to show that $\arg (z w)=\arg (z)+\arg (w)$ (for any values of arg on the right, and some value of arg on the left).
By induction on $n$, derive De Moivre’s Theorem
$$
(\cos \theta+\mathrm{i} \sin \theta)^n=\cos n \theta+\mathrm{i} \sin n \theta
$$
for all natural numbers $n$.
Specialise to the case $n=3$ and recover the usual formulas for $\cos 3 \theta$ and $\sin 3 \theta$ in terms of $\cos \theta$ and $\sin \theta$.
Use De Moivre’s Theorem (Exercise 8) and the substitution $z=r(\cos \theta+\mathrm{i} \sin \theta)$ to show that the equation $z^3=1$ has three distinct complex roots. Find them.
Compute the square roots of $1+i \sqrt{3}, \sqrt{3}-i$, and $1+i$, and the cube roots of $\sqrt{3}+i, 1-i$, i. Sketch these points in the complex plane.
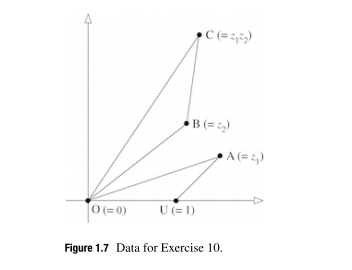
In earlier textbooks, multiplication of complex numbers is often defined as follows. Given two complex numbers $z_1, z_2$, represent them by points A and B in the complex plane; and let $\mathrm{O}, \mathrm{U}$ be the points $z=0,1$ respectively, Figure 1.7.
Draw triangle $\mathrm{OBC}$ similar to triangle OUA (where $\angle \mathrm{BOC}=\angle \mathrm{UOA}, \angle \mathrm{OBC}=$ $\angle \mathrm{OUA})$. Then $z_1 z_2$ is represented by the point $\mathrm{C}$ so constructed.
Using the fact that $\left|z_1 z_2\right|=\left|z_1\right|\left|z_2\right|$, and the result of Exercise 5, show that this construction agrees with our definition (1.2).
Define a square root $\sqrt{z}$ of a complex number $z$ to be any complex number $w$ such that $w^2=z$. Prove that every non-zero complex number has exactly two square roots, and give formulas for them in terms of re $z$ and im $z$.
If $a, b, c \in \mathbb{C}$ with $a \neq 0$, show that the solutions of the quadratic equation
$$
a z^2+b z+c=0
$$
are precisely
$$
z=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}
$$
Define a $k$ th root $\sqrt[k]{z}$ to be any $w$ such that $w^k=z$. Use De Moivre’s Theorem to find an expression for $\sqrt[k]{r(\cos \theta+i \sin \theta)}$.
MY-ASSIGNMENTEXPERT™可以为您提供sydney MATH3979 Complex Analysis复分析的代写代考和辅导服务!