如果你也在 怎样代写密码学cryptography这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。密码学cryptography是在存在对抗行为的情况下安全通信技术的实践和研究。 更广泛地说,密码学是关于构建和分析防止第三方或公众阅读私人信息的协议;[信息安全的各个方面,如数据保密性、数据完整性、认证和不可抵赖性,是现代密码学的核心。现代密码学存在于数学、计算机科学、电子工程、通信科学和物理学等学科的交叉点。密码学的应用包括电子商务、基于芯片的支付卡、数字货币、计算机密码和军事通信。
密码学cryptography实际上是加密的同义词,将信息从可读状态转换为不可理解的废话。加密信息的发送者只与预期的接收者分享解码技术,以排除对手的访问。密码学文献通常用Alice(”A”)代表发送者,Bob(”B”)代表预定接收者,Eve(”窃听者”)代表对手。 自从第一次世界大战中转子密码机的发展和第二次世界大战中计算机的出现,密码学方法变得越来越复杂,其应用也越来越多。
my-assignmentexpert™ 密码学cryptography作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的密码学cryptography作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此密码学cryptography作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的密码学cryptography代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种密码学cryptography相关的作业也就用不着 说。
我们提供的密码学cryptography及其相关学科的代写,服务范围广, 其中包括但不限于:

数学代写|密码学作业代写cryptography代考|Formal Languages and Regular Expressions
Formally, a language is a set of words. A word is a finite sequence of characters taken from an alphabet. An alphabet is a finite set $\Sigma$. The basic operation defined on words is concatenation. Given two words $u$ and $v$, we let $u | v$ denote the concatenation of $u$ and $v$. We can thus let word denote the word $(\mathrm{w}, \circ, \mathrm{r}, \mathrm{d})$ as the concatenation of four elementary words which consist of single characters. We also define the length of a word which is its number of characters. The length is additive with concatenation (the length of a concatenated word is the sum of the lengths of concatenatees). A special word is the null word $\varepsilon$ of length zero. We have the property that $u|\varepsilon=\varepsilon| u=u$ for any word $u$. Concatenation in the set of all words over the alphabet $\Sigma$ is thus an associative law for which $\varepsilon$ is a neutral element. It is also regular: $u|v=u| w$ or $v|u=w| u$ implies $v=w$ for any words $u, v, w$.
Alphabets of cardinality 1 are used in order to represent integers: if $\Sigma={1}$, five is represented in unary by 11111. In many cases, we use the binary alphabet $\Sigma={0,1}$.
数学代写|密码学作业代写CRYPTOGRAPHY代考|Finite Automata
A finite automaton consists of
- a finite set $Q$ of states,
- a particular state $q_{0} \in Q$ called the initial state,
- a particular subset $F \subseteq Q$ of final states,
- a finite set $\Sigma$ called the input alphabet,
- a function $\delta$ from $Q \times \Sigma$ to $Q$ called the transition function.
We recursively extend the $\delta$ function on $Q \times \Sigma^{*}$ by
$$
\delta(q, \varepsilon)=q
$$
and
$$
\delta(q, u | a)=\delta(\delta(q, u), a)
$$
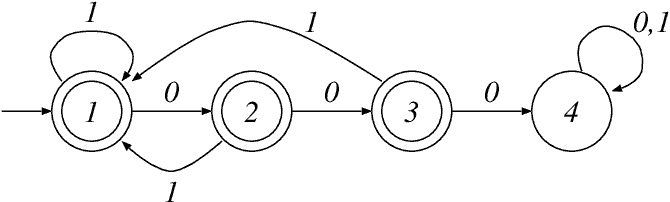
If a word $u$ is such that $\delta\left(q_{0}, u\right) \in F$, we say that $u$ is accepted by the automaton. The set of all accepted words is the language accepted by the automaton.
数学代写|密码学作业代写CRYPTOGRAPHY代考|Beyond Finite Automata Capabilities
Finite automata do some computations in very simple ways. The output of the computation is the information whether the input word is accepted or not. Regular languages are thus a nice notion of simple computation. It is however not complete because many simple languages are not regular, thus not accepted by finite automata, as shown by the following result.
The set of all $0^{i} 1^{i}$ words for $i \geq 0$ is not a regular language.
Proof. Let $\mathcal{A}=\left(Q, q_{0}, F, \delta\right)$ be a finite automaton which accepts this language, and let us look for a contradiction. For any $i$, we let $q_{i}$ be $\delta\left(q_{0}, 0^{i}\right)$. Obviously, $\delta\left(q_{i}, 1^{i}\right)$ is a final state. But since $0^{i} 1^{j}$ is not accepted for $i \neq j$, all $q_{i}$ must be pairwise different. Hence we have an infinite sequence of states $q_{0}, q_{1}, \ldots$, which is not possible for finite automata.
Finite automata could have been thought of as a good model for computation since all computers are indeed finite automata. What the above result shows is that $0^{i} 1^{i}$ cannot be recognized when $i$ is very long, especially when it is much longer than what the computer can store. Therefore this notion does not scale. Furthermore, the finite automaton model does not capture the intuitive notion of complexity since the transition function can be very expensive to implement. This is why we need another model.
密码学代写
数学代写|密码学作业代写CRYPTOGRAPHY代考|FORMAL LANGUAGES AND REGULAR EXPRESSIONS
形式上,语言是一组词。单词是从字母表中提取的有限字符序列。字母表是有限集Σ. 对单词定义的基本操作是连接。给定两个词在和在,我们让在|在表示的串联在和在. 因此我们可以让 word 表示这个词(在,∘,r,d)作为由单个字符组成的四个基本单词的串联。我们还定义了一个单词的长度,即它的字符数。长度与串联相加吨H和l和nG吨H这F一种C这nC一种吨和n一种吨和d在这rd一世s吨H和s在米这F吨H和l和nG吨Hs这FC这nC一种吨和n一种吨和和s. 特殊词是空词e长度为零。我们拥有的财产在|e=e|在=在对于任何词在. 字母表上所有单词的集合中的连接Σ因此是一个结合律e是中性元素。这也是常规的:在|在=在|在或者在|在=在|在暗示在=在对于任何话在,在,在.
基数为 1 的字母用于表示整数:如果Σ=1, 5 用 11111 一元表示。在很多情况下,我们使用二进制字母表Σ=0,1.
数学代写|密码学作业代写CRYPTOGRAPHY代考|FINITE AUTOMATA
一个有限自动机包括
- 有限集问各州,
- 特定状态q0∈问称为初始状态,
- 一个特定的子集F⊆问最终状态,
- 有限集Σ称为输入字母表,
- 一个函数d从问×Σ到问称为转移函数。
我们递归地扩展d功能开启问×Σ∗经过
d(q,e)=q
和
d(q,在|一种)=d(d(q,在),一种)
如果一句话在是这样的d(q0,在)∈F, 我们说在被自动机接受。所有接受词的集合就是自动机接受的语言。
数学代写|密码学作业代写CRYPTOGRAPHY代考|BEYOND FINITE AUTOMATA CAPABILITIES
有限自动机以非常简单的方式进行一些计算。计算的输出是输入词是否被接受的信息。因此,正则语言是简单计算的一个很好的概念。然而它并不完整,因为许多简单的语言不是规则的,因此不被有限自动机接受,如下面的结果所示。
所有的集合0一世1一世的话一世≥0不是常规语言。
证明。让一种=(问,q0,F,d)是一个接受这种语言的有限自动机,让我们寻找矛盾。对于任何一世,我们让q一世是d(q0,0一世). 明显地,d(q一世,1一世)是最终状态。但由于0一世1j不被接受一世≠j, 全部q一世必须成对不同。因此我们有无限的状态序列q0,q1,…,这对于有限自动机是不可能的。
有限自动机可以被认为是一个很好的计算模型,因为所有计算机确实都是有限自动机。上述结果表明0一世1一世无法识别时一世很长,尤其是当它比计算机可以存储的时间长得多时。因此,这个概念无法扩展。此外,有限自动机模型没有捕捉到复杂性的直观概念,因为转换函数的实现可能非常昂贵。这就是为什么我们需要另一个模型。

数学代写|密码学作业代写cryptography代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。