如果你也在 怎样代写信号和系统signals and systems这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。信号和系统signals and systems信号是对一个参数如何随另一个参数变化的描述。例如,电子电路中电压随时间变化,或图像中亮度随距离变化。一个系统是任何对输入信号产生输出信号的过程。
信号和系统signals and systems是对模拟和数字信号处理的介绍,这一主题构成了许多不同领域的工程系统的一个组成部分,包括地震数据处理、通信、语音处理、图像处理、国防电子、消费电子和消费产品。
my-assignmentexpert™ 信号和系统signals and systems作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的信号和系统signals and systems作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此信号和系统signals and systems作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在信息Information作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的信号和系统signals and systems代写服务。我们的专家在信息Information代写方面经验极为丰富,各种信号和系统signals and systems相关的作业也就用不着 说。
我们提供的信号和系统signals and systems及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
信号代写|信号和系统作业代写signals and systems代考|Representation of LTIC systems
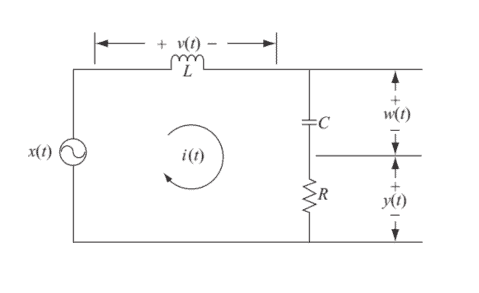
For a linear CT system, the relationship between the applied input $x(t)$ and output $y(t)$ can be described using a linear differential equation of the following form:
$$
\begin{aligned}
&\frac{\mathrm{d}^{n} y}{\mathrm{~d} t^{n}}+a_{n-1} \frac{\mathrm{d}^{n-1} y}{\mathrm{~d} t^{n-1}}+\cdots+a_{1} \frac{\mathrm{d} y}{\mathrm{~d} t}+a_{0} y(t) \
&\quad=b_{m} \frac{\mathrm{d}^{m} x}{\mathrm{~d} t^{m}}+b_{m-1} \frac{\mathrm{d}^{m-1} x}{\mathrm{~d} t^{m-1}}+\cdots+b_{1} \frac{\mathrm{d} x}{\mathrm{~d} t}+b_{0} x(t)
\end{aligned}
$$
where coefficients $a_{k}$, for $0 \leq k \leq(n-1)$, and $b_{k}$, for $0 \leq k \leq m$, are parameters characterized by the linear system. If the linear system is also time-invariant, then the $a_{k}$ and $b_{k}$ coefficients are constants. We will use the compact notation $\dot{y}$ to denote the first derivative of $y(t)$ with respect to $t$. Thus $\dot{y}=\mathrm{d} y / \mathrm{d} t, \ddot{y}=$ $\mathrm{d}^{2} y / \mathrm{d} t^{2}$, and so on for the higher derivatives. We now consider an electrical circuit that is modeled by a differential equation.
信号代写|信号和系统作业代写signals and systems代考|Representation of signals using Dirac delta functions
In this section we will show that any arbitrary signal $x(t)$ can be represented as a linear combination of time-shifted impulse functions. To illustrate our result, we define a new function $\delta_{\Delta}(t)$ as follows:
$$
\delta_{\Delta}(t)= \begin{cases}1 / \Delta & 0<t<\Delta \ 0 & \text { otherwise }\end{cases}
$$
The waveform for $\delta_{\Delta}(t)$ is shown in Fig. 3.3(a); it resembles that of a rectangular pulse with width $\Delta$ and height $1 / \Delta$. To approximate $x(t)$ as a linear combination of $\delta_{\Delta}(t)$, the time axis is divided into uniform intervals of duration $\Delta$. Within a time interval of duration $\Delta$, say $k \Delta<t<(k+1) \Delta, x(t)$ is approximated by a constant value $x(k \Delta) \delta_{\Delta}(t-k \Delta) \Delta$. Following the aforementioned procedure for the entire time axis, $x(t)$ can be approximated as follows:
$$
\begin{aligned}
\hat{x}(t)=& \cdots+x(-k \Delta) \delta_{\Delta}(t+k \Delta) \cdot \Delta+\cdots+x(-\Delta) \delta_{\Delta}(t+\Delta) \cdot \Delta \
&+x(0) \delta_{\Delta}(t) \cdot \Delta+x(\Delta) \delta_{\Delta}(t-\Delta) \cdot \Delta+\cdots \
&+x(k \Delta) \delta_{\Delta}(t-k \Delta) \cdot \Delta+\cdots,
\end{aligned}
$$
which is shown as the staircase waveform in Fig. 3.3(b). For a given value of $t$, say $t=m \Delta$, only one term $(k=m)$ on the right-hand side of Eq. (3.21) is nonzero. This is because only one of the shifted functions $\delta_{\Delta}(t-k \Delta)$ corresponding to $k=m$ is non-zero. Therefore, a more compact representation for Eq. (3.21) is obtained by using the following summation:
$$
\hat{x}(t)=\sum_{k=-\infty}^{\infty} x(k \Delta) \delta_{\Delta}(t-k \Delta) \Delta .
$$
信号代写|信号和系统作业代写SIGNALS AND SYSTEMS代考|Impulse response of a system
In Section 3.1, a constant-coefficient differential equation is used to specify the input-output characteristics of an LTIC system. An alternative representation of an LTIC system can be obtained by specifying its impulse response. In this section, we will formally define the impulse response and illustrate how the impulse response of an LTIC system can be derived directly from the differential equation modeling the LTIC system.
Definition 3.1 The impulse response h(t) of an LTIC system is the output of the system when a unit impulse $\delta(t)$ is applied at the input. Following the notation introduced in Eq. (2.1), the impulse response can be expressed as
$$
\delta(t) \rightarrow h(t)
$$
with zero initial conditions. Because the system is LTIC, it satisfies the linearity and the time-shifting properties. If the input is a scaled and time-shifted impulse function $a \delta\left(t-t_{0}\right)$, the output, Eq. (3.25), of the system is also scaled by the factor of a and is time-shifted by $t_{0}$, i.e.
$$
a \delta\left(t-t_{0}\right) \rightarrow a h\left(t-t_{0}\right)
$$
for any arbitrary constants $a$ and $t_{0}$.
信号和系统代写
信号代写|信号和系统作业代写SIGNALS AND SYSTEMS代考|REPRESENTATION OF LTIC SYSTEMS
对于线性 CT 系统,施加输入之间的关系X(吨)和输出是(吨)可以使用以下形式的线性微分方程来描述:
dn是 d吨n+一种n−1dn−1是 d吨n−1+⋯+一种1d是 d吨+一种0是(吨) =b米d米X d吨米+b米−1d米−1X d吨米−1+⋯+b1dX d吨+b0X(吨)
其中系数一种ķ, 为了0≤ķ≤(n−1), 和bķ, 为了0≤ķ≤米, 是由线性系统表征的参数。如果线性系统也是时不变的,那么一种ķ和bķ系数是常数。我们将使用紧凑符号是˙表示的一阶导数是(吨)关于吨. 因此是˙=d是/d吨,是¨= d2是/d吨2, 等等更高阶的导数。我们现在考虑一个由微分方程建模的电路。
信号代写|信号和系统作业代写SIGNALS AND SYSTEMS代考|REPRESENTATION OF SIGNALS USING DIRAC DELTA FUNCTIONS
在本节中,我们将展示任何任意信号X(吨)可以表示为时移脉冲函数的线性组合。为了说明我们的结果,我们定义了一个新函数dΔ(吨)如下:
dΔ(吨)={1/Δ0<吨<Δ 0 除此以外
波形为dΔ(吨)如图 3.3 所示一种; 它类似于一个具有宽度的矩形脉冲Δ和身高1/Δ. 近似X(吨)作为一个线性组合dΔ(吨), 时间轴被划分为均匀的持续时间区间Δ. 在持续时间的时间间隔内Δ, 说ķΔ<吨<(ķ+1)Δ,X(吨)由一个常数值近似X(ķΔ)dΔ(吨−ķΔ)Δ. 按照前面提到的整个时间轴的过程,X(吨)可以近似如下:
X^(吨)=⋯+X(−ķΔ)dΔ(吨+ķΔ)⋅Δ+⋯+X(−Δ)dΔ(吨+Δ)⋅Δ +X(0)dΔ(吨)⋅Δ+X(Δ)dΔ(吨−Δ)⋅Δ+⋯ +X(ķΔ)dΔ(吨−ķΔ)⋅Δ+⋯,
如图 3.3 中的阶梯波形所示b. 对于给定的值吨, 说吨=米Δ, 只有一项(ķ=米)在等式的右侧。3.21是非零的。这是因为只有一个移位函数dΔ(吨−ķΔ)对应于ķ=米非零。因此,方程式更紧凑的表示。3.21通过使用以下总和获得:
X^(吨)=∑ķ=−∞∞X(ķΔ)dΔ(吨−ķΔ)Δ.
信号代写|信号和系统作业代写SIGNALS AND SYSTEMS代考|IMPULSE RESPONSE OF A SYSTEM
在 3.1 节中,常数系数微分方程用于指定 LTIC 系统的输入输出特性。LTIC 系统的另一种表示可以通过指定其脉冲响应来获得。在本节中,我们将正式定义脉冲响应,并说明如何从 LTIC 系统建模的微分方程直接推导出 LTIC 系统的脉冲响应。
定义 3.1 脉冲响应 h吨一个 LTIC 系统的输出是当一个单位脉冲时系统的输出d(吨)应用于输入。遵循方程式中引入的符号。2.1,脉冲响应可以表示为
d(吨)→H(吨)
初始条件为零。因为系统是LTIC,它满足线性和时移特性。如果输入是一个缩放和时移的脉冲函数一种d(吨−吨0),输出,等式。3.25, 系统也按 a 的因子缩放并且时移吨0, IE
一种d(吨−吨0)→一种H(吨−吨0)
对于任意常数一种和吨0.

信号代写|信号和系统作业代写signals and systems代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。