如果你也在 怎样代写网络安全network security这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。网络安全network security是一套技术，通过防止各种潜在威胁进入或在网络中扩散，来保护公司基础设施的可用性和完整性。

网络安全network security一个网络安全架构是由保护网络本身和在网络上运行的应用程序的工具组成。有效的网络安全策略采用了可扩展和自动化的多道防线。每个防御层都执行一套由管理员决定的安全策略。

my-assignmentexpert™ 网络安全network security作业代写，免费提交作业要求， 满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕 博写手团队，所有订单可靠准时，保证 100% 原创。my-assignmentexpert™， 最高质量的网络安全network security作业代写，服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。 由于统计Statistics作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此网络安全network security作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的网络安全network security代写服务。我们的专家在数学Mathematics代写方面经验极为丰富，各种网络安全network security相关的作业也就用不着 说。

我们提供的网络安全network security及其相关学科的代写，服务范围广, 其中包括但不限于:

非线性方法 nonlinear method functional analysis

变分法 Calculus of Variations

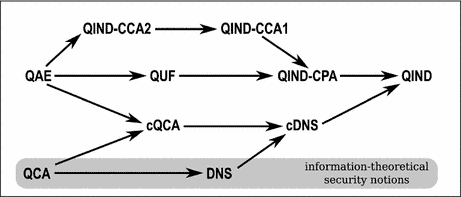
数学代写|网络安全作业代写network security代考|Security for Multiple Encryptions

Definition $3.8$ deals with the case where the communicating parties transmit a single ciphertext that is observed by an eavesdropper. It would be convenient, however, if the communicating parties could securely send multiple ciphertexts to each other-all generated using the same key-even if an eavesdropper might observe all of them. For such applications we need an encryption scheme secure for the encryption of multiple messages.

We begin with an appropriate definition of security for this setting. As in the case of Definition 3.8, we first introduce an appropriate experiment defined for any encryption scheme $\Pi$, adversary $\mathcal{A}$, and security parameter $n$ :
The multiple-message eavesdropping experiment $\operatorname{PrivK}_{\mathcal{A}, \Pi}^{\mathrm{mult}}(n)$ :

1. The adversary $\mathcal{A}$ is given input $1^{n}$, and outputs a pair of equal-length lists of messages $\vec{M}{0}=\left(m{0,1}, \ldots, m_{0, t}\right)$ and $\vec{M}{1}=$ $\left(m{1,1}, \ldots, m_{1, t}\right)$, with $\left|m_{0, i}\right|=\left|m_{1, i}\right|$ for all $i$.
2. A key $k$ is generated by running $\operatorname{Gen}\left(1^{n}\right)$, and a uniform bit $b \in{0,1}$ is chosen. For all $i$, the ciphertext $c_{i} \leftarrow$ Enc $_{k}\left(m_{b, i}\right)$ is computed and the list $\vec{C}=\left(c_{1}, \ldots, c_{t}\right)$ is given to $\mathcal{A}$.
3. $\mathcal{A}$ outputs a bit $b^{\prime}$.
4. The output of the experiment is defined to be 1 if $b^{\prime}=b$, and 0 otherwise.
   The definition of security is the same as before, except that it now refers to the above experiment.

数学代写|网络安全作业代写network security代考|Chosen-Plaintext Attacks and CPA-Security

Chosen-plaintext attacks capture the ability of an adversary to exercise (partial) control over what the honest parties encrypt. Imagine a scenario in which two honest parties share a key $k$, and the attacker can influence those parties to encrypt messages $m_{1}, m_{2}, \ldots$ (using $k$ ) and send the resulting ciphertexts over a channel that the attacker can observe. At some later point in time, the attacker observes a ciphertext corresponding to some unknown message $m$ encrypted using the same key $k$; let us even assume that the attacker knows that $m$ is one of two possibilities $m_{0}, m_{1}$. Security against chosen-plaintext attacks means that even in this case the attacker cannot tell which of those two messages was encrypted with probability significantly better than random guessing. (For now we revert back to the case where the eavesdropper is given only a single encryption of an unknown message. Shortly, we will return to consideration of the multiple-message case.)

数学代写|网络安全作业代写NETWORK SECURITY代考|CPA-Security for Multiple Encryptions

Definition $3.21$ can be extended to the case of multiple encryptions in the same way that Definition $3.8$ is extended to give Definition 3.18, i.e., by using lists of plaintexts. Here, we take a different approach that is somewhat simpler and has the advantage of modeling attackers that can adaptively choose pairs of plaintexts to be encrypted. Specifically, we now give the attacker access to a “left-or-right” oracle $\mathrm{LR}{k, b}$ that, on input a pair of equal-length messages $m{0}, m_{1}$, computes the ciphertext $c \leftarrow$ Enc $_{k}\left(m_{b}\right)$ and returns $c$. That is, if $b=0$ then the adversary always receives an encryption of the “left” plaintext, and if $b=1$ then it always receives an encryption of the “right” plaintext. The bit $b$ is a uniform bit chosen at the beginning of the experiment, and as in previous definitions the goal of the attacker is to guess $b$.

Consider the following experiment defined for any encryption scheme $\Pi=$ (Gen, Enc, Dec), adversary $\mathcal{A}$, and value $n$ for the security parameter:
The LR-oracle experiment PrivK ${ }_{\mathcal{A}, \Pi}^{\mathrm{LR}-\mathrm{cpa}}(n)$ :

1. A key $k$ is generated by running $\operatorname{Gen}\left(1^{n}\right)$.
2. A uniform bit $b \in{0,1}$ is chosen.
3. The adversary $\mathcal{A}$ is given input $1^{n}$ and oracle access to $\operatorname{LR}_{k, b}(\cdot, \cdot)$, as defined above.
4. The adversary $\mathcal{A}$ outputs a bit $b^{\prime}$.
5. The output of the experiment is defined to be 1 if $b^{\prime}=b$, and 0 otherwise. In the former case, we say that $\mathcal{A}$ succeeds.

网络安全作业代写

数学代写|网络安全作业代写NETWORK SECURITY代考|SECURITY FOR MULTIPLE ENCRYPTIONS

定义3.8处理通信方传输被窃听者观察到的单个密文的情况。然而，如果通信双方可以安全地向彼此发送多个密文——所有密文都是使用相同的密钥生成的——即使窃听者可能会观察到所有密文，这将是很方便的。对于此类应用程序，我们需要一种安全的加密方案来加密多条消息。

我们从对此设置的安全性的适当定义开始。与定义 3.8 的情况一样，我们首先引入为任何加密方案定义的适当实验圆周率, 对手一种, 和安全参数n:
多消息窃听实验隐私一种,圆周率米在l吨⁡(n) :

1. 对手一种给定输入1n, 并输出一对等长的消息列表 $\vec{M} {0}=\left(m {0,1}, \ldots, m_{0, t}\right)一种nd\ vec {M} {1} =\left(m {1,1}, \ldots, m_{1, t}\right),在一世吨H\left|m_{0, i}\right|=\left|m_{1, i}\right|F这r一种ll我$。
2. 关键ķ是通过运行生成的Gen⁡(1n), 和一个统一的位b∈0,1被选中。对全部一世, 密文C一世←编码ķ(米b,一世)计算和列表C→=(C1,…,C吨)给予一种.
3. 一种输出一点b′.
4. 实验的输出定义为 1，如果b′=b, 否则为 0。
   安全性的定义和以前一样，只是现在参考了上面的实验。

数学代写|网络安全作业代写NETWORK SECURITY代考|CHOSEN-PLAINTEXT ATTACKS AND CPA-SECURITY

选择明文攻击捕获对手行使的能力p一种r吨一世一种l控制诚实方加密的内容。想象一个场景，两个诚实的方共享一个密钥ķ，并且攻击者可以影响那些参与方加密消息$k$, and the attacker can influence those parties to encrypt messages $m_{1}, m_{2}, \ldots$ (using $k$ ) and send the resulting ciphertexts over a channel that the attacker can observe. At some later point in time, the attacker observes a ciphertext corresponding to some unknown message $m$ encrypted using the same key $k$; let us even assume that the attacker knows that $m$ is one of two possibilities $m_{0}, m_{1}$. Security against chosen-plaintext attacks means that even in this case the attacker cannot tell which of those two messages was encrypted with probability significantly better than random guessing. (For now we revert back to the case where the eavesdropper is given only a single encryption of an unknown message. Shortly, we will return to consideration of the multiple-message case.)

数学代写|网络安全作业代写NETWORK SECURITY代考|CPA-SECURITY FOR MULTIPLE ENCRYPTIONS

定义3.21可以以与定义相同的方式扩展到多重加密的情况3.8扩展为给出定义 3.18，即，通过使用明文列表。在这里，我们采用了一种不同的方法，该方法更简单，并且具有对攻击者进行建模的优势，可以自适应地选择要加密的明文对。具体来说，我们现在让攻击者访问“左或右”预言机oracle $\mathrm{LR}{k, b}$ that, on input a pair of equal-length messages $m{0}, m_{1}$, computes the ciphertext $c \leftarrow$ Enc $_{k}\left(m_{b}\right)$ and returns $c$. That is, if $b=0$ then the adversary always receives an encryption of the “left” plaintext, and if $b=1$ then it always receives an encryption of the “right” plaintext. The bit $b$ is a uniform bit chosen at the beginning of the experiment, and as in previous definitions the goal of the attacker is to guess $b$.

考虑为任何加密方案定义的以下实验圆周率$\Pi=$ (Gen, Enc, Dec), adversary $\mathcal{A}$, and value $n$ for the security parameter:
The LR-oracle experiment PrivK ${ }_{\mathcal{A}, \Pi}^{\mathrm{LR}-\mathrm{cpa}}(n)$ :

1. 关键ķ是通过运行生成的Gen⁡(1n).
2. 一个统一的位b∈0,1被选中。
3. 对手一种给定输入1n和 oracle 访问LRķ,b⁡(⋅,⋅)，如上定义。
4. 对手一种输出一点b′.
5. 实验的输出定义为 1，如果b′=b, 否则为 0。在前一种情况下，我们说一种成功。

数学代写|网络安全作业代写network security代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。

抽象代数Galois理论代写

偏微分方程代写成功案例

代数数论代考

概率论代考

离散数学代写

集合论数理逻辑代写案例

时间序列分析代写

离散数学网课代修