数学代写| Quadratic Equations 离散代考 离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形…
离散数学
数学代写| Quadratic Equations 离散代考 离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形…
数学代写| Undirected Graphs 代考 离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形式方法,…
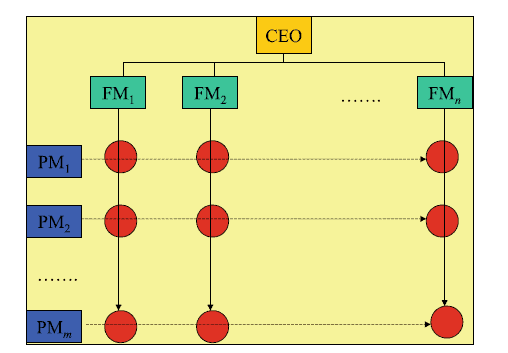
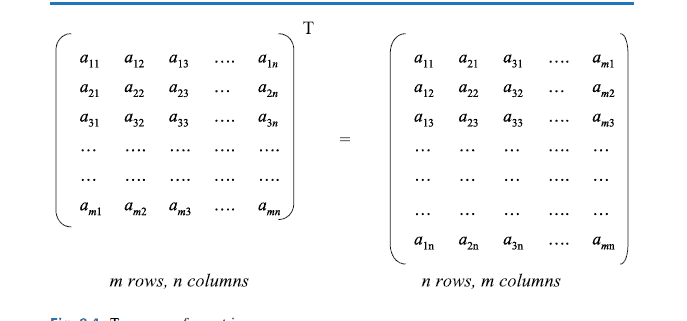
There are many applications of matrices in business and economics, and the field of linear programming often involves solving systems of linear equations. The organization structure of many organizations today is matrix orientated rather than the traditional functional structure with single managerial responsibility for a functional area in the organization. A matrix organization is one in which there is dual or multiple managerial accountability and responsibility, and there are generally two chains of command, with the first being along traditional functional lines and the second being along project or client Fig. 8.6.
That is, each person in a matrix organization is essentially reporting to two managers: their line manager for the functional area that they work in, and the project manager for the project that they are assigned to. The project is a temporary activity and so this reporting line ceases on project closure, whereas the functional line is more permanent (subject to the regular changes following company reorganizations as part of continuous improvement).
Another application of matrices in business is that of a decision matrix that allows an organization to make decisions objectively based on criteria. For example, the tool evaluation matrix in Table $8.1$ lists all of the requirements vertically that the tool is to satisfy, and the candidate tools that are to be evaluated and rated against each requirement are listed horizontally. Various rating schemes may be employed, and a simple numeric mechanism is employed in the example. The tool evaluation criteria are used to rate the effectiveness of each candidate tool, and
8.7 Business Applications of Matrices
145
\begin{tabular}{|l|l|l|l|l|l|l|}
\hline Table 8.1 Tool evaluation & & Tool 1 & Tool 2 & $\ldots$ & Tool $k$ \
\hline matrix & Requirement 1 & 8 & 7 & 9 \
\hline Requirement 2 & 4 & 6 & 8 \
\hline$\ldots$ & $\ldots$ & & & \
\hline & Requirement $n$ & 3 & 6 & & 8 \
\hline Total & 35 & 38 & $\ldots$ & 45 \
\hline
\end{tabular}
indicate the extent to which the tool satisfies the defined requirements. The chosen tool in this example is Tool $k$ as it is the most highly rated of the evaluated tools.
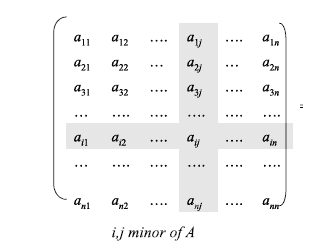
There are many applications of matrices in the computing field including in cryptography, coding theory and graph theory. For more detailed information on matrix theory see [2].、
数学代写| Gaussian Elimination 代考 离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形式…
数学代写| Matrix Operations 代考 离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形式方法,…
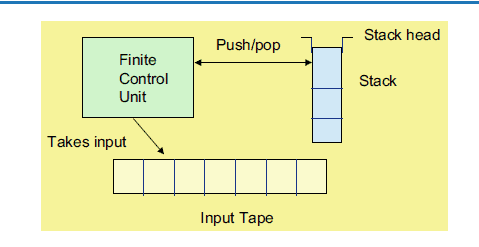
数学代写| Pushdown Automata 离散代考 离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形式方…