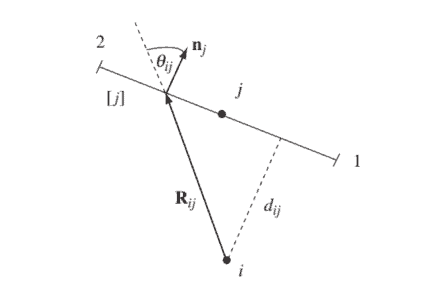
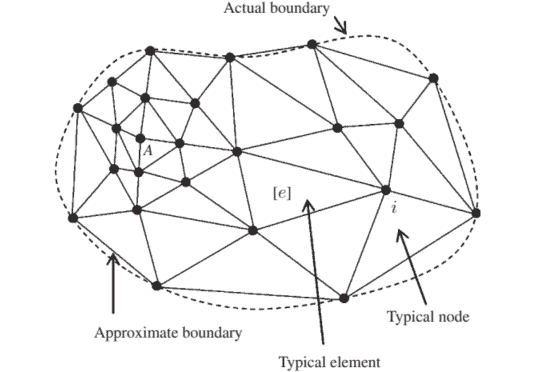
如果你也在 怎样代写有限元方法finite differences method这个学科遇到相关的难题,请随时右上角联系…
CS555
Numerical Methods for Partial Differential Equations (CS 555) Spring 2022
| What | Where |
|---|---|
| Time/place | Wed/Fri 11:00am-12:15pm 3025 Campuse Instructional Facility/ Catalog |
| Class URL | https://bit.ly/numpde-s22 |
| Live lecture | Participate » · Send instant message |
| Class recordings | Watch » |
| Forum | Discuss » (needs user account) |
| Calendar | View » |
| Office Hours | Participate » (Please use Chrome/Chromium to connect for now) |
Homework
- Homework 1 (due Feb 11)
- Homework 2 (due Feb 25)
Quizzes and Feedback Form
- Quiz 1 (Feb 9)
Project
(none yet)Why you should take this class
This course covers the basics of finite difference schemes, finite volume schemes, and finite element methods. In addition, we'll cover some advanced topics such as discontinuous Galerkin and integral equation methods, time permitting. One of the goals of this course is to build intuition for these methods. We will be providing background for many of the computational and mathematical concepts in the course. As such, you do not need to be an expert in PDEs or in coding. But you should have a course in numerical analysis as your background (CS450 or equivalent), be comfortable with differential equations, and have some coding experience. The course is divided in roughly two parts: hyperbolic and elliptic. This is of course a generalization, but it does allow us to focus on finite difference/finite volume methods for one part of the course and finite elements for another part. In addition to model problems we'll look at Stokes and other equations in order to develop a full understanding of the methods. The course involves several homeworks (usually bi-weekly) and two projects: a midsemester project and a final project. There is also a participation grade based on quizzes. The course homeworks and examples in class will be in Python. In particular, we'll use numpy and scipy.Instructor

Course Outline
Note: the section headings in this tree are clickable to reveal more detail.- Introduction
- Notes
- Notes (unfilled, with empty boxes)
- About the Class
- Classifcation of PDEs
- Preliminaries: Differencing
- Interpolation Error Estimates (reference)
- Demo: Elliptic PDE Illustrating the Maximum Principle
- Demo: Elliptic PDE Radially Symmetric Singular Solution
- Demo: Finite Differences vs Noise
- Demo: Finite Differences
- Demo: Floating point vs Finite Differences
- Demo: Hyperbolic PDE
- Demo: Interpolation Error
- Demo: Parabolic PDE
- Demo: Taking Derivatives with Vandermonde Matrices
- Finite Difference Methods for Time-Dependent Problems
- Finite Volume Methods for Hyperbolic Conservation Laws
- Finite Element Methods for Elliptic Problems
- tl;dr: Functional Analysis
- Back to Elliptic PDEs
- Galerkin Approximation
- Finite Elements: A 1D Cartoon
- Finite Elements in 2D
- Approximation Theory in Sobolev Spaces
- Saddle Point Problems, Stokes, and Mixed FEM
- Non-symmetric Bilinear Forms
- Demo: 2D FEM Using Firedrake
- Demo: 2D Stokes Using Firedrake
- Demo: Bad Discretizations for 2D Stokes
- Demo: Developing FEM in 1D
- Demo: Developing FEM in 2D
- Demo: Rates of Convergence
- Discontinuous Galerkin Methods for Hyperbolic Problems
Computing
We will be using Python with the libraries numpy, scipy and matplotlib for assignments. No other languages are permitted. Python has a very gentle learning curve, so you should feel at home even if you've never done any work in Python.Books and Source Material
Draft Textbook
Once you sign in and complete your enrollment in RELATE, you will gain access to a draft textbook that was made available by Luke Olson.Supplementary Text Books

Strikwerda, John C. Finite Difference Schemes and Partial Differential Equations. (available as an e-book via the UIUC library) Society for Industrial and Applied Mathematics, 2004. Second edition. DOI.

LeVeque, Randall J. Numerical Methods for Conservation Laws. (available as an e-book via the UIUC library) 2nd ed. Birkhäuser Basel, 1992. DOI.

Braess, Dietrich. Finite Elements: Theory, Fast Solvers, and Applications in Solid Mechanics. (available as an e-book via the UIUC library) Cambridge University Press, 2007. DOI.
Previous editions of this class
Computing Resources
Firedrake
Python
- Python tutorial
- Facts and myths about Python names and values
- Dive into Python 3
- Learn Python the hard way
- Project Euler (Lots of practice problems)
Numpy
- Introduction to Python for Science
- The SciPy lectures
- The Numpy MedKit by Stéfan van der Walt
- The Numpy User Guide by Travis Oliphant
- Numpy/Scipy documentation
- More in this reddit thread
- Spyder (a Python IDE, like Matlab) is installed in the virtual machine. (Applications Menu > Development > Spyder)
- An introduction to Numpy and SciPy
- 100 Numpy exercises
Grading Policies
如果你也在 怎样代写有限元方法finite differences method这个学科遇到相关的难题,请随时右上角联系…
如果你也在 怎样代写有限元方法finite differences method这个学科遇到相关的难题,请随时右上角联系…
如果你也在 怎样代写有限元方法finite differences method这个学科遇到相关的难题,请随时右上角联系…
如果你也在 怎样代写有限元方法finite differences method这个学科遇到相关的难题,请随时右上角联系…
如果你也在 怎样代写有限元方法finite differences method这个学科遇到相关的难题,请随时右上角联系…
数学代写|Some clarification of terminology 数值分析代考 数值分析代写 When di…
数学代写|Example Polynomial approximation 数值分析代写 数值分析代写 Determin…
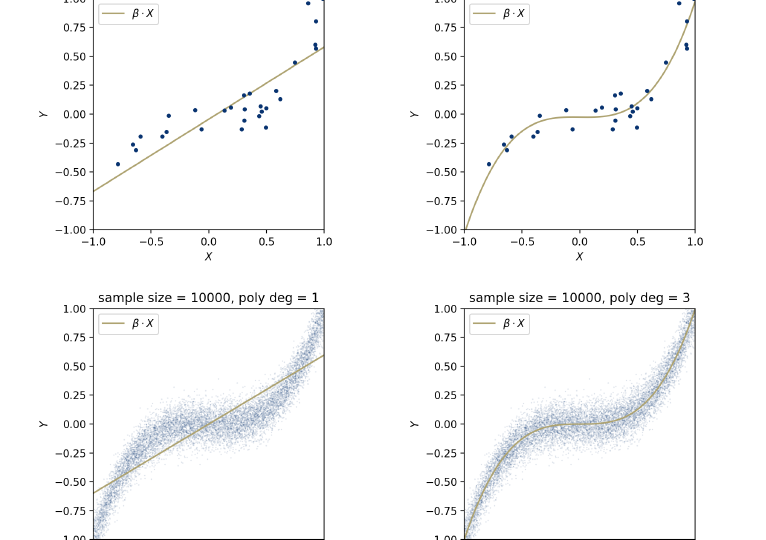
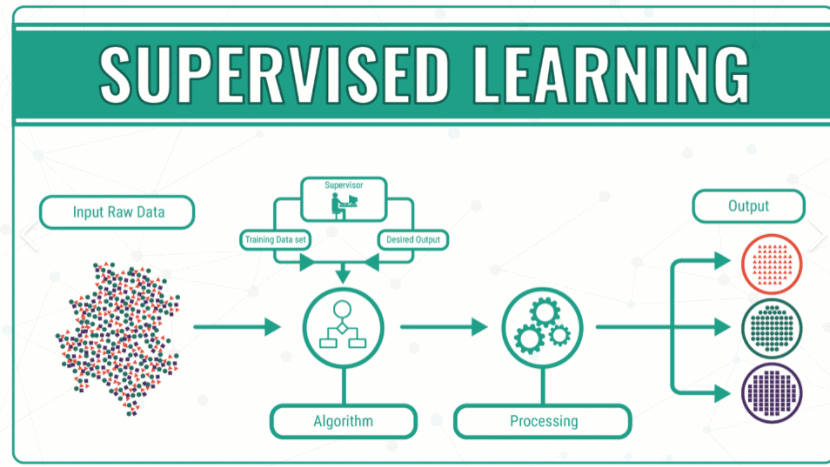
数学代写|Basic Concepts in Supervised Machine Learning 数值分析代考 数值…