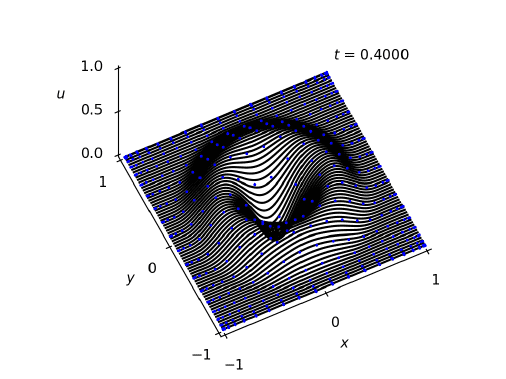
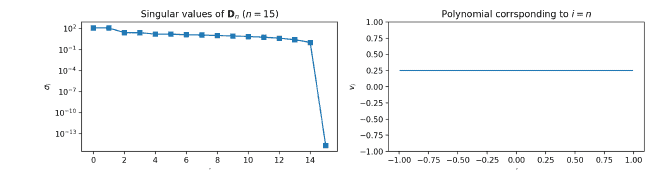
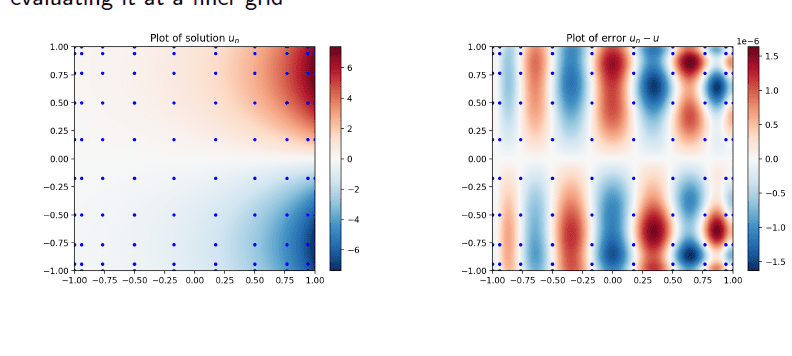
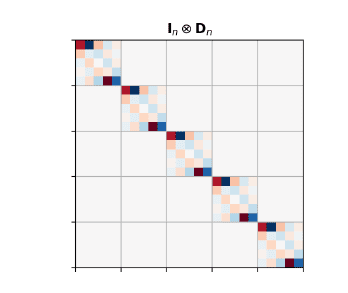
数学代写|Perturbations 数值分析代考 数值分析代写 Consider the special case, …
Math 6641
Math 6641 Advanced Numerical Methods for Partial Differential Equations Course Information (Spring 2022)
| Time: | T R 15:30-16:45 | |
| Place: | Skiles 268 | |
| Reference books: | ||
| J. W. Thomas, | Introduction to Numerical Methods for Partial Differential Equations, Springer, ISBM 0-387-97999-9. | |
| L. N. Trefethen, | Spectral Methods in Matlab, SIAM. | |
| S. C. Brenner and R. Scott, | The Mathematical Theory of Finite Element Methods, Second Edition. | |
| Claes Johnson, | Numerical solution of partial differential equations by the finite element method, Cambridge University Press, 1992. ISBN 0521 345 146 | |
| R. J. LeVeque, | Numerical Methods for Conservation Laws, Birkhauser Verlag, 1992. | |
| Vidar Thomee, | Galerkin finite element method for parabolic problems. | |
| S. V. Patankar, | Numerical Heat Transfer and Fluid Flow, Hemisphere Publishing Corp., 1980. | |
| C.-W. Shu, | Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws, in Advanced Numerical Approximation of Nonlinear Hyperbolic Equations, B. Cockburn, C. Johnson, C.-W. Shu and E. Tadmor (Editor: A. Quarteroni) , Lecture Notes in Mathematics, volume 1697, Springer, 1998, pp.325-432. | |
| Instructor: | Dr. Yingjie Liu | |
| Office: | Skiles 134 | |
| Phone: | (404)894-2381 | |
| E-mail: | [email protected] | |
| WWW: | www.math.gatech.edu/~yingjie | |
| Office Hours: | T R 16:45-17:45 | |
| Homework: | Homeworks will be assigned once every couple of weeks and they must be turned in on time. | |
| Grading: | Homework 50%, final 50%. | |
| Topics: | Some recent development in high order methods for conservation laws and related equations will be discussed, such as FCT and flux limiter, MUSCL and slope limiter, finite difference and finite volume ENO/WENO schemes on rectangular and unstructured meshes; central scheme, central scheme on overlapping cells; discontinuous Galerkin method (DG), LDG and central DG on overlapping cells; Hierarchical reconstruction methods (HR) for reducing numerical artifacts (due to non smoothness of the solution) on unstructured triangular meshes; finite volume methods with HR etc. Some classical methods for solving Navier-Stokes equation of incompressible fluids will be introduced, such as the Marker-and-Cell method, projection method, mixed finite element methods etc. Interface tracking and capturing methods will be covered, including front-tracking, volume of fluids and the level set methods. Recent development on BFECC method and its limiting for solving time dependent Hamilton-Jacobi equations on regular or irregular meshes, and BFECC for solving Maxwell's equations for electromagnetic waves and for perfectly matched layers (PML). Recent development on neural network methods for solving conservation laws. | |
| Homework 1, due Mar. 1, 2022. |
数学代写|Some clarification of terminology 数值分析代考 数值分析代写 When di…
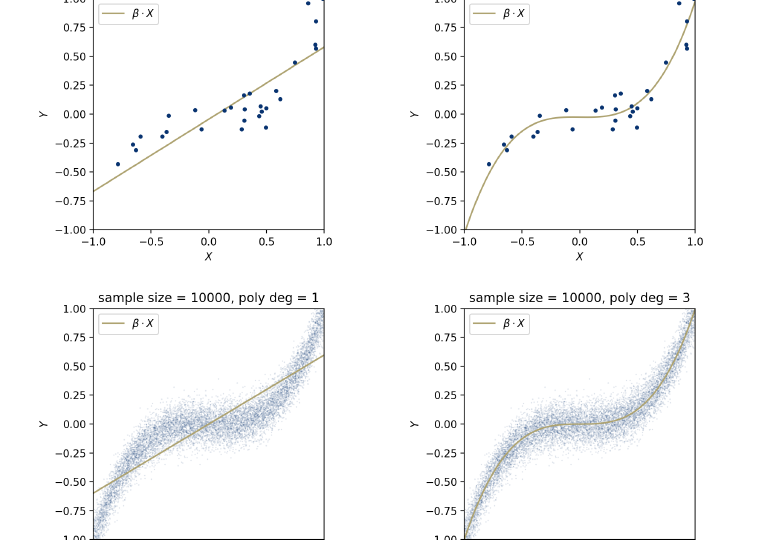
数学代写|Example Polynomial approximation 数值分析代写 数值分析代写 Determin…
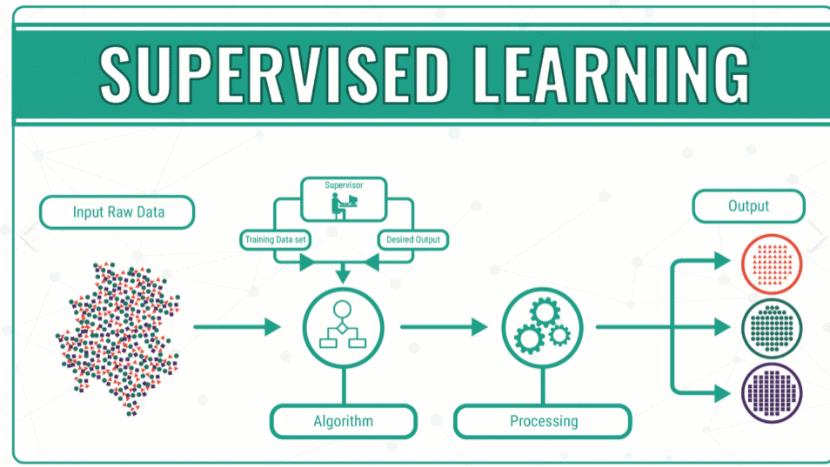
数学代写|Basic Concepts in Supervised Machine Learning 数值分析代考 数值…
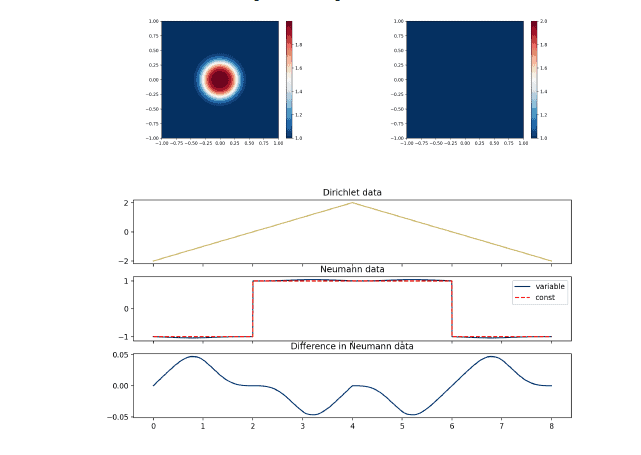
数学代写|Mean Value Property 数值分析代考 数值分析代写 Recall that solution …
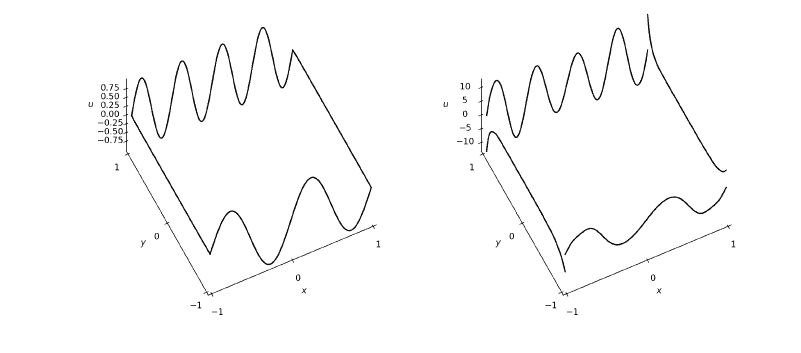
数学代写|The rank of the Chebyshev differentiation matrix数值分析代考 …
数学代写| Example Laplace’s equation 数值分析代考 数值分析代写 Let us solve …
数学代写|Differentiation in matrix form 数值分析代写 数值分析代写 The applic…
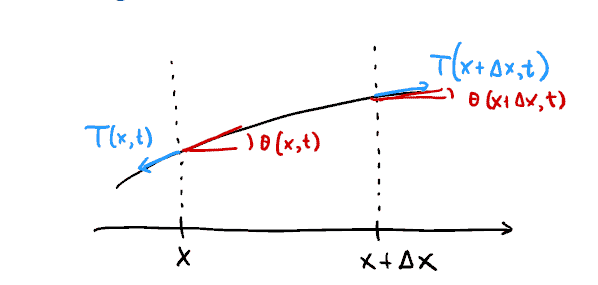
数学代写| Tightly stretched string 数值分析代考 数值分析代写 Imagine a tight…
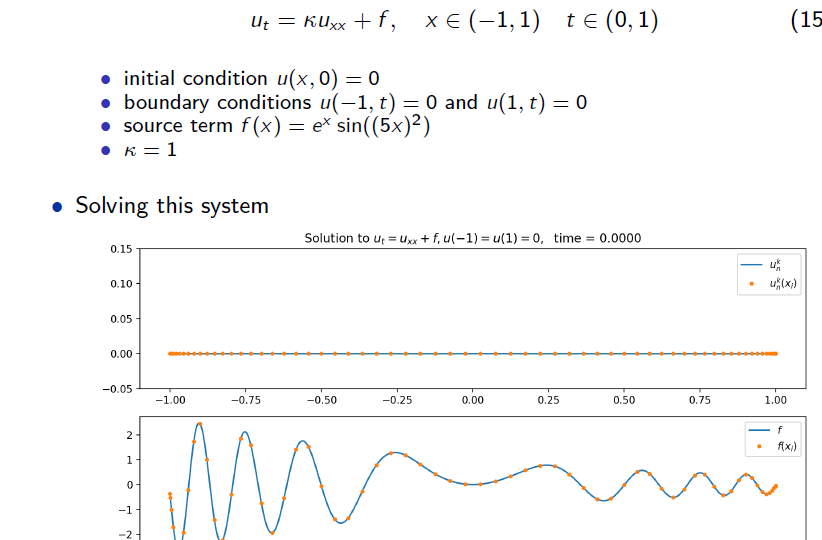
数学代写| An example of the heat equation 数值分析代考 数值分析代写 Consider…