0 0

By admin 数学代写 2022年2月23日

The extreme values theorem says continuous functions achieve their maximum and minimum provided they are defined on a sequentially compact set.
Example 6.3.1 Let $f(x)=1 / x$ for $x \in(0,1)$.
Clearly, $f$ is not bounded. Does this violate the conclusion of the above lemma? It does not because the end points of the interval involved are not in the interval. The same function defined on $[.000001,1)$ would have been bounded although in this case the boundedness of the function would not follow from the above lemma because it fails to include the right endpoint.
The next theorem is known as the max min theorem or extreme value theorem.
Theorem $6.3 .2$ Let $K \subseteq \mathbb{F}^{p}$ be sequentially compact and let $f: K \rightarrow \mathbb{R}$ be continuous. Then $f$ achieves its maximum and its minimum on $K$. This means there exist, $x_{1}, x_{2} \in K$ such that for all $x \in K, f\left(x_{1}\right) \leq f(x) \leq f\left(x_{2}\right)$.

Proof: Let $\lambda \equiv \sup {f(x): x \in K}$. Then if $l<\lambda$, there exists $x \in K$ such that $f(x)>l$ since otherwise, $\lambda$ is not as defined since $l$ would be a smaller upper bound. Thus there exists a sequence $\left{x_{n}\right} \in K$ such that $\lim {n \rightarrow \infty} f\left(x{n}\right)=\lambda$. This is called a maximizing sequence. Since $K$ is sequentially compact, there exists a subsequence $\left{x_{n_{k}}\right}$ which converges to $x \in K$. Therefore, $\lambda=\lim {k \rightarrow \infty} f\left(x{n_{k}}\right)=f(x)$ so $f$ achieves its maximum value. A similar argument using a minimizing sequence and $\eta \equiv \inf {f(x): x \in K}$ shows $f$ achieves its minimum value on $K$.

In fact a continuous function takes compact sets to compact sets. This is another of those big theorems which tends to hold whenever it makes sense. Therefore, I will be vague about the domain and range of the function $f$.
continuous, it satisfies the inverse image of open sets being open condition. For $U \in \mathcal{C}$, $$ f^{-1}(U)=O_{U} \cap D(f) \text {, where } O_{U} \text { is open } $$
103
Lemma 6.4.1 If $f$ is continuous on the closed interval $[a, b]$ and for some $x \in$ $[a, b], f(x) \neq c$, then there exists $\delta>0$ such that for $y \in[a, b] \cap(x-\delta, x+\delta)$, the sign of $f(y)-c$ is constant. That is, it is either always positive or always negative depending on the sign of $f(x)-c$.

Proof: Let $\varepsilon=|f(x)-c|>0$ by assumption. Then let $\delta$ correspond to this $\varepsilon$ in the definition of continuity.

Case 1: $f(x)-c>0$. Then for $y \in[a, b] \cap(x-\delta, x+\delta), f(x)-f(y)<f(x)-c$ and so $0<f(y)-c$.

Case 2: $f(x)-c<0 .$ Then for $y \in[a, b] \cap(x-\delta, x+\delta), f(y)-f(x)f(y)-c$.
Next here is a proof of the intermediate value theorem.
Theorem 6.4.2 Suppose $f:[a, b] \rightarrow \mathbb{R}$ is continuous and suppose $f(a)<c<$ $f(b)$. Then there exists $x \in(a, b)$ such that $f(x)=c$.
104 CHAPTER $6 .$ CONTINUOUS FUNCTIONS \begin{tabular}{l} Proof: Let $d=\frac{a+b}{2}$ and consider the intervals $[a, d]$ and $[d, b] .$ If $f(d) \geq c$, then on \ $d]$, the function is $\leq c$ at one end point and $\geq c$ at the other. On the other hand, if \ \hline$d b$ & Ond point and $\leq 0$ at the other. Pick the interval \end{tabular} $f(d) \leq c$, then on $[d, b], f \geq 0$ at one end point and $\leq 0$ at the other. Pick the interval on which $f$ has values which are at least as large as $c$ and values no larger than c. Now
that on one of these smaller intervals, the function has values at least as large as $c$ and values no larger than $c$. Continue in this way. Next apply the nested interval lemma to get $x$ in all these intervals. In the $n^{\text {th }}$ interval, let $x_{n}, y_{n}$ be points of this interval such that $f\left(x_{n}\right) \leq c, f\left(y_{n}\right) \geq c .$ Now $\left|x_{n}-x\right| \leq(b-a) 2^{-n}$ and $\left|y_{n}-x\right| \leq(b-a) 2^{-n}$ and so $x_{n} \rightarrow x$ and $y_{n} \rightarrow x$. Therefore, from Theorem $6.1 .1$ and limit theorems for sequences, Theorem 4.4.13,
$$
f(x)-c=\lim {n \rightarrow \infty}\left(f\left(x{n}\right)-c\right) \leq 0
$$
while
$$
f(x)-c=\lim {n \rightarrow \infty}\left(f\left(y{n}\right)-c\right) \geq 0 .
$$
Consequently $f(x)=c$ and this proves the theorem.
Here is another proof of this major theorem.
Proof: Since $f(a)<c$, the set, $S$ defined as
$$
S \equiv{x \in[a, b]: f(t) \leq c \text { for all } t \in[a, x]}
$$
is nonempty. In particular $a \in S$. Note that $b \notin S$ by assumption. Let $z \equiv \sup (S)$. By Lemma 6.4.1, since $f(a)<c$ it follows that $z \in(a, b)$. By the same lemma again, if $f(z) \neq c$, then $z \neq \sup (S) .$ Hence $f(z)=c .$

Lemma $6.4 .3$ Let $\phi:[a, b] \rightarrow \mathbb{R}$ be a continuous function and suppose $\phi$ is $1-1$ on $(a, b)$. Then $\phi$ is either strictly increasing or strictly decreasing on $[a, b]$.

Proof: First it is shown that $\phi$ is either strictly increasing or strictly decreasing on $(a, b)$.

If $\phi$ is not strictly decreasing on $(a, b)$, then there exists $x_{1}0 .
$$
If for some other pair of points, $x_{2}0$, there exists $t \in(0,1)$ such that $h(t)=0 .$ Therefore, both $x_{t}$ and $y_{t}$ are points of $(a, b)$ and $\phi\left(y_{t}\right)-\phi\left(x_{t}\right)=0$ contradicting the assumption that $\phi$ is one to one. It follows $\phi$ is either strictly increasing or strictly decreasing on $(a, b)$.

This property of being either strictly increasing or strictly decreasing on $(a, b)$ carries over to $[a, b]$ by the continuity of $\phi .$ Suppose $\phi$ is strictly increasing on $(a, b)$. (A similar argument holds for $\phi$ strictly decreasing on $(a, b)$.) If $x>a$, then let $z_{n}$ be a decreasing sequence of points of $(a, x)$ converging to $a$. Then by continuity of $\phi$ at $a$,
$$
\phi(a)=\lim {n \rightarrow \infty} \phi\left(z{n}\right) \leq \phi\left(z_{1}\right)<\phi(x) .
$$
105
Therefore, $\phi(a)<\phi(x)$ whenever $x \in(a, b)$.
Corollary $6.4 .4$ Let $f:(a, b) \rightarrow \mathbb{R}$ be one to one and continuous. Then $f((a, b))$ is an open interval, $(c, d)$ and $f^{-1}:(c, d) \rightarrow(a, b)$ is continuous.

Proof 1: Since $f$ is either strictly increasing or strictly decreasing, it follows that $f(a, b)$ is an open interval, $(c, d)$. Assume $f$ is decreasing. Now let $x \in(a, b)$. Why is $f^{-1}$ is continuous at $f(x)$ ? Since $f$ is decreasing, if $f(x)0$ be given. Let $\varepsilon>\eta>0$ and $(x-\eta, x+\eta) \subseteq(a, b)$. Then $f(x) \in(f(x+\eta), f(x-\eta))$. Let
$$
\delta=\min (f(x)-f(x+\eta), f(x-\eta)-f(x)) .
$$
Then if $|f(z)-f(x)|<\delta$, it follows
$$
z \equiv f^{-1}(f(z)) \in(x-\eta, x+\eta) \subseteq(x-\varepsilon, x+\varepsilon)
$$
so
$$
\left|f^{-1}(f(z))-x\right|=\left|f^{-1}(f(z))-f^{-1}(f(x))\right|<\varepsilon .
$$ This proves the theorem in the case where $f$ is strictly decreasing. The case where $f$ is increasing is similar.

Proof 2: Note that since $f$ is either strictly increasing or strictly decreasing, it maps an open interval to an open interval. Now let $U$ be an open set. Thus $U=\cup_{x \in U} I_{x}$ where $I_{x}$ is an open interval. Then
$$
\begin{aligned}
\left(f^{-1}\right)^{-1}(U) &=\left(f^{-1}\right)^{-1}\left(\cup_{x \in U} I_{x}\right)=\cup_{x \in U}\left(f^{-1}\right)^{-1}\left(I_{x}\right) \
&=\cup_{x \in U}\left(f^{-1}\right)^{-1}\left(I_{x} \cap(a, b)\right)=\cup_{x \in U} f\left(I_{x} \cap(a, b)\right)
\end{aligned}
$$
which is a union of open intervals and is therefore, open.with strict inequality holding for at least one of these inequalities since not both $t$ and $(1-t)$ can equal zero. Now define
$$
h(t) \equiv\left(\phi\left(y_{t}\right)-\phi\left(x_{t}\right)\right)\left(y_{t}-x_{t}\right) .
$$
Since $h$ is continuous and $h(0)<0$, while $h(1)>0$, there exists $t \in(0,1)$ such that $h(t)=0 .$ Therefore, both $x_{t}$ and $y_{t}$ are points of $(a, b)$ and $\phi\left(y_{t}\right)-\phi\left(x_{t}\right)=0$ contradicting the assumption that $\phi$ is one to one. It follows $\phi$ is either strictly increasing or strictly decreasing on $(a, b)$.

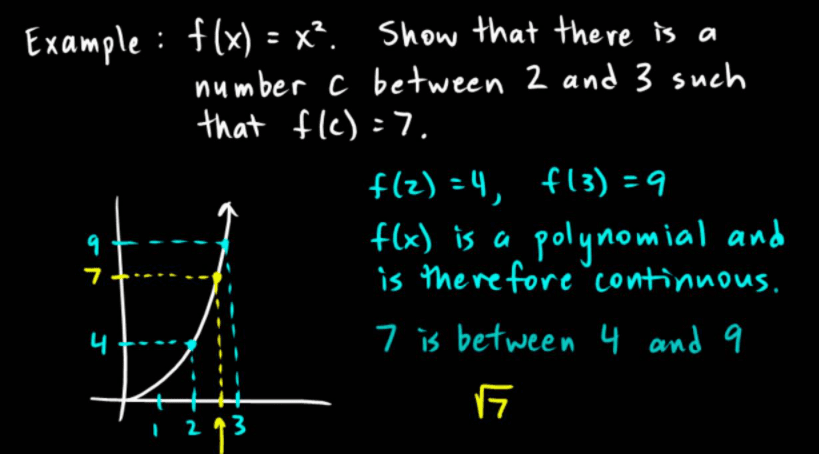
极值定理说，如果连续函数是在一个顺序紧集上定义的，它们就会达到它们的最大值和最小值。
例 6.3.1 令 $f(x)=1 / x$ 对于 $x \in(0,1)$。
显然，$f$ 是无界的。这是否违反了上述引理的结论？不是因为所涉及的区间的端点不在区间内。在 $[.000001,1)$ 上定义的相同函数将是有界的，尽管在这种情况下，函数的有界性不会从上述引理中得出，因为它没有包含正确的端点。
下一个定理被称为最大最小定理或极值定理。
定理 $6.3 .2$ 令 $K \subseteq \mathbb{F}^{p}$ 是顺序紧致的并且令 $f: K \rightarrow \mathbb{R}$ 是连续的。然后$f$ 在$K$ 上达到最大值和最小值。这意味着存在 $x_{1}, x_{2} \in K$ 使得对于所有 $x \in K, f\left(x_{1}\right) \leq f(x) \leq f\左（x_{2}\右）$。

证明：设$\lambda \equiv \sup {f(x): x \in K}$。那么如果$l<\lambda$，存在$x\in K$ 使得$f(x)>l$，否则$\lambda$ 不是定义的，因为$l$ 将是一个较小的上界。因此存在一个序列 $\left{x_{n}\right} \in K$ 使得 $\lim {n \rightarrow \infty} f\left(x{n}\right)=\lambda$ .这称为最大化序列。由于$K$ 是顺序紧致的，因此存在一个收敛到$x \in K$ 的子序列$\left{x_{n_{k}}\right}$。因此，$\lambda=\lim {k \rightarrow \infty} f\left(x{n_{k}}\right)=f(x)$ 所以$f$ 达到最大值。使用最小化序列和 $\eta \equiv \inf {f(x): x \in K}$ 的类似论证表明 $f$ 在 $K$ 上达到其最小值。

事实上，连续函数将紧集转换为紧集。这是另一个在有意义时往往成立的大定理。因此，我将对函数 $f$ 的域和范围含糊其辞。
连续，满足开集为开条件的逆象。对于 $U \in \mathcal{C}$，$$ f^{-1}(U)=O_{U} \cap D(f) \text {，其中 } O_{U} \text { 是开放的 } $$
103
引理 6.4.1 如果 $f$ 在闭区间 $[a, b]$ 上是连续的并且对于某个 $x \in$ $[a, b], f(x) \neq c$，则存在 $\ delta>0$ 使得对于 $y \in[a, b] \cap(x-\delta, x+\delta)$，$f(y)-c$ 的符号是恒定的。也就是说，它要么总是正的，要么总是负的，这取决于 $f(x)-c$ 的符号。

证明：假设 $\varepsilon=|f(x)-c|>0$。然后让$\delta$ 对应于连续性定义中的这个$\varepsilon$。

情况 1：$f(x)-c>0$。然后对于 $y \in[a, b] \cap(x-\delta, x+\delta), f(x)-f(y)<f(x)-c$ 等等 $0<f(y)- c$。

情况 2：$f(x)-c<0 .$ 那么对于 $y \in[a, b] \cap(x-\delta, x+\delta), f(y)-f(x)f(y)-c$。
接下来是中间值定理的证明。
定理 6.4.2 假设 $f:[a, b] \rightarrow \mathbb{R}$ 是连续的并且假设 $f(a)<c<$ $f(b)$。那么存在$x \in(a, b)$ 使得$f(x)=c$。
104 第 6 章 .$ 连续函数 \begin{tabular}{l} 证明：令 $d=\frac{a+b}{2}$ 并考虑区间 $[a, d]$ 和 $[d, b] .$ 如果$f(d) \geq c$，那么在\$d]$ 上，函数在一个端点是$\leq c$，在另一个端点是$\geq c$。另一方面，如果 \\hline$d b$ & Ond 点和 $\leq 0$ 在另一个。选择区间 \end{tabular} $f(d) \leq c$，然后在 $[d, b] 上，f \geq 0$ 在一个端点，$\leq 0$ 在另一个端点。选择 $f$ 的值至少与 $c$ 一样大且值不大于 c 的区间。现在
在这些较小的间隔之一上，该函数的值至少与 $c$ 一样大，并且值不大于 $c$。以这种方式继续。接下来应用嵌套间隔引理在所有这些间隔中得到 $x$。在 $n^{\text {th }}$ 区间中，设 $x_{n}, y_{n}$ 为该区间的点使得 $f\left(x_{n}\right) \leq c, f\left(y_{n}\right) \geq c .$ 现在 $\left|x_{n}-x\right| \leq(b-a) 2^{-n}$ 和 $\left|y_{n}-x\right| \leq(b-a) 2^{-n}$ 等 $x_{n} \rightarrow x$ 和 $y_{n} \rightarrow x$。因此，从定理 $6.1 .1$ 和序列的极限定理，定理 4.4.13，
$$
f(x)-c=\lim {n \rightarrow \infty}\left(f\left(x{n}\right)-c\right) \leq 0
$$
尽管
$$
f(x)-c=\lim {n \rightarrow \infty}\left(f\left(y{n}\right)-c\right) \geq 0 。
$$
因此 $f(x)=c$ 并且这证明了定理。
这是这个大定理的另一个证明。
证明：由于$f(a)<c$，集合$S$定义为
$$
S \equiv{x \in[a, b]: f(t) \leq c \text { 对于所有 } t \in[a, x]}
$$
是非空的。特别是 $a \in S$。请注意 $b \notin S$ 假设。设 $z \equiv \sup (S)$。根据引理 6.4.1，由于 $f(a)<c$，因此 $z \in(a, b)$。再次由同样的引理，如果 $f(z) \neq c$，则 $z \neq \sup (S) .$ 因此 $f(z)=c .$