0 0

By admin 数学代写 2022年2月23日

The Hausdorff maximal theorem is equivalent to the axiom of choice. Hausdorff proved it in 1914. The useful direction is what I will prove below. It will not be used much in the rest of the book which is mostly nineteenth century material. I am including it because it or something like it is either absolutely essential, as in the Hahn Banach theorem, or extremely useful to have.

Definition 3.4.1 For any set $S, \mathcal{P}(S)$ denotes the set of all subsets of $S$. It is sometimes called the power set of $S$ and is also sometimes denoted as $2^{S}$. A nonempty set $\mathcal{F}$ is called a partially ordered set if it has a partial order denoted by $\prec$. This means it satisfies the following. If $x \prec y$ and $y \prec z$, then $x \prec z$. Also $x \prec x$. It is like $\subseteq$ on the set of all subsets of a given set. It is not the case that given two elements of $\mathcal{F}$ that they are related. In other words, you cannot conclude that either $x \prec y$ or $y \prec x$. A chain, denoted by $\mathcal{C} \subseteq \mathcal{F}$ has the property that it is totally ordered meaning that if $x, y \in \mathcal{C}$, either $x \prec y$ or $y \prec x$. A maximal chain is a chain $\mathcal{C}$ which has the property that there is no strictly larger chain. In other words, if $x \in \mathcal{F} \backslash \cup \mathcal{C}$, then $\mathcal{C} \cup{x}$ is no longer a chain so $x$ fails to be related to something in $\mathcal{C}$.

Here is the Hausdorff maximal theorem. The proof is a proof by contradiction. We assume there is no maximal chain and then show that this cannot happen. The axiom of choice is used in choosing the $x_{\mathcal{C}}$ right at the beginning of the argument. See Hewitt and Stromberg $[16]$ for more of this kind of thing.

Theorem 3.4.2 Let $\mathcal{F}$ be a nonempty partially ordered set with order $\prec$. Then there exists a maximal chain.

Proof: Suppose no chain is maximal. Then for each chain $\mathcal{C}$ there exists $x_{\mathcal{C}} \in \mathcal{F} \backslash \cup \mathcal{C}$ such that $\mathcal{C} \cup\left{x_{\mathcal{C}}\right}$ is a chain. Call two chains comparable if one is a subset of the other. Let $\mathcal{X}$ be the set of all chains. Thus the elements of $\mathcal{X}$ are chains and $\mathcal{X}$ is a subset of $\mathcal{P}(\mathcal{F})$. For $\mathcal{C}$ a chain, let $\theta \mathcal{C}$ denote $\mathcal{C} \cup\left{x_{\mathcal{C}}\right}$. Pick $x_{0} \in \mathcal{F}$. A subset $\mathcal{Y}$ of $\mathcal{X}$ will be called a “tower” if $\theta \mathcal{C} \in \mathcal{Y}$ whenever $\mathcal{C} \in \mathcal{Y}, x_{0} \in \cup \mathcal{C}$ for all $\mathcal{C} \in \mathcal{Y}$, and if $\mathcal{S}$ is a subset of $\mathcal{Y}$ such that all pairs of chains in $\mathcal{S}$ are comparable, then $\cup \mathcal{S}$ is in $\mathcal{Y}$. Note that $\mathcal{X}$ is a tower. Let $\mathcal{Y}{0}$ be the intersection of all towers. Then $\mathcal{Y}{0}$ is also a tower, the smallest one. This follows from the definition.

Claim 1: If $\mathcal{C}{0} \in \mathcal{Y}{0}$ is comparable to every chain $\mathcal{C} \in \mathcal{Y}{0}$, then if $\mathcal{C}{0} \subsetneq \mathcal{C}$, it must be the case that $\theta \mathcal{C}_{0} \subseteq \mathcal{C}$. The symbol $\subsetneq$ indicates proper subset.

Proof of Claim 1: Consider $\mathcal{B} \equiv\left{\mathcal{D} \in \mathcal{Y}{0}: \mathcal{D} \subseteq \mathcal{C}{0}\right.$ or $\left.x_{\mathcal{C}{0}} \in \cup \mathcal{D}\right} .$ Let $\mathcal{Y}{1} \equiv \mathcal{Y}{0} \cap \mathcal{B}$ I want to argue that $\mathcal{Y}{1}$ is a tower. Obviously all chains of $\mathcal{Y}{1}$ contain $x{0}$ in their unions. If $\mathcal{D} \in \mathcal{Y}{1}$, is $\theta \mathcal{D} \in \mathcal{Y}{1}$ ?
case 1: $\mathcal{D} \nsupseteq \mathcal{C}{0}$. Then $x{\mathcal{C}{0}} \in \cup \mathcal{D}$ and so $x{\mathcal{C}{0}} \in \cup \theta \mathcal{D}$ so $\theta \mathcal{D} \in \mathcal{Y}{1}$.
case $2: \mathcal{D} \subseteq \mathcal{C}{0}$. Then if $\theta \mathcal{D} \nsupseteq \mathcal{C}{0}$, it follows that $\mathcal{D} \subseteq \mathcal{C}{0} \varsubsetneqq \mathcal{D} \cup\left{x{\mathcal{D}}\right} .$ If $x \in \mathcal{C}{0} \backslash \mathcal{D}$ then $x=x{\mathcal{D}}$. But then
$$
\mathcal{C}{0} \varsubsetneqq \mathcal{D} \cup\left{x{\mathcal{D}}\right} \subseteq \mathcal{C}{0} \cup\left{x{\mathcal{D}}\right}=\mathcal{C}{0} $$ which is nonsense, and so $\mathcal{C}{0}=\mathcal{D}$ so $x_{\mathcal{D}}=x_{\mathcal{C}{0}} \in \cup \theta \mathcal{C}{0}=\cup \theta \mathcal{D}$ and so $\theta \mathcal{D} \in \mathcal{Y}{1}$. If $\theta \mathcal{D} \subseteq \mathcal{C}{0}$ then right away $\theta \mathcal{D} \in \mathcal{B}$. Thus $\mathcal{B}=\mathcal{Y}{0}$ because $\mathcal{Y}{1}$ cannot be smaller than $\mathcal{Y}{0}$. In particular, if $\mathcal{D} \nsupseteq \mathcal{C}{0}$, then $x_{\mathcal{C}{0}} \in \cup \mathcal{D}$ or in other words, $\theta \mathcal{C}{0} \subseteq \mathcal{D}$.
Claim 2: Any two chains in $\mathcal{Y}{0}$ are comparable so if $\mathcal{C} \subsetneq \mathcal{D}$, then $\theta \mathcal{C} \subseteq \mathcal{D}$. Proof of Claim 2: Let $\mathcal{Y}{1}$ consist of all chains of $\mathcal{Y}{0}$ which are comparable to every chain of $\mathcal{Y}{0}$. (Like $\mathcal{C}{0}$ above.) I want to show that $\mathcal{Y}{1}$ is a tower. Let $\mathcal{C} \in \mathcal{Y}{1}$ and $\mathcal{D} \in \mathcal{Y}{0}$. Since $\mathcal{C}$ is comparable to all chains in $\mathcal{Y}{0}$, either $\mathcal{C} \subsetneq \mathcal{D}$ or $\mathcal{C} \supseteq \mathcal{D}$. I need to show that $\theta \mathcal{C}$ is comparable with $\mathcal{D}$. The second case is obvious so consider the first that $\mathcal{C} \subsetneq \mathcal{D}$. By Claim $1, \theta \mathcal{C} \subseteq \mathcal{D}$. Since $\mathcal{D}$ is arbitrary, this shows that $\mathcal{Y}{1}$ is a tower. Hence $\mathcal{Y}{1}=\mathcal{Y}{0}$ because $\mathcal{Y}{0}$ is as small as possible. It follows that every two chains in $\mathcal{Y}{0}$ are comparable and so if $\mathcal{C} \subsetneq \mathcal{D}$, then $\theta \mathcal{C} \subseteq \mathcal{D}$.

Since every pair of chains in $\mathcal{Y}{0}$ are comparable and $\mathcal{Y}{0}$ is a tower, it follows that $\cup \mathcal{Y}{0} \in \mathcal{Y}{0}$ so $\cup \mathcal{Y}{0}$ is a chain. However, $\theta \cup \mathcal{Y}{0}$ is a chain which properly contains $\cup \mathcal{Y}{0}$ and since $\mathcal{Y}{0}$ is a tower, $\theta \cup \mathcal{Y}{0} \in \mathcal{Y}{0}$. Thus $\cup\left(\theta \cup \mathcal{Y}{0}\right) \supseteq \cup\left(\cup \mathcal{Y}{0}\right) \supseteq \cup\left(\theta \cup \mathcal{Y}{0}\right)$ which is a contradiction. Therefore, it is impossible to obtain the $x{C}$ described above for some chain $\mathcal{C}$ and so, this $\mathcal{C}$ is a maximal chain.

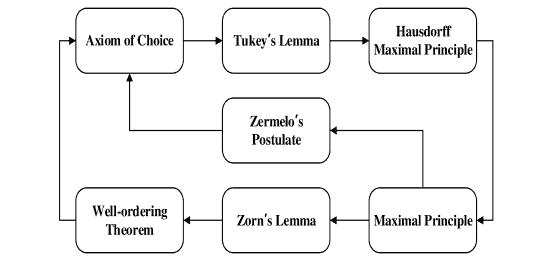
豪斯多夫最大定理等价于选择公理。 Hausdorff 在 1914 年证明了这一点。有用的方向是我将在下面证明的内容。在本书的其余部分（主要是 19 世纪的材料）中，它不会被大量使用。我包含它是因为它或类似的东西要么是绝对必要的，就像在 Hahn Banach 定理中一样，要么非常有用。

定义 3.4.1 对于任何集合 $S，\mathcal{P}(S)$ 表示 $S$ 的所有子集的集合。它有时称为 $S$ 的幂集，有时也表示为 $2^{S}$。如果一个非空集 $\mathcal{F}$ 有一个由 $\prec$ 表示的偏序，则它被称为偏序集。这意味着它满足以下条件。如果$x \prec y$ 和$y \prec z$，那么$x \prec z$。还有$x \prec x$。它就像给定集合的所有子集的集合上的 $\subseteq$。给定 $\mathcal{F}$ 的两个元素，它们并不是相关的。换句话说，你不能断定 $x \prec y$ 或 $y \prec x$。用 $\mathcal{C} \subseteq \mathcal{F}$ 表示的链具有完全有序的性质，这意味着如果 $x, y \in \mathcal{C}$，或者 $x \prec y$或 $y \prec x$。最大链是一条链$\mathcal{C}$，它具有不存在严格更大的链的性质。换句话说，如果 $x \in \mathcal{F} \backslash \cup \mathcal{C}$，那么 $\mathcal{C} \cup{x}$ 不再是链，所以 $x$ 失败与 $\mathcal{C}$ 中的某些东西相关。

这是豪斯多夫最大定理。证明是矛盾的证明。我们假设没有最大链，然后证明这不可能发生。选择公理用于选择参数开头的 $x_{\mathcal{C}}$。有关更多此类内容，请参阅 Hewitt 和 Stromberg $[16]$。

定理 3.4.2 令 $\mathcal{F}$ 是一个阶为 $\prec$ 的非空偏序集。则存在一条最大链。

证明：假设没有链是最大的。那么对于每个链 $\mathcal{C}$ 存在 $x_{\mathcal{C}} \in \mathcal{F} \backslash \cup \mathcal{C}$ 使得 $\mathcal{C} \cup\ left{x_{\mathcal{C}}\right}$ 是一个链。如果一个是另一个的子集，则称两个链具有可比性。令 $\mathcal{X}$ 为所有链的集合。因此 $\mathcal{X}$ 的元素是链，$\mathcal{X}$ 是 $\mathcal{P}(\mathcal{F})$ 的子集。对于 $\mathcal{C}$ 链，令 $\theta \mathcal{C}$ 表示 $\mathcal{C} \cup\left{x_{\mathcal{C}}\right}$。选择 $x_{0} \in \mathcal{F}$。 $\mathcal{X}$ 的子集 $\mathcal{Y}$ 将被称为“塔”，如果 $\theta \mathcal{C} \in \mathcal{Y}$ 每当 $\mathcal{C} \in \mathcal{Y}, x_{0} \in \cup \mathcal{C}$ 对于所有 $\mathcal{C} \in \mathcal{Y}$，如果 $\mathcal{S}$ 是$\mathcal{Y}$ 使得 $\mathcal{S}$ 中的所有链对都是可比较的，则 $\cup \mathcal{S}$ 在 $\mathcal{Y}$ 中。注意 $\mathcal{X}$ 是一个塔。让 $\mathcal{Y}{0}$ 成为所有塔的交集。那么 $\mathcal{Y}{0}$ 也是一座塔，最小的一座。这是从定义中得出的。

主张 1：如果 $\mathcal{C}{0} \in \mathcal{Y}{0}$ 与每条链 $\mathcal{C} \in \mathcal{Y}{0}$ 相当，那么如果$\mathcal{C}{0} \subsetneq \mathcal{C}$，它一定是$\theta \mathcal{C}_{0} \subseteq \mathcal{C}$。符号 $\subsetneq$ 表示真子集。

索赔证明 1：考虑 $\mathcal{B} \equiv\left{\mathcal{D} \in \mathcal{Y}{0}： \mathcal{D} \subseteq \mathcal{C}{0 }\right.$ 或 $\left.x_{\mathcal{C}{0}} \in \cup \mathcal{D}\right} .$ 让 $\mathcal{Y}{1} \equiv \mathcal{Y}{0} \cap \mathcal{B}$ 我想说 $\mathcal{Y}{1}$ 是一座塔。显然 $\mathcal{Y}{1}$ 的所有链在它们的联合中都包含 $x{0}$。如果 $\mathcal{D} \in \mathcal{Y}{1}$，是 $\theta \mathcal{D} \in \mathcal{Y}{1}$ 吗？
案例 1：$\mathcal{D} \nsupseteq \mathcal{C}{0}$。然后 $x{\mathcal{C}{0}} \in \cup \mathcal{D}$ 等 $x{\mathcal{C}{0}} \in \cup \theta \mathcal{D} $ 所以 $\theta \mathcal{D} \in \mathcal{Y}{1}$。
案例 $2: \mathcal{D} \subseteq \mathcal{C}{0}$。那么如果 $\theta \mathcal{D} \nsupseteq \mathcal{C}{0}$，那么 $\mathcal{D} \subseteq \mathcal{C}{0} \varsubsetneqq \mathcal{D} \cup\left{x{\mathcal{D}}\right} .$ 如果 $x \in \mathcal{C}{0} \backslash \mathcal{D}$ 那么 $x=x{\mathcal {D}}$。但是之后
$$
\mathcal{C}{0} \varsubsetneqq \mathcal{D} \cup\left{x{\mathcal{D}}\right} \subseteq \mathcal{C}{0} \cup\left\ {x{\mathcal{D}}\right}=\mathcal{C}{0} $$ 这是胡说八道，所以 $\mathcal{C}{0}=\mathcal{D}$ 所以 $x_{\mathcal{D}}=x_{\mathcal{C}{0}} \in \cup \theta \mathcal{C}{0}=\cup \theta \mathcal{D}$ 等 $\theta \mathcal{D} \in \mathcal{Y}{1}$。如果 $\theta \mathcal{D} \subseteq \mathcal{C}{0}$ 那么马上 $\theta \mathcal{D} \in \mathcal{B}$。因此 $\mathcal{B}=\mathcal{Y}{0}$ 因为 $\mathcal{Y}{1}$ 不能小于 $\mathcal{Y}{0}$。特别是，如果 $\mathcal{D} \nsupseteq \mathcal{C}{0}$，则 $x_{\mathcal{C}_{0}} \in \cup \mathcal{D}$ 或其他的话