微积分note Cauchy Sequences

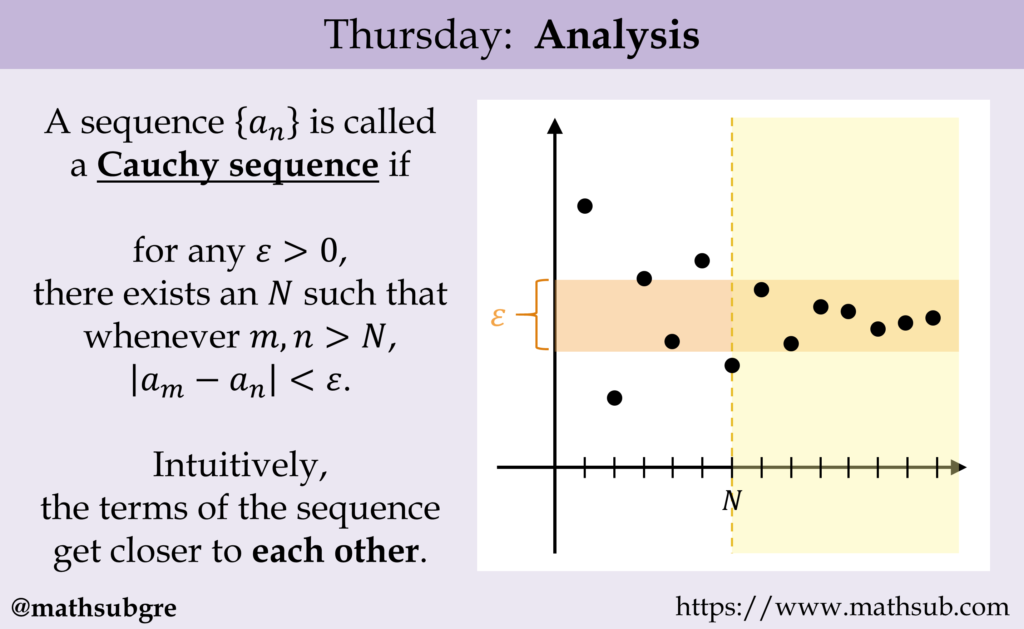
A Cauchy sequence is one which “bunches up”. This concept was developed by Bolzano and Cauchy. It is a fundamental idea in analysis.

Definition 4.5.1 $\left{a_{n}\right}$ is a Cauchy sequence if for all $\varepsilon>0$, there exists $n_{\varepsilon}$ such that whenever $n, m \geq n_{\varepsilon},\left|a_{n}-a_{m}\right|<\varepsilon$.

A sequence is Cauchy means the terms are “bunching up to each other” as $m, n$ get large.

Theorem 4.5.2 The set of terms (values) of a Cauchy sequence in $\mathbb{F}^{p}$ is bounded.
Proof: Let $\varepsilon=1$ in the definition of a Cauchy sequence and let $n>n_{1}$. Then from the definition, $\left|a_{n}-a_{n_{1}}\right|<1$. It follows from the triangle inequality that for all $n>n_{1},\left|a_{n}\right|<1+\left|a_{n_{1}}\right|$. Therefore, for all $n,\left|a_{n}\right| \leq 1+\left|a_{n_{1}}\right|+\sum_{k=1}^{n_{1}}\left|a_{k}\right| .$

Theorem $4.5 .3$ If a sequence $\left{a_{n}\right}$ in $\mathbb{F}^{p}$ converges, then the sequence is a Cauchy sequence.

Proof: Let $\varepsilon>0$ be given and suppose $a_{n} \rightarrow a$. Then from the definition of convergence, there exists $n_{\varepsilon}$ such that if $n>n_{\varepsilon}$, it follows that $\left|a_{n}-a\right|<\frac{\varepsilon}{2} .$ Therefore, if $m, n \geq n_{\varepsilon}+1$, it follows that $$ \left|a_{n}-a_{m}\right| \leq\left|a_{n}-a\right|+\left|a-a_{m}\right|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon $$ showing that, since $\varepsilon>0$ is arbitrary, $\left{a_{n}\right}$ is a Cauchy sequence.
The following theorem is very useful.
Theorem 4.5.4 Suppose $\left{a_{n}\right}$ is a Cauchy sequence in $\mathbb{F}^{p}$ and there exists a subsequence, $\left{a_{n_{k}}\right}$ which converges to $a$. Then $\left{a_{n}\right}$ also converges to a.

Proof: Let $\varepsilon>0$ be given. There exists $N$ such that if $m, n>N$, then $\left|a_{m}-a_{n}\right|<$ $\varepsilon / 2$. Also there exists $K$ such that if $k>K$, then $\left|a-a_{n_{k}}\right|<\varepsilon / 2$. Then let $k>$ $\max (K, N)$. Then for such $k$,
$$
\left|a_{k}-a\right| \leq\left|a_{k}-a_{n_{k}}\right|+\left|a_{n_{k}}-a\right|<\varepsilon / 2+\varepsilon / 2=\varepsilon .
$$
This theorem holds in all instances where it makes sense to speak of Cauchy sequences.

柯西序列是“聚集”的序列。这个概念是由博尔扎诺和柯西提出的。这是分析的基本思想。

定义 4.5.1 $\left{a_{n}\right}$ 是一个柯西序列，如果对于所有 $\varepsilon>0$，存在 $n_{\varepsilon}$ 使得每当 $n, m \geq n_{\varepsilon},\left|a_{n}-a_{m}\right|<\varepsilon$。

一个序列是 Cauchy 意味着这些术语“相互聚集”，因为 $m, n$ 变大。

定理 4.5.2 $\mathbb{F}^{p}$ 中柯西序列的项（值）集合是有界的。
证明：在柯西序列的定义中令$\varepsilon=1$，并且令$n>n_{1}$。那么根据定义，$\left|a_{n}-a_{n_{1}}\right|<1$。由三角不等式可知，对于所有 $n>n_{1}，\left|a_{n}\right|<1+\left|a_{n_{1}}\right|$。因此，对于所有 $n，\left|a_{n}\right| \leq 1+\left|a_{n_{1}}\right|+\sum_{k=1}^{n_{1}}\left|a_{k}\right| .$

定理 $4.5 .3$ 如果 $\mathbb{F}^{p}$ 中的序列 $\left{a_{n}\right}$ 收敛，则该序列是柯西序列。

证明：设$\varepsilon>0$ 并假设$a_{n} \rightarrow a$。那么根据收敛性的定义，存在 $n_{\varepsilon}$ 使得如果 $n>n_{\varepsilon}$，那么 $\left|a_{n}-a\right|<\frac {\varepsilon}{2} .$ 因此，如果 $m, n \geq n_{\varepsilon}+1$，则有 $$ \left|a_{n}-a_{m}\right| \leq\left|a_{n}-a\right|+\left|a-a_{m}\right|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2 }=\伐普西隆 $$ 表明，由于 $\varepsilon>0$ 是任意的，$\left{a_{n}\right}$ 是一个柯西序列。
以下定理非常有用。
定理 4.5.4 假设 $\left{a_{n}\right}$ 是 $\mathbb{F}^{p}$ 中的柯西序列，并且存在一个子序列 $\left{a_{n_{ k}}\right}$ 收敛到 $a$。然后 $\left{a_{n}\right}$ 也收敛到 a。

证明：设$\varepsilon>0$。存在 $N$ 使得如果 $m, n>N$，则 $\left|a_{m}-a_{n}\right|<$ $\varepsilon / 2$。也存在$K$，使得如果$k>K$，则$\left|a-a_{n_{k}}\right|<\varepsilon / 2$。然后令$k>$$\max(K,N)$。那么对于这样的$k$，
$$
\left|a_{k}-a\right| \leq\left|a_{k}-a_{n_{k}}\right|+\left|a_{n_{k}}-a\right|<\varepsilon / 2+\varepsilon / 2 =\伐普西隆。
$$
这个定理在所有可以谈论柯西序列的情况下都成立。