0 0

By admin 数学代写 2022年2月23日

When you understand sequences and series of numbers it is easy to consider sequences and series of functions.

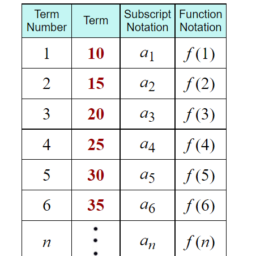
Definition 6.9.1 A sequence of functions is a map defined on $\mathbb{N}$ or some set of integers larger than or equal to a given integer, $m$ which has values which are functions. It is written in the form $\left{f_{n}\right}_{n=m}^{\infty}$ where $f_{n}$ is a function. It is assumed also that the domain of all these functions is the same.

In the above, where do the functions have values? Are they real valued functions? Are they complex valued functions? Are they functions which have values in $\mathbb{R}^{n} ?$ It turns out it does not matter very much and the same definition holds. However, if you like, you can think of them as having values in $\mathrm{F}$. This is the main case of interest here.
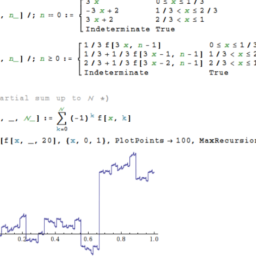
Example 6.9.2 Suppose $f_{n}(x)=x^{n}$ for $x \in[0,1]$. Here is a graph of the functions $f(x)=x, x^{2}, x^{3}, x^{4}, x^{5} .$

Definition 6.9.3 Let $\left{f_{n}\right}$ be a sequence of functions. Then the sequence converges pointwise to a function $f$ if for all $x \in D$, the domain of the functions in the sequence,
$$
f(x)=\lim {n \rightarrow \infty} f{n}(x)
$$
This is always the definition regardless of where the $f_{n}$ have their values.
Thus you consider for each $x \in D$ the sequence $\left{f_{n}(x)\right}$ and if this sequence converges for each $x \in D$, the thing it converges to is called $f(x)$.
Example 6.9.4 In Example 6.9.2 find $\lim {n \rightarrow \infty} f{n}$.
For $x \in[0,1), \lim {n \rightarrow \infty} x^{n}=f{n}(x)=0 .$ At $x=1, f_{n}(1)=1$ for all $n$ so $\lim {n \rightarrow \infty} f{n}(1)=$ 1. Therefore, this sequence of functions converges pointwise to the function $f(x)$ given by $f(x)=0$ if $0 \leq x<1$ and $f(1)=1$. However, given small $\varepsilon>0$, and $n$, there is always some $x$ such that $\left|f(x)-f_{n}(x)\right|>\varepsilon$. Just pick $x$ less than 1 but close to 1 . Then $f(x)=0$ but $f_{n}(x)$ will be close to 1 .

Pointwise convergence is a very inferior thing but sometimes it is all you can get. It’s undesirability is illustrated by Example 6.9.4. The limit function is not continuous although each $f_{n}$ is continuous. Now here is another example of a sequence of functions.
Example 6.9.5 Let $f_{n}(x)=\frac{1}{n} \sin \left(n^{2} x\right)$.
In this example, $\left|f_{n}(x)\right| \leq \frac{1}{n}$ so this function is close to 0 for all $x$ at once provided $n$ is large enough. There is a difference between the two examples just given. They both involve pointwise convergence, but in the second example, the pointwise convergence happens for all $x$ at once. In this example, you have uniform convergence.

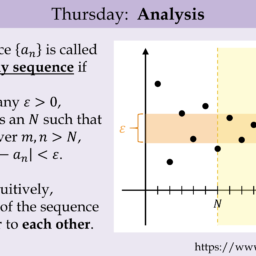
Definition 6.9.6 Let $\left{f_{n}\right}$ be a sequence of functions defined on $D$. Then $\left{f_{n}\right}$ is said to converge uniformly to $f$ if it converges pointwise to $f$ and for every $\varepsilon>0$ there exists $N$ such that for all $n \geq N, \sup {x \in D}\left|f(x)-f{n}(x)\right|<\varepsilon$
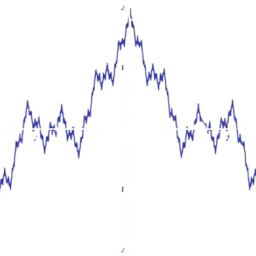
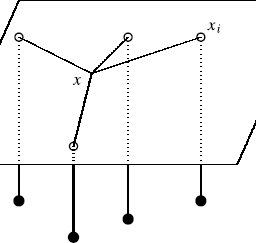
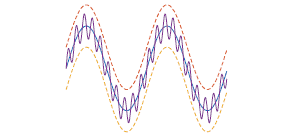
The following picture illustrates the above definition.
The dashed lines define a surall turbe centered about
The dashed lines define a small tube centered about the graph of $f$ and the graph of the function $f_{n}$ fits in this tube for all $n$ sufficiently large. In the picture, the function $f$ is being approximated by $f_{n}$ which is very wriggly.

The reason uniform convergence is desirable is that it drags continuity along with it and imparts this property to the limit function.

Theorem 6.9.7 Let $\left{f_{n}\right}$ be a sequence of functions defined on $D$ which are continuous at $z$ and suppose this sequence converges uniformly to $f$. Then $f$ is also continuous at $z$. If each $f_{n}$ is uniformly continuous on $D$, then $f$ is also uniformly continuous on $D$.

Proof: Let $\varepsilon>0$ be given and pick $z \in D$. By uniform convergence, there exists $N$ such that if $n>N$, then for all $x \in D$,
$$
\left|f(x)-f_{n}(x)\right|<\varepsilon / 3 $$ Pick such an $n$. By assumption, $f_{n}$ is continuous at $z$. Therefore, there exists $\delta>0$ such that if $|z-x|<\delta$ then $$ \left|f_{n}(x)-f_{n}(z)\right|<\varepsilon / 3 $$ It follows that for $|x-z|<\delta$, $$ \begin{aligned} |f(x)-f(z)| & \leq\left|f(x)-f_{n}(x)\right|+\left|f_{n}(x)-f_{n}(z)\right|+\left|f_{n}(z)-f(z)\right| \ &<\varepsilon / 3+\varepsilon / 3+\varepsilon / 3=\varepsilon \end{aligned} $$ which shows that since $\varepsilon$ was arbitrary, $f$ is continuous at $z$. In the case where each $f_{n}$ is uniformly continuous, and using the same $f_{n}$ for which $6.1$ holds, there exists a $\delta>0$ such that if $|y-z|<\delta$, then $\left|f_{n}(z)-f_{n}(y)\right|<\varepsilon / 3$. Then for $|y-z|<\delta$, $$ \begin{aligned} |f(y)-f(z)| & \leq\left|f(y)-f_{n}(y)\right|+\left|f_{n}(y)-f_{n}(z)\right|+\left|f_{n}(z)-f(z)\right| \ &<\varepsilon / 3+\varepsilon / 3+\varepsilon / 3=\varepsilon \end{aligned} $$ This shows uniform continuity of $f$. Definition $6.9 .8$ Let $\left{f_{n}\right}$ be a sequence of functions defined on $D$. Then the sequence is said to be uniformly Cauchy if for every $\varepsilon>0$ there exists $N$ such that whenever $m, n \geq N, \sup {x \in D}\left|f{m}(x)-f_{n}(x)\right|<\varepsilon$.
Then the following theorem follows easily.
Theorem 6.9.9 Let $\left{f_{n}\right}$ be a uniformly Cauchy sequence of $\mathbb{F}$ valued functions defined on $D$. Then there exists $f$ defined on $D$ such that $\left{f_{n}\right}$ converges uniformly to $f$.

Corollary 6.7.3 Suppose $K$ is any closed and bounded set in $\mathbb{F}^{p}$. Then if $f$ is continuous on $K$, it follows that $f$ is uniformly continuous on $K$.

当您了解序列和数字序列时，很容易考虑序列和函数序列。

定义 6.9.1 函数序列是在 $\mathbb{N}$ 或大于或等于给定整数 $m$ 的某些整数集上定义的映射，其值是函数。它以 $\left{f_{n}\right}_{n=m}^{\infty}$ 的形式编写，其中 $f_{n}$ 是一个函数。还假设所有这些函数的域是相同的。

在上面，函数在哪里有值？它们是真正有价值的功能吗？它们是复值函数吗？它们是在 $\mathbb{R}^{n} 中具有值的函数吗？$ 事实证明这并不重要，并且相同的定义成立。但是，如果您愿意，可以将它们视为具有 $\mathrm{F}$ 中的值。这是这里感兴趣的主要案例。
例 6.9.2 假设对于 $x \in[0,1]$，$f_{n}(x)=x^{n}$。这是函数 $f(x)=x, x^{2}, x^{3}, x^{4}, x^{5} .$

定义 6.9.3 令 $\left{f_{n}\right}$ 为函数序列。然后序列逐点收敛到函数 $f$ 如果对于所有 $x \in D$，序列中函数的域，
$$
f(x)=\lim {n \rightarrow \infty} f{n}(x)
$$
无论 $f_{n}$ 的值在哪里，这始终是定义。
因此，您考虑对于每个 $x \in D$ 序列 $\left{f_{n}(x)\right}$ 并且如果这个序列对每个 $x \in D$ 收敛，那么它收敛到的东西是称为$f(x)$。
例 6.9.4 在例 6.9.2 中找到 $\lim {n \rightarrow \infty} f{n}$。
对于 $x \in[0,1)，\lim {n \rightarrow \infty} x^{n}=f{n}(x)=0 .$ 在 $x=1 时，f_{n}(1 )=1$ for all $n$ so $\lim {n \rightarrow \infty} f{n}(1)=$ 1. 因此，这个函数序列逐点收敛到给定的函数 $f(x)$由 $f(x)=0$ 如果 $0 \leq x<1$ 并且 $f(1)=1$。然而，给定小的 $\varepsilon>0$ 和 $n$，总有一些 $x$ 使得 $\left|f(x)-f_{n}(x)\right|>\varepsilon$。只需选择 $x$ 小于 1 但接近 1 。然后 $f(x)=0$ 但 $f_{n}(x)$ 将接近 1 。

逐点收敛是一件非常糟糕的事情，但有时它就是你所能得到的。示例 6.9.4 说明了它的不可取性。尽管每个 $f_{n}$ 都是连续的，但限制函数不是连续的。现在这里是一系列函数的另一个例子。
例 6.9.5 令 $f_{n}(x)=\frac{1}{n} \sin \left(n^{2} x\right)$。
在本例中，$\left|f_{n}(x)\right| \leq \frac{1}{n}$ 所以只要 $n$ 足够大，这个函数对于所有 $x$ 一次都接近于 0。刚刚给出的两个示例之间存在差异。它们都涉及逐点收敛，但在第二个示例中，逐点收敛同时发生在所有 $x$ 上。在此示例中，您具有一致的收敛性。

定义 6.9.6 令 $\left{f_{n}\right}$ 为定义在 $D$ 上的函数序列。那么如果 $\left{f_{n}\right}$ 逐点收敛到 $f$ 并且对于每个 $\varepsilon>0$ 存在 $N$ 使得对于所有$n \geq N, \sup {x \in D}\left|f(x)-f{n}(x)\right|<\varepsilon$
下图说明了上述定义。
虚线定义了一个以
虚线定义了一个以 $f$ 的图形为中心的小管，并且函数 $f_{n}$ 的图形适合所有足够大的 $n$ 的管。在图片中，函数 $f$ 被 $f_{n}$ 逼近，这是非常扭曲的。

需要一致收敛的原因是它会拖累连续性并将此属性赋予极限函数。

定理 6.9.7 令 $\left{f_{n}\right}$ 是定义在 $D$ 上的在 $z$ 处连续的函数序列，并假设该序列一致收敛到 $f$。那么 $f$ 在 $z$ 也是连续的。如果每个 $f_{n}$ 在 $D$ 上一致连续，则 $f$ 在 $D$ 上也是一致连续的。

证明：设$\varepsilon>0$ 并选择$z \in D$。通过一致收敛，存在$N$，使得如果$n>N$，那么对于所有$x\in D$，
$$
\left|f(x)-f_{n}(x)\right|<\varepsilon / 3 $$ 选择这样一个$n$。通过假设，$f_{n}$ 在 $z$ 处是连续的。因此，存在 $\delta>0$ 使得如果 $|z-x|<\delta$ 则 $$ \left|f_{n}(x)-f_{n}(z)\right|<\varepsilon / 3 $$ 由此可见，对于 $|x-z|<\delta$， $$ \开始{对齐} |f(x)-f(z)| & \leq\left|f(x)-f_{n}(x)\right|+\left|f_{n}(x)-f_{n}(z)\right|+\left|f_{n }(z)-f(z)\右| \ &<\varepsilon / 3+\varepsilon / 3+\varepsilon / 3=\varepsilon \end{对齐} $$ 这表明由于 $\varepsilon$ 是任意的，$f$ 在 $z$ 处是连续的。在每个 $f_{n}$ 一致连续的情况下，并且使用 $6.1$ 成立的相同 $f_{n}$，存在 $\delta>0$ 使得如果 $|yz|<\delta $，然后 $\left|f_{n}(z)-f_{n}(y)\right|<\varepsilon / 3$。那么对于 $|y-z|<\delta$，
$$
\开始{对齐}
|f(y)-f(z)| & \leq\left|f(y)-f_{n}(y)\right|+\left|f_{n}(y)-f_{n}(z)\right|+\left|f_{n }(z)-f(z)\右| \
&<\varepsilon / 3+\varepsilon / 3+\varepsilon / 3=\varepsilon
\end{对齐}
$$
这显示了$f$ 的一致连续性。