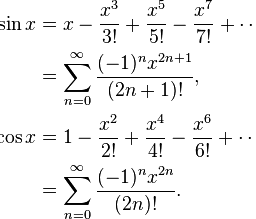0 0

By admin 数学代写 2022年2月23日

9.1 The Integral of 1700 ‘s
Recall the following definition from beginning calculus.
Definition 9.1.1 $\int f(x) d x$ denotes the set of functions $F$ such that $F^{\prime}(x)=$ $f(x)$. These are called antiderivatives.

From the chapter on the derivative, $\int \sum_{k=0}^{n} a_{k} x^{k}=\sum_{k=0}^{n} a_{k} \frac{x^{k+1}}{k+1}+C$ where $C$ is an arbitrary constant.

With this information and the Weierstrass theorem, it is easy to define integrals of continuous functions with all the properties presented in elementary calculus courses. It
${ }^{1}$ Archimedes 287-212 B.C. found areas of curved regions by stuffing them with simple shapes which he knew the area of and taking a limit. He also made fundamental contributions to physics. The story is told about how he determined that a gold smith had cheated the king by giving him a crown which crown and comparing with the amount of water it should have displaced if it had been solid gold.
181
182
CHAPTER 9. INTEGRATION
is an approach which does not depend on Riemann sums yet still gives the fundamental theorem of calculus.

Observation $9.1 .2$ Note that if $F^{\prime}(x)=0$ for $x$ in $(a, b)$ with $F$ continuous on $[a, b]$. Then for $x, y$ in that interval, $F(y)-F(x)=F^{\prime}(z)(y-x)=0(y-x)$ for some $z \in(a, b)$ by the mean value theorem, Corollary $7.8 .3$ so $F$ is a constant. Thus, if $F^{\prime}=G^{\prime}$ on an open interval, $F, G$ continuous on the closed interval, it follows that $F-G$ is a constant and so $F(b)-F(a)=G(b)-G(a)$.

Definition 9.1.3 For the rest of this section, $[a, b]$ will denote the closed interval having end points a and $b$ but a could be larger than $b$. It is written this way to indicate that there is a direction of motion from a to b which will be reflected by the definition of the integral given below. It is an oriented interval.

Definition 9.1.4 For $p(x)$ a polynomial on $[a, b]$, let $P^{\prime}(x)=p(x)$. Thus, by the mean value theorem if $P^{\prime}, \hat{P}^{\prime}$ both equal $p$, it follows that $P(b)-P(a)=\hat{P}(b)-$ $\hat{P}(a)$. Then define $\int_{a}^{b} p(x) d x \equiv P(b)-P(a) .$ If $f \in C([a, b])$, define $\int_{a}^{b} f(x) d x \equiv$ $\lim {n \rightarrow \infty} \int{a}^{b} p_{n}(x) d x$ where $\lim {n \rightarrow \infty}\left|p{n}-f\right|=0$ for
$$
\max {x \in[a, b]}\left|f(x)-p{n}(x)\right| \equiv\left|f-p_{n}\right| .
$$
Such a sequence exists by the Weierstrass approximation theorem, Theorem 6.10.3.
As noted above, this definition is well defined for the integral of polynomials. It remains to show that it is well defined for continuous functions. When this is done, the case of piecewise continuous functions is next.

Proposition $9.1 .5$ The above integral is well defined and satisfies the following properties.

$\int_{a}^{b} f d x=f(\hat{x})(b-a)$ for some $\hat{x}$ between $a$ and $b$. Thus $\left|\int_{a}^{b} f d x\right| \leq|f||b-a|$.
If $f$ is continuous on an interval which contains all necessary intervals,
$$
\int_{a}^{c} f d x+\int_{c}^{b} f d x=\int_{a}^{b} f d x, \text { so } \int_{a}^{b} f d x+\int_{b}^{a} f d x=\int_{b}^{b} f d x=0
$$
If $F(x) \equiv \int_{a}^{x} f d t$, Then $F^{\prime}(x)=f(x)$ so any continuous function has an antiderivative, and for any $a \neq b, \int_{a}^{b} f d x=G(b)-G(a)$ whenever $G^{\prime}=f$ on the open interval determined by $a, b$ and $G$ continuous on the closed interval determined by $a, b$. Also,
If $a<b$, and $f(x) \geq 0$, then $\int_{a}^{b} f d x \geq 0 .$ Also $\left|\int_{a}^{b} f d x\right| \leq\left|\int_{a}^{b}\right| f|d x| .$
$\int_{a}^{b} 1 d x=b-a$.
Proof: First, why is the integral well defined? With notation as in the above definition, the mean value theorem implies
$$
\int_{a}^{b} p(x) d x \equiv P(b)-P(a)=p(\hat{x})(b-a)
$$
9.1. THE INTEGRAL OF $1700^{\prime} S$
183
where $\hat{x}$ is between $a$ and $b$ and so $\left|\int_{a}^{b} p(x) d x\right| \leq|p||b-a| .$ If $\left|p_{n}-f\right| \rightarrow 0$, then
$$
\lim {m, n \rightarrow \infty}\left|p{n}-p_{m}\right| \leq \lim {m, n \rightarrow \infty}\left(\left|p{n}-f\right|+\left|f-p_{m}\right|\right)=0
$$
and so
$$
\begin{aligned}
\left|\int_{a}^{b} p_{n}(x) d x-\int_{a}^{b} p_{m}(x) d x\right| &=\left|\left(P_{n}(b)-P_{n}(a)\right)-\left(P_{m}(b)-P_{m}(a)\right)\right| \
&=\left|\left(P_{n}(b)-P_{m}(b)\right)-\left(P_{n}(a)-P_{m}(a)\right)\right| \
&=\left|\int_{a}^{b}\left(p_{n}-p_{m}\right) d x\right| \leq\left|p_{n}-p_{m}\right||b-a|
\end{aligned}
$$
Thus the limit exists because $\left{\int_{a}^{b} p_{n} d x\right}_{n}$ is a Cauchy sequence and $\mathbb{R}$ is complete.
From $9.1$, 1. holds for a polynomial $p(x)$. Let $\left|p_{n}-f\right| \rightarrow 0$. Then by definition,
$$
\int_{a}^{b} f d x \equiv \lim {n \rightarrow \infty} \int{a}^{b} p_{n} d x=p_{n}\left(x_{n}\right)(b-a)
$$
for some $x_{n}$ in the open interval determined by $(a, b)$. By compactness, there is a further subsequence, still denoted with $n$ such that $x_{n} \rightarrow x \in[a, b]$. Then fixing $m$ such that $\left|f-p_{n}\right|<\varepsilon$ whenever $n \geq m$, assume $n>m .$ Then $\left|p_{m}-p_{n}\right| \leq\left|p_{m}-f\right|+$ $\left|f-p_{n}\right|<2 \varepsilon$ and so
$$
\begin{gathered}
\left|f(x)-p_{n}\left(x_{n}\right)\right| \leq\left|f(x)-f\left(x_{n}\right)\right|+\left|f\left(x_{n}\right)-p_{m}\left(x_{n}\right)\right|+\left|p_{m}\left(x_{n}\right)-p_{n}\left(x_{n}\right)\right| \
\leq\left|f(x)-f\left(x_{n}\right)\right|+\left|f-p_{m}\right|+\left|p_{m}-p_{n}\right|<\left|f(x)-f\left(x_{n}\right)\right|+3 \varepsilon
\end{gathered}
$$
Now if $n$ is still larger, continuity of $f$ shows that $\left|f(x)-p_{n}\left(x_{n}\right)\right|<4 \varepsilon$. Since $\varepsilon$ is arbitrary, $p_{n}\left(x_{n}\right) \rightarrow f(x)$ and so, passing to the limit with this subsequence in $9.2$ yields $1 .$

Now consider 2. It holds for polynomials $p(x)$ obviously. So let $\left|p_{n}-f\right| \rightarrow 0 .$ Then $\int_{a}^{c} p_{n} d x+\int_{c}^{b} p_{n} d x=\int_{a}^{b} p_{n} d x$. Pass to a limit as $n \rightarrow \infty$ and use the definition to get 2 . Also note that $\int_{b}^{b} f(x) d x=0$ follows from the definition.

Next consider 3 . Let $h \neq 0$ and let $x$ be in the open interval determined by $a$ and $b$. Then for small $h$,
$$
\frac{F(x+h)-F(x)}{h}=\frac{1}{h} \int_{x}^{x+h} f(t) d t=f\left(x_{h}\right)
$$
where $x_{h}$ is between $x$ and $x+h$. Let $h \rightarrow 0$. By continuity of $f$, it follows that the limit of the right side exists and so
$$
\lim {h \rightarrow 0} \frac{F(x+h)-F(x)}{h}=\lim {h \rightarrow 0} f\left(x_{h}\right)=f(x)
$$
If $x$ is either end point, the argument is the same except you have to pay attention to the sign of $h$ so that both $x$ and $x+h$ are in $[a, b]$. Thus $F$ is continuous on $[a, b]$ and $F^{\prime}$ exists on $(a, b)$ so if $G$ is an antiderivative,
$$
\int_{a}^{b} f(t) d t \equiv F(b)=F(b)-F(a)=G(b)-G(a)
$$
The claim that the integral is linear is obvious from this. Indeed, if $F^{\prime}=f, G^{\prime}=g$,

9.1 1700 的积分
回想一下从微积分开始的定义。
定义 9.1.1 $\int f(x) d x$ 表示函数集合 $F$ 使得 $F^{\prime}(x)=$ $f(x)$。这些被称为抗衍生物。

从导数一章，$\int \sum_{k=0}^{n} a_{k} x^{k}=\sum_{k=0}^{n} a_{k} \frac{x ^{k+1}}{k+1}+C$ 其中 $C$ 是任意常数。

有了这些信息和 Weierstrass 定理，就很容易定义具有初等微积分课程中所有性质的连续函数的积分。它
${ }^{1}$ 阿基米德 287-212 B.C.通过用他知道面积并限制的简单形状填充弯曲区域来找到弯曲区域的区域。他还对物理学做出了基础性贡献。故事讲述了他如何确定一个金匠欺骗了国王，给了他一顶王冠，并与如果它是纯金的话应该排出的水量进行比较。
181
182
第 9 章集成
是一种不依赖于黎曼和但仍给出微积分基本定理的方法。

观察 $9.1 .2$ 注意如果 $F^{\prime}(x)=0$ for $x$ in $(a, b)$ 且 $F$ 在 $[a, b]$ 上连续。然后对于该区间内的 $x, y$，对于某些 $z \in(a, b )$ 由中值定理推论 $7.8 .3$ 所以 $F$ 是一个常数。因此，如果 $F^{\prime}=G^{\prime}$ 在开区间上，$F, G$ 在闭区间上连续，则 $FG$ 是一个常数，因此 $F(b) -F(a)=G(b)-G(a)$。

定义 9.1.3 对于本节的其余部分，$[a, b]$ 将表示具有端点 a 和 $b$ 但 a 可能大于 $b$ 的闭区间。这样写是为了表明存在从 a 到 b 的运动方向，这将通过下面给出的积分的定义来反映。这是一个定向区间。

定义 9.1.4 对于 $p(x)$ 一个关于 $[a, b]$ 的多项式，令 $P^{\prime}(x)=p(x)$。因此，根据中值定理，如果 $P^{\prime}、\hat{P}^{\prime}$ 都等于 $p$，则 $P(b)-P(a)=\hat{ P}(b)-$$\hat{P}(a)$。然后定义 $\int_{a}^{b} p(x) dx \equiv P(b)-P(a) .$ 如果 $f \in C([a, b])$，定义 $\int_{ a}^{b} f(x) dx \equiv$ $\lim {n \rightarrow \infty} \int{a}^{b} p_{n}(x) dx$ 其中 $\lim {n \rightarrow \infty}\left|p{n}-f\right|=0$ 为
$$
\max {x \in[a, b]}\left|f(x)-p{n}(x)\right| \equiv\left|f-p_{n}\right| .
$$
Weierstrass 逼近定理定理 6.10.3 存在这样的序列。
如上所述，这个定义对于多项式的积分是很好的定义。它仍然表明它对于连续函数是很好定义的。完成后，接下来是分段连续函数的情况。

命题 $9.1 .5$ 上面的积分是很好定义的并且满足以下性质。

$\int_{a}^{b} f d x=f(\hat{x})(b-a)$ 对于 $a$ 和 $b$ 之间的一些 $\hat{x}$。因此 $\left|\int_{a}^{b} f d x\right| \leq|f||b-a|$。
如果 $f$ 在包含所有必要区间的区间上是连续的，
$$
\int_{a}^{c} fd x+\int_{c}^{b} fdx=\int_{a}^{b} fdx, \text { 所以 } \int_{a}^{b} fd x+\ int_{b}^{a} fdx=\int_{b}^{b} fdx=0
$$
如果 $F(x) \equiv \int_{a}^{x} fdt$，则 $F^{\prime}(x)=f(x)$ 所以任何连续函数都有一个反导数，并且对于任何$a \neq b, \int_{a}^{b} fdx=G(b)-G(a)$ 每当 $G^{\prime}=f$ 在由 $a, b$ 和$G$ 在由 $a, b$ 确定的闭区间上连续。还，
如果$a<b$，且$f(x) \geq 0$，则$\int_{a}^{b} fdx \geq 0 .$ 还有$\left|\int_{a}^{b} fdx \对| \leq\left|\int_{a}^{b}\right| f|dx| .$
$\int_{a}^{b} 1 d x=b-a$。
证明：首先，为什么积分是明确定义的？使用上述定义中的符号，均值定理意味着
$$
\int_{a}^{b} p(x) d x \equiv P(b)-P(a)=p(\hat{x})(b-a)
$$
9.1。 1700 美元的积分^{\prime} S$
183
其中 $\hat{x}$ 在 $a$ 和 $b$ 之间，所以 $\left|\int_{a}^{b} p(x) d x\right| \leq|p||b-a| .$ 如果 $\left|p_{n}-f\right| \rightarrow 0$，然后
$$
\lim {m, n \rightarrow \infty}\left|p{n}-p_{m}\right| \leq \lim {m, n \rightarrow \infty}\left(\left|p{n}-f\right|+\left|f-p_{m}\right|\right)= 0
$$
所以
$$
\开始{对齐}
\left|\int_{a}^{b} p_{n}(x) d x-\int_{a}^{b} p_{m}(x) d x\right| &=\left|\left(P_{n}(b)-P_{n}(a)\right)-\left(P_{m}(b)-P_{m}(a)\right)\right | \
&=\left|\left(P_{n}(b)-P_{m}(b)\right)-\left(P_{n}(a)-P_{m}(a)\right)\right | \
&=\left|\int_{a}^{b}\left(p_{n}-p_{m}\right) d x\right| \leq\left|p_{n}-p_{m}\right||b-a|
\end{对齐}
$$
因此存在极限是因为 $\left{\int_{a}^{b} p_{n} d x\right}_{n}$ 是一个柯西序列并且 $\mathbb{R}$ 是完整的。
从 $9.1$ 开始，对于多项式 $p(x)$，1. 成立。让 $\left|p_{n}-f\right| \rightarrow 0$。那么根据定义，
$$
\int_{a}^{b} fdx \equiv \lim {n \rightarrow \infty} \int{a}^{b} p_{n} dx=p_{n}\left(x_{n}\right )(巴)
$$
对于由 $(a, b)$ 确定的开区间中的一些 $x_{n}$。通过紧凑性，还有一个子序列，仍然用 $n$ 表示，使得 $x_{n