Stirling’s Formula

In this section is an elementary approach to Stirlings formula. This formula is an asymptotic approximation for $n !$. It is quite old, dating to about 1730 . The approach followed here is like the one in the Calculus book of Courant found in the references. Later I will give a different one found in [23]. See also [9].

To begin with is a simple lemma which really depends on the shape of the graph of $t \rightarrow \ln t$.
9.7. STIRLING’S FORMULA
203
Lemma 9.7.1 For n a positive integer,
$$
\frac{1}{2}(\ln (n+1)+\ln (n)) \leq \int_{n}^{n+1} \ln (t) d t \leq \ln \left(n+\frac{1}{2}\right)
$$
Proof: Consider the following picture.
There are two trapezoids, the area of the larger one is larger than $\int_{n}^{n+1} \ln (t) d t$ and the area of the smaller being smaller than this integral. The equation of the line which forms the top of the large trapezoid is
$$
y-\ln \left(n+\frac{1}{2}\right)=\frac{1}{n+\frac{1}{2}}\left(x-\left(n+\frac{1}{2}\right)\right)
$$
Thus the area of the large trapezoid is obtained by averaging the two vertical sides and multiplying by the length of the base which is 1 . This is easily found to be $\ln \left(n+\frac{1}{2}\right)$. Then the area of the smaller trapezoid is obtained also as the average of the two vertical sides times the length of the base which is $\frac{1}{2}(\ln (n+1)+\ln (n))$.
Thus a lower approximation for $\int_{1}^{n} \ln (t) d t$, denoted as $T_{n}$ is
$$
T_{n} \equiv \sum_{k=1}^{n-1} \frac{1}{2}(\ln (k)+\ln (k+1))
$$
Then, from the above lemma,
$$
\begin{aligned}
\int_{1}^{n} \ln (t) d t-T_{n} &=\sum_{k=1}^{n-1} \int_{k}^{k+1} \ln (t) d t-\sum_{k=1}^{n-1} \frac{1}{2}(\ln (k)+\ln (k+1)) \
& \leq \sum_{k=1}^{n-1} \ln \left(k+\frac{1}{2}\right)-\sum_{k=1}^{n-1} \frac{1}{2}(\ln (k)+\ln (k+1))
\end{aligned}
$$
$$
\begin{aligned}
&=\sum_{k=1}^{n-1} \frac{1}{2}\left(\ln \left(k+\frac{1}{2}\right)-\ln (k)\right)-\sum_{k=1}^{n-1} \frac{1}{2}\left(\ln (k+1)-\ln \left(k+\frac{1}{2}\right)\right) \
&\leq \sum_{k=1}^{n-1} \frac{1}{2}\left(\ln (k)-\ln \left(k-\frac{1}{2}\right)\right)-\sum_{k=1}^{n-1} \frac{1}{2}\left(\ln (k+1)-\ln \left(k+\frac{1}{2}\right)\right) \
&=\sum_{k=0}^{n-2} \frac{1}{2}\left(\ln (k+1)-\ln \left(k+\frac{1}{2}\right)\right)-\sum_{k=1}^{n-1} \frac{1}{2}\left(\ln (k+1)-\ln \left(k+\frac{1}{2}\right)\right) \
&=\frac{1}{2}\left(\ln (1)-\ln \left(\frac{1}{2}\right)\right)-\frac{1}{2}\left(\ln (n)-\ln \left(n-\frac{1}{2}\right)\right) \leq \frac{\ln (2)}{2}
\end{aligned}
$$
CHAPTER 9. INTEGRATION
Now this shows that $\left{\int_{1}^{n} \ln (t) d t-T_{n}\right}_{n=1}^{\infty}$ is an increasing sequence which is bounded above and so it must converge to some real number $\alpha$.
$$
\begin{aligned}
\exp \left(T_{n}\right) &=\prod_{k=1}^{n-1} \exp \left(\frac{1}{2}(\ln (k)+\ln (k+1))\right)=\prod_{k=1}^{n-1}(k(k+1))^{1 / 2} \
&=(1 \cdot 2)^{1 / 2}(2 \cdot 3)^{1 / 2} \ldots((n-1) \cdot n)^{1 / 2}=(n-1) ! \sqrt{n}=n ! n^{-1 / 2}
\end{aligned}
$$
Therefore, doing the integral $\int_{1}^{n} \ln (t) d t$ and taking the exponential of the expression,
$$
\lim {n \rightarrow \infty} \exp \left((n \ln (n)-n)-T{n}\right)=\lim {n \rightarrow \infty} \frac{e^{(n \ln (n)-n)}}{n^{-1 / 2} n !}=\lim {n \rightarrow \infty} \frac{n^{n+\frac{1}{2}} e^{-n}}{n !}=e^{\alpha}
$$
This has proved the following lemma.
Lemma 9.7.2 There exists a positive number c such that
$$
\lim {n \rightarrow \infty} \frac{n !}{n^{n+(1 / 2)} e^{-n{c}}}=1 \text {. }
$$
In many applications, the above is enough. However, the constant can be found. There are various ways to show that this constant $c$ equals $\sqrt{2 \pi}$. The version given here also includes a formula which is interesting for its own sake.

Using integration by parts, it follows that whenever $n$ is a positive integer larger than 1
$$
\int_{0}^{\pi / 2} \sin ^{n}(x) d x=\frac{n-1}{n} \int_{0}^{\pi / 2} \sin ^{n-2}(x) d x
$$
Lemma 9.7.3 For $m \geq 1$,
$$
\begin{aligned}
\int_{0}^{\pi / 2} \sin ^{2 m}(x) d x &=\frac{(2 m-1) \cdots 1}{2 m(2 m-2) \cdots 2} \frac{\pi}{2} \
\int_{0}^{\pi / 2} \sin ^{2 m+1}(x) d x &=\frac{(2 m)(2 m-2) \cdots 2}{(2 m+1)(2 m-1) \cdots 3}
\end{aligned}
$$
Proof: Consider the first formula in the case where $m=1$. From beginning calculus,
$$
\int_{0}^{\pi / 2} \sin ^{2}(x) d x=\frac{\pi}{4}=\frac{1}{2} \frac{\pi}{2}
$$
so the formula holds in this case. Suppose it holds for $m$. Then from the above reduction identity and induction,
$$
\begin{aligned}
\int_{0}^{\pi / 2} \sin ^{2 m+2}(x) d x &=\frac{2 m+1}{2(m+1)} \int_{0}^{\pi / 2} \sin ^{2 m}(x) d x \
&=\frac{2 m+1}{2(m+1)} \frac{(2 m-1) \cdots 1}{2 m(2 m-2) \cdots 2} \frac{\pi}{2} .
\end{aligned}
$$

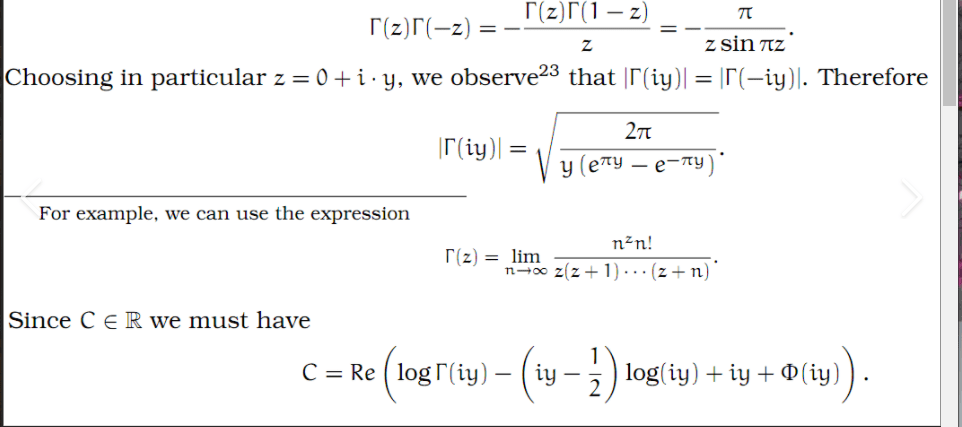
9.7 斯特林公式
在本节中是斯特林公式的基本方法。这个公式是 $n !$ 的渐近近似。它相当古老，可追溯到 1730 年左右。这里采用的方法类似于参考文献中的 Courant 微积分书中的方法。稍后我将给出一个在 [23] 中找到的不同的。另见[9]。

首先是一个简单的引理，它实际上取决于 $t \rightarrow \ln t$ 的图形的形状。
9.7。斯特林公式
203
引理 9.7.1 对于 n 一个正整数，
$$
\frac{1}{2}(\ln (n+1)+\ln (n)) \leq \int_{n}^{n+1} \ln (t) dt \leq \ln \left(n+ \frac{1}{2}\右）
$$
证明：考虑下图。
有两个梯形，较大的面积大于$\int_{n}^{n+1} \ln (t) d t$，较小的面积小于这个积分。形成大梯形顶部的直线方程为
$$
y-\ln \left(n+\frac{1}{2}\right)=\frac{1}{n+\frac{1}{2}}\left(x-\left(n+\frac{1} {2}\右）\右）
$$
因此，大梯形的面积是通过平均两个垂直边并乘以底边的长度（即 1 ）来获得的。很容易找到 $\ln\left(n+\frac{1}{2}\right)$。然后得到较小梯形的面积，也就是两个垂直边的平均值乘以底边的长度，即 $\frac{1}{2}(\ln (n+1)+\ln (n))美元。
因此 $\int_{1}^{n} \ln (t) d t$ 的下近似值，表示为 $T_{n}$ 是
$$
T_{n} \equiv \sum_{k=1}^{n-1} \frac{1}{2}(\ln (k)+\ln (k+1))
$$
那么，根据上面的引理，
$$
\开始{对齐}
\int_{1}^{n} \ln (t) d t-T_{n} &=\sum_{k=1}^{n-1} \int_{k}^{k+1} \ln ( t) d t-\sum_{k=1}^{n-1} \frac{1}{2}(\ln (k)+\ln (k+1)) \
& \leq \sum_{k=1}^{n-1} \ln \left(k+\frac{1}{2}\right)-\sum_{k=1}^{n-1} \frac{ 1}{2}(\ln (k)+\ln (k+1))
\end{对齐}
$$
$$
\开始{对齐}
&=\sum_{k=1}^{n-1} \frac{1}{2}\left(\ln \left(k+\frac{1}{2}\right)-\ln (k)\右)-\sum_{k=1}^{n-1} \frac{1}{2}\left(\ln (k+1)-\ln \left(k+\frac{1}{2}\是的是的） \
&\leq \sum_{k=1}^{n-1} \frac{1}{2}\left(\ln (k)-\ln \left(k-\frac{1}{2}\right )\right)-\sum_{k=1}^{n-1} \frac{1}{2}\left(\ln (k+1)-\ln \left(k+\frac{1}{2 }\是的是的） \
&=\sum_{k=0}^{n-2} \frac{1}{2}\left(\ln (k+1)-\ln \left(k+\frac{1}{2}\right )\right)-\sum_{k=1}^{n-1} \frac{1}{2}\left(\ln (k+1)-\ln \left(k+\frac{1}{2 }\是的是的） \
&=\frac{1}{2}\left(\ln (1)-\ln \left(\frac{1}{2}\right)\right)-\frac{1}{2}\left( \ln (n)-\ln \left(n-\frac{1}{2}\right)\right) \leq \frac{\ln (2)}{2}
\end{对齐}
$$
第 9 章集成
现在这表明 $\left{\int_{1}^{n} \ln (t) d t-T_{n}\right}_{n=1}^{\infty}$ 是一个递增序列它是有界的，因此它必须收敛到某个实数 $\alpha$。
$$
\开始{对齐}
\exp \left(T_{n}\right) &=\prod_{k=1}^{n-1} \exp \left(\frac{1}{2}(\ln (k)+\ln ( k+1))\right)=\prod_{k=1}^{n-1}(k(k+1))^{1 / 2} \
&=(1 \cdot 2)^{1 / 2}(2 \cdot 3)^{1 / 2} \ldots((n-1) \cdot n)^{1 / 2}=(n-1) ！ \sqrt{n}=n ！ n^{-1 / 2}
\end{对齐}
$$
因此，做积分 $\int_{1}^{n} \ln (t) d t$ 并取表达式的指数，
$$
\lim {n \rightarrow \infty} \exp \left((n \ln (n)-n)-T{n}\right)=\lim {n \rightarrow \infty} \frac{e^{ (n \ln (n)-n)}}{n^{-1 / 2} n !}=\lim {n \rightarrow \infty} \frac{n^{n+\frac{1}{2} } e^{-n}}{n !}=e^{\alpha}
$$
这证明了以下引理。
引理 9.7.2 存在一个正数 c 使得
$$
\lim {n \rightarrow \infty} \frac{n !}{n^{n+(1 / 2)} e^{-n{c}}}=1 \text {. }
$$
在许多应用中，以上就足够了。但是，可以找到常数。有多种方法可以证明这个常数 $c$ 等于 $\sqrt{2 \pi}$。这里给出的版本还包括一个有趣的公式。

使用分部积分，只要 $n$ 是大于 1 的正整数
$$
\int_{0}^{\pi / 2} \sin ^{n}(x) dx=\frac{n-1}{n} \int_{0}^{\pi / 2} \sin ^{n -2}(x) dx
$$
引理 9.7.3 对于 $m \geq 1$，
$$
\开始{对齐}
\int_{0}^{\pi / 2} \sin ^{2 m}(x) dx &=\frac{(2 m-1) \cdots 1}{2 m(2 m-2) \cdots 2 } \frac{\pi}{2} \
\int_{0}^{\pi / 2} \sin ^{2 m+1}(x) dx &=\frac{(2 m)(2 m-2) \cdots 2}{(2 m+1 )(2 m-1) \cdots 3}
\end{对齐}
$$
证明：考虑 $m=1$ 的情况下的第一个公式。从微积分开始，
$$
\int_{0}^{\pi / 2} \sin ^{2}(x) d x=\frac{\pi}{4}=\frac{1}{2} \frac{\pi}{2}
$$
所以这个公式在这种情况下成立。假设它持有$m$。然后由上述归约恒等式和归纳，
$$
\开始{对齐}
\int_{0}^{\pi / 2} \sin ^{2 m+2}(x) dx &=\frac{2 m+1}{2(m+1)} \int_{0}^{ \pi / 2} \sin ^{2 m}(x) dx \
&=\frac{2 m+1}{2(m+1)} \frac{(2 m-1) \cdots 1}{2 m(2 m-2) \cdots 2} \frac{\pi} {2} 。
\end{对齐}
$$