统计代写| Cumulative distribution functions stat代写
统计代考
$3.6$ Cumulative distribution functions
Another function that describes the distribution of an r.v. is the cumulative distribution function (CDF). Unlike the PMF, which only discrete r.v.s possess, the CDF is defined for all r.v.s.
Random variables and their distributions 121
Definition 3.6.1. The cumulative distribution function CrM) of an rov. function $F_{X}$ given by $F_{X}(x)=P(X \leq x)$. When there is no risk of ambiguity, we
sometimes drop the subscript and just write F (or some other letter) for a CDF.
The next example demonstrates that for discrete r.v.s, we can freely comvert between
Fow ind PMIF’
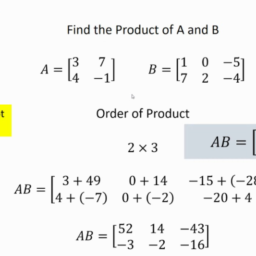
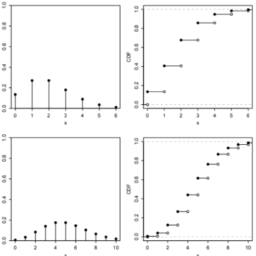
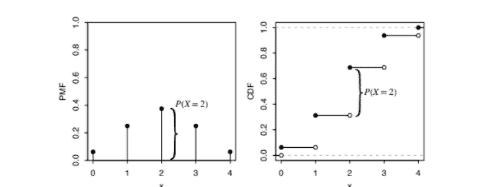
Example 3.6.2. Let $X \sim \operatorname{Bin}(4,1 / 2)$. Figure $3.8$ shows the PMF and CDF of $X$.
FIGURE $3.8$ Bin(4,1/2) PMF and CDF. The height of the vertical bar $P(X=2)$ in the PMF is also the height of the jump in the CDF at 2 .
- From PMF to CDF: To find $P(X \leq 1.5)$, which is the CDF evaluated at 1.5, we
sum the PMF over all values of the support that are less than or equal to $1.5$ :
$$
P(X \leq 1.5)=P(X=0)+P(X=1)=\left(\frac{1}{2}\right)^{4}+4\left(\frac{1}{2}\right)^{4}=\frac{5}{16}
$$
Similarly, the value of the CDF at an arbitrary point $x$ is the sum of the heights of the vertical bars of the PMF at values less than or equal to $x$. - From CDF to PWF: The CDF of a discrete r.v, consists of jumps and flat regions. The hejght of a jump in the CDF at $x$ is equal to the value of the PMF at $x$. For example, in Fligure $3.8$, the height of the jump in the CDF at 2 is the same as the height of the corresponding vertical bar in the PMF; this is indicated in the figure with curly hraces. The flat regions of the CDF correspond to values outside the support of $X$, so the PMF is equal to 0 in those regions.
Valid CDFs sat isfy the following criteria.
Theorem 3.6.3 (Valid CDFs). Any CDF F has the following properties. - Increasing: If $x_{1} \leq x_{2}$, then $F\left(x_{1}\right) \leq F\left(x_{2}\right)$
The first criterion is true since the event $\left{X \leq x_{1}\right}$ is a subset of the event $\left{X \leq x_{2}\right}$, so. $P\left(X \leq x_{1}\right) \leq P\left(X \leq x_{2}\right)$.
$P(\lambda \leq-1) \leq P\left(X \leq x_{2}\right)$
For the second criterion, note that
$$
P(X \leq x)=P(X \leq\lfloor x\rfloor){+} $$ where $[x]$ is the greatest integer less than or equal to $x .$ For example, $P(X \leq 4.9)=$ $P(X \leq 4)$ since $X$ is integer-vulued. So $F(a+b)=F(a)$ for any $b>0$ that is small enough so that $a+b<\lfloor a\rfloor+1$, e.g. for $a=4.9$, this holds for $0{x \rightarrow a^{+}} F(x)$ (in fact, it’s much stronger since it says $F(x)$ cyuals
F(a) when $x$ is close enough to a and on the right).
For the third criterion, we have $F(x)=0$ for $x<0$, and
统计代考
$3.6$ 累积分布函数
另一个描述房车分布的函数。是累积分布函数 (CDF)。与仅离散 r.v.s 拥有的 PMF 不同,CDF 是为所有 r.v.s 定义的。
随机变量及其分布 121
定义 3.6.1。一个 rov 的累积分布函数 CrM)。由 $F_{X}(x)=P(X \leq x)$ 给出的函数 $F_{X}$。当没有歧义的风险时,我们
有时去掉下标,只为 CDF 写 F(或其他字母)。
下一个示例演示对于离散 r.v.s,我们可以在
流动性PMIF’
示例 3.6.2。设 $X \sim \operatorname{Bin}(4,1 / 2)$。图 $3.8$ 显示了 $X$ 的 PMF 和 CDF。
图 $3.8$ Bin(4,1/2) PMF 和 CDF。 PMF 中竖线 $P(X=2)$ 的高度也是 CDF 在 2 处跳跃的高度。
- 从 PMF 到 CDF:要找到 $P(X \leq 1.5)$,这是评估为 1.5 的 CDF,我们
将 PMF 与小于或等于 $1.5$ 的所有支持值相加:
$$
P(X \leq 1.5)=P(X=0)+P(X=1)=\left(\frac{1}{2}\right)^{4}+4\left(\frac{1} {2}\right)^{4}=\frac{5}{16}
$$
类似地,任意点 $x$ 处的 CDF 值是 PMF 在小于或等于 $x$ 处的垂直条的高度之和。 - 从 CDF 到 PWF:离散 r.v 的 CDF 由跳跃和平坦区域组成。 CDF 在 $x$ 处的跳跃高度等于 PMF 在 $x$ 处的值。例如,在Fligure $3.8$中,CDF中2处的跳跃高度与PMF中对应竖线的高度相同;这在图中用花边表示。 CDF 的平坦区域对应于 $X$ 支持之外的值,因此这些区域中的 PMF 等于 0。
有效的 CDF 满足以下标准。
定理 3.6.3(有效 CDF)。任何 CDF F 都具有以下属性。 - 增加:如果 $x_{1} \leq x_{2}$,则 $F\left(x_{1}\right) \leq F\left(x_{2}\right)$
第一个标准为真,因为事件 $\left{X \leq x_{1}\right}$ 是事件 $\left{X \leq x_{2}\right}$ 的子集,所以. $P\left(X \leq x_{1}\right) \leq P\left(X \leq x_{2}\right)$。
$P(\lambda \leq-1) \leq P\left(X \leq x_{2}\right)$
对于第二个标准,请注意
$$
P(X \leq x)=P(X \leq\lfloor x\rfloor){+} $$ 其中 $[x]$ 是小于或等于 $x 的最大整数。$ 例如,$P(X \leq 4.9)=$ $P(X \leq 4)$ 因为 $X$ 是整数值。所以 $F(a+b)=F(a)$ 对于任何足够小的 $b>0$ 使得 $a+b<\lfloor a\rfloor+1$,例如对于 $a=4.9$,这适用于 $0{x \rightarrow a^{+}} F(x)$ (事实上,它更强大,因为它说 $F(x)$ cyuals
F(a) 当 $x$ 足够靠近 a 并且在右边)。
对于第三个标准,对于 $x<0$,我们有 $F(x)=0$,并且
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。