统计代写| Distributions and probability mass functions stat代写
统计代考
$3.2$ Distributions and probability mass functions
There are two main types of random variables used in practice: discrete r.v.s an continuous r.v.s. In this chapter and the next, our focus is on discrete r.v.s. Con tinuous r.v.s are introduced in Chapter 5 .
Definition 3.2.1 (Discrete random variable). A random variable $X$ is said to b discrete if there is a finite list of values $a_{1}, a_{2}, \ldots, a_{n}$ or an infinite list of value $a_{1}, a_{2}, \ldots$ such that $P\left(X=a_{j}\right.$ for some $\left.j\right)=1$. If $X$ is a discrete r.v., then th
Random variables and their distributions
finite or countably infinite set of values $x$ such that $P(X=x)>0$ is called th support of $X$.
Most commonly in applications, the support of a discrete r.v, is a set of integers In contrast, a continuous r.v, can take on any real value in an interval (possibl even the entire real line); such r.v.s are defined more precisely in Chapter $5 .$ is also possible to have an r.v. that is a hybrid of discrete and continuous, suc as by flipping a coin and then generating a discrete r.v. if the coin lands Head understanding such r.y.s is to understand discrete and continuous r. $y .8 .$
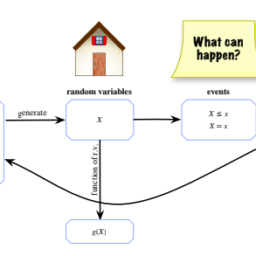
Given a randem variable, we weuld like to be able to describe its behavior using th language of probability. For example, we might want to answer questions about th probability that the r.v. will fall into a given range: if $L$ is the lifetime earnings a randomly chosen U.S. college graduate, what is the probability that $L$ exceeds million dollars? If $M$ is the number of major earthquakes in California in the nex five years, what is the probability that $M$ equals 0 ?
The distribution of a random variable provides the answers to these questions: specifies the probabilities of all events associated with the r.v., such as the probi bility of it equaling 3 and the probability of it being at least 110 . We will see tha there are several equivalent ways to express the distribution of an r.v. For a discret $\mathrm{r}_{\mathrm{V}}$, the most natural way to do so is with a probability mass function, which w now define,
Definition $3.2 .2$ (Probability mass function). The probability mass function (PMF) of a discrete r.v. $X$ is the function $p_{X}$ given by $p_{X}(x)=P(X=x)$. Not that this is positive if $x$ is in the support of $X$, and 0 otherwise.
w $3.2 .3 .$ In writing $P(X=x)$, we are using $X=x$ to denote an event, consisting of all outcomes $s$ to which $X$ assigns the number $x$. This event is also written a ${X=x} ;$ formally, ${X=x}$ is defined as ${s \in S: X(s)=x}$, but writing ${X=x$ is shorter and more intuitive, Going back to Example 3,1,2, if $X$ is the numbe of Heads in two fair coin tosses, then ${X=1}$ consists of the sample outcome $H T$ and $T H$, which are the two outcomes to which $X$ assigns the number 1. Sinc ${H T, T H}$ is a subset of the sample space, it is an event. So it makes sense to tal ${H T, T H}$ is a subset of the sumple space, it is an event. So it makes sense to tal about $P(X=1)$, or more generally, $P(X=x)$. If ${X=x}$ were anything othe than an event, it would make no sense to calculate its probability! It does not make sense to write ” $P(X) “$; we can only take the probability of an event, not of an r.
Let’s look at a few examples of PMFs.
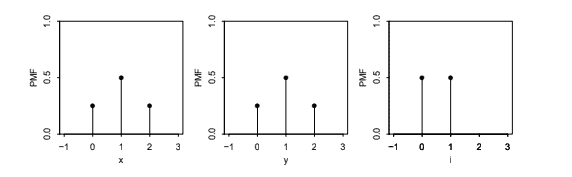
Example $3.2 .4$ (Coin tosses continued). In this example we’ll find the PMFs all the random variables in Example 3.1.2, the example with two fair coin tosses Here are the r.v.s we defined, along with their PMEs:
- $X$, the number of Heads. Since $X$ equals 0 if TT occurs, 1 if HT or TH occurs
108
and 2 if $H H$ occurs, the PMF of $X$ is the function $p_{X}$ given by
$$
\begin{aligned}
&p_{X}(0)=P(X=0)=1 / 4 \
&p_{X}(1)=P(X=1)=1 / 2 \
&p_{X}(2)=P(X=2)=1 / 4
\end{aligned}
$$
and $p_{X}(x)=0$ for all other values of $x$.
$P(Y=y)=P(2-X=y)=P(X=2-y)=p_{X}(2-y)$
统计代考
$3.2$ 分布和概率质量函数
实际使用的随机变量有两种主要类型:离散 r.v.s 和连续 r.v.s。在本章和下一章中,我们的重点是离散 r.v.s。连续 r.v.s 在第 5 章中介绍。
定义 3.2.1(离散随机变量)。如果存在值 $a_{1}、a_{2}、\ldots、a_{n}$ 的有限列表或值 $a_{1} 的无限列表,则随机变量 $X$ 被称为 b 离散的, a_{2}, \ldots$ 使得 $P\left(X=a_{j}\right.$ for some $\left.j\right)=1$。如果 $X$ 是一个离散的 r.v.,那么
随机变量及其分布
有限或可数无限的值 $x$ 集合使得 $P(X=x)>0$ 被称为 $X$ 的支持。
在应用程序中最常见的是,离散 r.v 的支持是一组整数。相比之下,连续 r.v 可以在一个区间内取任何实数(甚至可能是整个实数线);这样的 r.v.s 在第 5 章中有更准确的定义。$ 也可能有一个 r.v.。这是离散和连续的混合体,例如通过掷硬币然后生成离散的 r.v.如果硬币落到头上,理解这样的 r.y.s 就是理解离散和连续的 r。 $y .8 .$
给定一个随机变量,我们希望能够使用概率语言来描述它的行为。例如,我们可能想回答有关 r.v. 的概率的问题。将落入给定范围内:如果 $L$ 是随机选择的美国大学毕业生的终生收入,那么 $L$ 超过百万美元的概率是多少?如果 $M$ 是未来五年加利福尼亚发生大地震的次数,$M$ 等于 0 的概率是多少?
随机变量的分布提供了这些问题的答案:指定与 r.v. 相关的所有事件的概率,例如它等于 3 的概率和它至少为 110 的概率。我们将看到有几种等效的方式来表达 r.v. 的分布。对于离散的 $\mathrm{r}_{\mathrm{V}}$,最自然的方法是使用概率质量函数,现在定义为:
定义 $3.2 .2$(概率质量函数)。离散 r.v. 的概率质量函数 (PMF)。 $X$ 是由 $p_{X}(x)=P(X=x)$ 给出的函数 $p_{X}$。如果 $x$ 在 $X$ 的支持下,这并不是正数,否则为 0。
w $3.2 .3 .$ 在编写 $P(X=x)$ 时,我们使用 $X=x$ 来表示一个事件,该事件由 $X$ 赋予数字 $x$ 的所有结果 $s$ 组成。这个事件也写成 ${X=x} ;$ 形式上,${X=x}$ 定义为 ${s \in S: X(s)=x}$,但是写成${X=x$ 更短更直观,回到示例 3,1,2,如果 $X$ 是两次公平抛硬币中正面的数量,则 ${X=1}$ 由样本结果 $HT$ 和 $TH$,这是 $X$ 分配数字 1 的两个结果。 Sinc ${HT, TH}$ 是样本空间的子集,它是一个事件。所以 tal ${H T, T H}$ 是和空间的一个子集是有意义的,它是一个事件。所以计算 $P(X=1)$,或更一般地说,$P(X=x)$ 是有意义的。如果 ${X=x}$ 不是一个事件,那么计算它的概率是没有意义的!写“$P(X)”$没有意义;我们只能取事件的概率,而不是 r。
让我们看几个 PMF 的例子。
示例 $3.2 .4$(继续抛硬币)。在这个例子中,我们将在例子 3.1.2 中找到所有随机变量的 PMF,这个例子有两次公平的抛硬币 下面是我们定义的 r.v.s,以及它们的 PME:
- $X$,正面数。因为如果出现 TT,$X$ 等于 0,如果出现 HT 或 TH,则为 1
108
和 2 如果出现 $H H$,则 $X$ 的 PMF 是由下式给出的函数 $p_{X}$
$$
\开始{对齐}
&p_{X}(0)=P(X=0)=1 / 4 \
&p_{X}(1)=P(X=1)=1 / 2 \
&p_{X}(2)=P(X=2)=1 / 4
\end{对齐}
$$
对于 $x$ 的所有其他值,$p_{X}(x)=0$。
$P(Y=y)=P(2-X=y)=P(X=2-y)=p_{X}(2-y)$
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。