统计代写| Poisson stat代写
统计代考
4.7 Poisson
The last discrete distribution that we’ll introduce in this chapter is the Poisson, which is an extremely popular distribution for modeling discrete data. We’ll introduce its PMF, mean, and variance, and then discuss its story in more detail.
Expectation
175
Definition 4.7.1 (Poisson distribution). An r.v. $X$ has the Poisson distribution with parameter $\lambda$, where $\lambda>0$, if the PMF of $X$ is
$$
P(X=k)=\frac{e^{-\lambda} \lambda^{k}}{k !}, \quad k=0,1,2, \ldots
$$
We write this as $X \sim \operatorname{Pois}(\lambda)$.
This is a valid PMF because of the Taylor series $\sum_{k=0}^{\infty} \frac{\lambda^{k}}{k !}=e^{\lambda} .$
Example 4.7.2 (Poisson expectation and variance). Let $X \sim \operatorname{Pois}(\lambda)$. We will show that the mean and variance are both equal to $\lambda$. For the mean, we have
$$
\begin{aligned}
E(X) &=e^{-\lambda} \sum_{k=0}^{\infty} k \frac{\lambda^{k}}{k !} \
&=e^{-\lambda} \sum_{k=1}^{\infty} k \frac{\lambda^{k}}{k !} \
&=\lambda e^{-\lambda} \sum_{k=1}^{\infty} \frac{\lambda^{k-1}}{(k-1) !} \
&=\lambda e^{-\lambda} e^{\lambda}=\lambda
\end{aligned}
$$
First we dropped the $k=0$ term because it was 0 . Then we took a $\lambda$ out of the sum so that what was left inside was just the Taylor series for $e^{\lambda}$.
To get the variance, we first find $E\left(X^{2}\right)$. By LOTUS,
$$
E\left(X^{2}\right)=\sum_{k=0}^{\infty} k^{2} P(X=k)=e^{-\lambda} \sum_{k=0}^{\infty} k^{2} \frac{\lambda^{k}}{k !}
$$
From here, the derivation is very similar to that of the variance of the Geometric. Differentiate the familiar series
$$
\sum_{k=0}^{\infty} \frac{\lambda^{k}}{k !}=e^{\lambda}
$$
with respect to $\lambda$ and replenish:
$$
\begin{array}{r}
\sum_{k=1}^{\infty} k \frac{\lambda^{k-1}}{k !}=e^{\lambda}, \
\sum_{k=1}^{\infty} k \frac{\lambda^{k}}{k !}=\lambda e^{\lambda} .
\end{array}
$$
Rinse and repeat:
$$
\begin{aligned}
&\sum_{k=1}^{\infty} k^{2} \frac{\lambda^{k-1}}{k !}=e^{\lambda}+\lambda e^{\lambda}=e^{\lambda}(1+\lambda) \
&\sum_{k=1}^{\infty} k^{2} \frac{\lambda^{k}}{k !}=e^{\lambda} \lambda(1+\lambda)
\end{aligned}
$$
176
Finally,
$$
E\left(X^{2}\right)=e^{-\lambda} \sum_{k=0}^{\infty} k^{2} \frac{\lambda^{k}}{k !}=e^{-\lambda} e^{\lambda} \lambda(1+\lambda)=\lambda(1+\lambda)
$$
so
$$
\operatorname{Var}(X)=E\left(X^{2}\right)-(E X)^{2}=\lambda(1+\lambda)-\lambda^{2}=\lambda
$$
Thus, the mean and variance of a Pois $(\lambda)$ r.v, are both equal to $\lambda$.
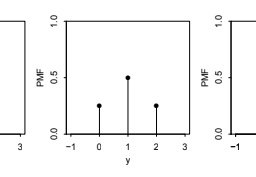
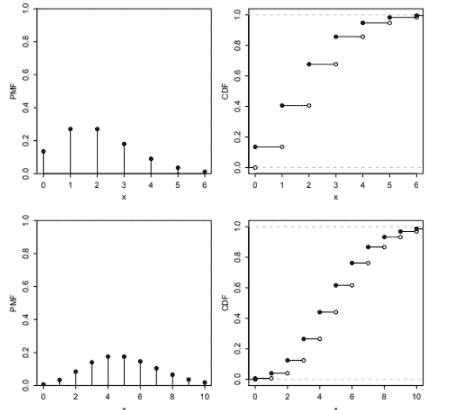
Figure $4.7$ shows the PMF and CDF of the Pois(2) and Pois(5) distributions from $k=0$ to $k=10$. It appears that the mean of the Pois(2) is around 2 and the mean of the Pois $(5)$ is around 5, consistent with our findings above. The PMF of the Pois(2) is highly skewed, but as $\lambda$ grows larger, the skewness is reduced and the PMF becomes more bell-shaped.
统计代考
4.7 泊松
我们将在本章中介绍的最后一个离散分布是 Poisson,它是一种非常流行的离散数据建模分布。我们将介绍它的 PMF、均值和方差,然后更详细地讨论它的故事。
期待
175
定义 4.7.1(泊松分布)。房车$X$ 具有参数 $\lambda$ 的泊松分布,其中 $\lambda>0$,如果 $X$ 的 PMF 为
$$
P(X=k)=\frac{e^{-\lambda} \lambda^{k}}{k !}, \quad k=0,1,2, \ldots
$$
我们把它写成 $X \sim \operatorname{Pois}(\lambda)$。
这是一个有效的 PMF,因为泰勒级数 $\sum_{k=0}^{\infty} \frac{\lambda^{k}}{k !}=e^{\lambda} .$
示例 4.7.2(泊松期望和方差)。设 $X \sim \operatorname{Pois}(\lambda)$。我们将证明均值和方差都等于 $\lambda$。平均而言,我们有
$$
\开始{对齐}
E(X) &=e^{-\lambda} \sum_{k=0}^{\infty} k \frac{\lambda^{k}}{k !} \
&=e^{-\lambda} \sum_{k=1}^{\infty} k \frac{\lambda^{k}}{k !} \
&=\lambda e^{-\lambda} \sum_{k=1}^{\infty} \frac{\lambda^{k-1}}{(k-1) !} \
&=\lambda e^{-\lambda} e^{\lambda}=\lambda
\end{对齐}
$$
首先,我们删除了 $k=0$ 项,因为它是 0 。然后我们从总和中取出 $\lambda$,这样剩下的就是 $e^{\lambda}$ 的泰勒级数。
为了得到方差,我们首先找到$E\left(X^{2}\right)$。通过莲花,
$$
E\left(X^{2}\right)=\sum_{k=0}^{\infty} k^{2} P(X=k)=e^{-\lambda} \sum_{k=0 }^{\infty} k^{2} \frac{\lambda^{k}}{k !}
$$
从这里,推导与几何方差的推导非常相似。区分熟悉的系列
$$
\sum_{k=0}^{\infty} \frac{\lambda^{k}}{k !}=e^{\lambda}
$$
关于 $\lambda$ 并补充:
$$
\开始{数组}{r}
\sum_{k=1}^{\infty} k \frac{\lambda^{k-1}}{k !}=e^{\lambda}, \
\sum_{k=1}^{\infty} k \frac{\lambda^{k}}{k !}=\lambda e^{\lambda} 。
\结束{数组}
$$
冲洗并重复:
$$
\开始{对齐}
&\sum_{k=1}^{\infty} k^{2} \frac{\lambda^{k-1}}{k !}=e^{\lambda}+\lambda e^{\lambda} =e^{\lambda}(1+\lambda) \
&\sum_{k=1}^{\infty} k^{2} \frac{\lambda^{k}}{k !}=e^{\lambda} \lambda(1+\lambda)
\end{对齐}
$$
176
最后,
$$
E\left(X^{2}\right)=e^{-\lambda} \sum_{k=0}^{\infty} k^{2} \frac{\lambda^{k}}{k ! }=e^{-\lambda} e^{\lambda} \lambda(1+\lambda)=\lambda(1+\lambda)
$$
所以
$$
\operatorname{Var}(X)=E\left(X^{2}\right)-(E X)^{2}=\lambda(1+\lambda)-\lambda^{2}=\lambda
$$
因此,Pois $(\lambda)$ r.v 的均值和方差都等于 $\lambda$。
图 $4.7$ 显示了从 $k=0$ 到 $k=10$ 的 Pois(2) 和 Pois(5) 分布的 PMF 和 CDF。 Pois(2) 的平均值似乎在 2 左右,Pois $(5)$ 的平均值在 5 左右,这与我们上面的发现一致。 Pois(2) 的 PMF 高度偏斜,但随着 $\lambda$ 变大,偏斜度减小,PMF 变得更加钟形。
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。