统计代写|Sample spaces and Pebble World stat 代写
统计代考
The mathematical framework for probability is built around sets. Imagine that an experiment is performed, resulting in one out of a set of possible outcomes. Before the experiment is performed, it is unknown which outcome will be the result; after, the result “crystallizes” into the actual outcome.
Definition 1.2.1 (Sample space and event). The sample space $S$ of an experiment is the set of all possible outcomes of the experiment. An event $A$ is a subset of the sample space $S$, and we say that $A$ occurred if the actual outcome is in $A$.
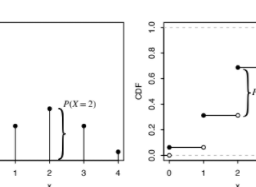
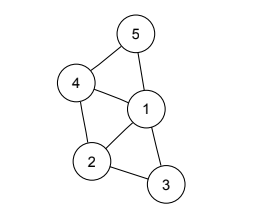
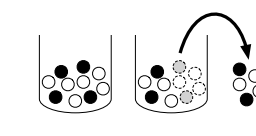
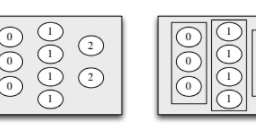
The sample space of an experiment can be finite, countably infinite, or uncountably infinite (see Section A.1.5 of the math appendix for an explanation of countable and uncountable sets). When the sample space is finite, we can visualize it as Pebble World, as shown in Figure 1.1. Each pebble represents an outcome, and an event is a set of pebbles.
Performing the experiment amounts to randomly selecting one pebble. If all the pebbles are of the same mass, all the pebbles are equally likely to be chosen. This special case is the topic of the next two sections. In Section $1.6$, we give a general definition of probability that allows the pebbles to differ in mass.
Set theory is very useful in probability, since it provides a rich language for express-ing and working with events; Section A.1 of the math appendix provides a review of set theory. Set operations, especially unions, intersections, and complements, make it easy to build new events in terms of already-defined events. These concepts also let us express an event in more than one way; often, one expression for an event is much easier to work with than another expression for the same event.
For example, let $S$ be the sample space of an experiment and let $A, B \subseteq S$ be events. Then the union $A \cup B$ is the event that occurs if and only if at least one of $A, B$ occurs, the intersection $A \cap B$ is the event that occurs if and only if both $A$ and $B$ occur, and the complement $A^{c}$ is the event that occurs if and only if $A$ does not occur. We also have $D e$ Morgan’s laws:
$$
(A \cup B)^{c}=A^{c} \cap B^{c} \text { and }(A \cap B)^{c}=A^{c} \cup B^{c},
$$
since saying that it is not the case that at least one of $A$ and $B$ occur is the same as saying that $A$ does not occur and $B$ does not occur, and saying that it is not the case that both occur is the same as saying that at least one does not occur. Analogous results hold for unions and intersections of more than two events.
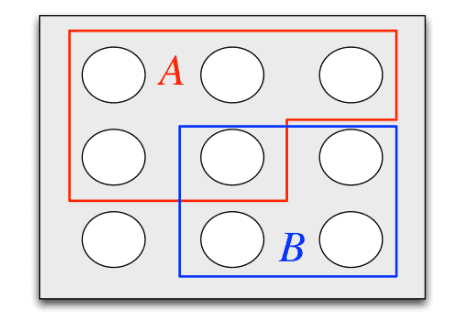
In the example shown in Figure 1.1, $A$ is a set of 5 pebbles, $B$ is a set of 4 pebbles, $A \cup B$ consists of the 8 pebbles in $A$ or $B$ (including the pebble that is in both), $A \cap B$ consists of the pebble that is in both $A$ and $B$, and $A^{c}$ consists of the 4 pebbles that are not in $A$.
The notion of sample space is very general and abstract, so it is important to have some concrete examples in mind.
Example 1.2.2 (Coin flips). A coin is flipped 10 times. Writing Heads as $H$ and Tails as $T$, a possible outcome (pebble) is HHHTHHTTHT, and the sample space is the set of all possible strings of length 10 of $H$ ‘s and $T$ ‘s. We can (and will) encode $H$ as 1 and $T$ as 0 , so that an outcome is a sequence $\left(s_{1}, \ldots, s_{10}\right)$ with $s_{j} \in{0,1}$, and the sample space is the set of all such sequences. Now let’s look at some events:
- Let $A_{1}$ be the event that the first flip is Heads. As a set,
$$
A_{1}=\left{\left(1, s_{2}, \ldots, s_{10}\right): s_{j} \in{0,1} \text { for } 2 \leq j \leq 10\right}
$$
This is a subset of the sample space, so it is indeed an event; saying that $A_{1}$ occurs is the same thing as saying that the first flip is Heads. Similarly, let $A_{j}$ be the event that the $j$ th flip is Heads for $j=2,3, \ldots, 10$. - Let $B$ be the event that at least one flip was Heads. As a set,
$$
B=\bigcup_{j=1}^{10} A_{j} .
$$ - Let $C$ be the event that all the flips were Heads. As a set,4. Let $D$ be the event that there were at least two consecutive Heads. As a set,
$$
D=\bigcup_{j=1}^{9}\left(A_{j} \cap A_{j+1}\right)
$$
Example 1.2.3 (Pick a card, any card). Pick a card from a standard deck of 52 cards. The sample space $S$ is the set of all 52 cards (so there are 52 pebbles, one for each card). Consider the following four events:
- A: card is an ace.
- B: card has a black suit.
- $D$ : card is a diamond.
- $H$ : card is a heart.
As a set, $H$ consists of 13 cards:
{Ace of Hearts, Two of Hearts, …, King of Hearts $}$.
We can create various other events in terms of the events $A, B, D$, and $H$. Unions, intersections, and complements are especially useful for this. For example: - $A \cap H$ is the event that the card is the Ace of Hearts.
- $A \cap B$ is the event {Ace of Spades, Ace of Clubs $} .$
- $A \cup D \cup H$ is the event that the card is red or an ace.
- $(A \cup B)^{c}=A^{c} \cap B^{c}$ is the event that the card is a red non-ace.
Also, note that $(D \cup H)^{c}=D^{c} \cap H^{c}=B$, so $B$ can be expressed in terms of $D$ and $H$. On the other hand, the event that the card is a spade can’t be written in terms of $A, B, D, H$ since none of them are fine-grained enough to be able to distinguish between spades and clubs.
There are many other events that could be defined using this sample space. In fact, the counting methods introduced later in this chapter show that there are $2^{52} \approx 4.5 \times 10^{15}$ events in this problem, even though there are only 52 pebbles.
What if the card drawn were a joker? That would indicate that we had the wrong sample space; we are assuming that the outcome of the experiment is guaranteed to be an element of $S$.
As the preceding examples demonstrate, events can be described in English or in set notation. Sometimes the English description is easier to interpret while the set notation is easier to manipulate. Let $S$ be a sample space and $s_{\text {actual }}$ be the actual outcome of the experiment (the pebble that ends up getting chosen when the experiment is performed). A mini-dictionary for converting between English and sets is given on the next page.
统计代考
概率的数学框架是围绕集合建立的。想象一下,进行了一项实验,产生了一组可能的结果中的一个。在进行实验之前,不知道会是什么结果;之后,结果“结晶”成实际结果。
定义 1.2.1(样本空间和事件)。实验的样本空间 $S$ 是实验所有可能结果的集合。事件 $A$ 是样本空间 $S$ 的子集,如果实际结果在 $A$ 中,我们说 $A$ 发生。
实验的样本空间可以是有限的、可数无限的或不可数无限的(有关可数和不可数集的解释,请参见数学附录的 A.1.5 节)。当样本空间有限时,我们可以将其可视化为 Pebble World,如图 1.1 所示。每个卵石代表一个结果,一个事件是一组卵石。
进行实验相当于随机选择一颗鹅卵石。如果所有小石子的质量相同,那么所有小石子被选中的可能性相同。这种特殊情况是接下来两节的主题。在第 1.6 节中,我们给出了允许卵石质量不同的概率的一般定义。
集合论在概率方面非常有用,因为它为表达和处理事件提供了丰富的语言;数学附录的 A.1 节对集合论进行了回顾。集合操作,尤其是并集、交集和补集,可以很容易地根据已定义的事件构建新事件。这些概念也让我们以不止一种方式表达一个事件;通常,一个事件的一个表达式比同一事件的另一个表达式更容易使用。
例如,令$S$ 为实验的样本空间,令$A, B \subseteq S$ 为事件。那么并集 $A\cup B$ 是当且仅当 $A、B$ 中的至少一个发生时发生的事件,交集 $A\cap B$ 是当且仅当 $A$ 两者都发生时发生的事件和 $B$ 发生,补码 $A^{c}$ 是当且仅当 $A$ 不发生时发生的事件。我们还有 $D e$ Morgan 定律:
$$
(A \cup B)^{c}=A^{c} \cap B^{c} \text { 和}(A \cap B)^{c}=A^{c} \cup B^{c },
$$
因为说 $A$ 和 $B$ 中的至少一个不是发生的情况与说 $A$ 不发生和 $B$ 不发生是相同的,并且说不是这种情况两者都发生与说至少一个不发生是一样的。类似的结果适用于两个以上事件的并集和交集。
在图 1.1 所示的示例中,$A$ 是一组 5 颗鹅卵石,$B$ 是一组 4 颗鹅卵石,$A \cup B$ 由 $A$ 或 $B$ 中的 8 颗鹅卵石组成(包括卵石),$A \cap B$ 由 $A$ 和 $B$ 中的卵石组成,$A^{c}$ 由不在 $A$ 中的 4 个卵石组成。
样本空间的概念非常笼统和抽象,因此记住一些具体的例子很重要。
示例 1.2.2(硬币翻转)。一枚硬币被翻转 10 次。将 Heads 写为 $H$,Tails 写为 $T$,可能的结果(卵石)是 HHHTHHTTHT,样本空间是 $H$ 和 $T$ 的所有可能长度为 10 的字符串的集合。我们可以(并且将)将 $H$ 编码为 1 并将 $T$ 编码为 0 ,因此结果是带有 $s_{ 的序列 $\left(s_{1}, \ldots, s_{10}\right)$ j} \in{0,1}$,样本空间是所有此类序列的集合。现在让我们看一些事件:
- 让 $A_{1}$ 成为第一次翻转是正面的事件。作为一套,
$$
A_{1}=\left{\left(1, s_{2}, \ldots, s_{10}\right): s_{j} \in{0,1} \text { for } 2 \列克 j \列克 10\右}
$$
这是样本空间的一个子集,所以它确实是一个事件;说 $A_{1}$ 发生与说第一个翻转是正面是一样的。类似地,假设 $A_{j}$ 是第 $j$ 次翻转是正面 $j=2,3, \ldots, 10$ 的事件。 - 假设 $B$ 是至少一次翻转是正面的事件。作为一套,
$$
B=\bigcup_{j=1}^{10} A_{j} 。
$$ - 假设 $C$ 是所有翻转都是正面的事件。作为一组,4。假设 $D$ 是至少有两个连续正面的事件。作为一套,
$$
D=\bigcup_{j=1}^{9}\left(A_{j} \cap A_{j+1}\right)
$$
例 1.2.3(选一张牌,任意一张牌)。从一副标准的 52 张牌中挑选一张牌。样本空间 $S$ 是所有 52 张卡片的集合(因此有 52 个鹅卵石,每张卡片一个)。考虑以下四个事件:
- 答:卡是王牌。
- B:卡有黑色西装。
- $D$:卡是钻石。
- $H$:卡片是一颗心。
作为一组,$H$ 由 13 张牌组成:
{红心王牌,红心二,…,红心王$}$。
我们可以根据事件 $A、B、D$ 和 $H$ 创建各种其他事件。并集、交集和补集对此特别有用。例如: - $A \cap H$ 是卡片是红桃 A 的事件。
- $A \cap B$ 是事件 {黑桃 A,梅花 A $} .$
- $A \cup D \cup H$ 是牌是红色或 A 的事件。
- $(A \cup B)^{c}=A^{c} \cap B^{c}$ 是卡片是红色非 A 的事件。
另外,请注意 t
帽子$(D \cup H)^{c}=D^{c} \cap H^{c}=B$,所以$B$可以用$D$和$H$来表示。另一方面,卡片是黑桃的事件不能用$A、B、D、H$来写,因为它们都没有足够细的粒度来区分黑桃和梅花。
可以使用此样本空间定义许多其他事件。事实上,本章后面介绍的计数方法表明,尽管只有 52 颗鹅卵石,但该问题中有 $2^{52} \约 4.5 \times 10^{15}$ 个事件。
如果抽的牌是小丑怎么办?这表明我们有错误的样本空间;我们假设实验的结果保证是$S$的一个元素。
正如前面的例子所展示的,事件可以用英语或集合符号来描述。有时英文描述更容易解释,而集合符号更容易操作。令 $S$ 为样本空间,$s_{\text {actual }}$ 为实验的实际结果(实验执行时最终被选中的小石子)。下一页提供了用于在英语和集合之间进行转换的迷你词典。
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。