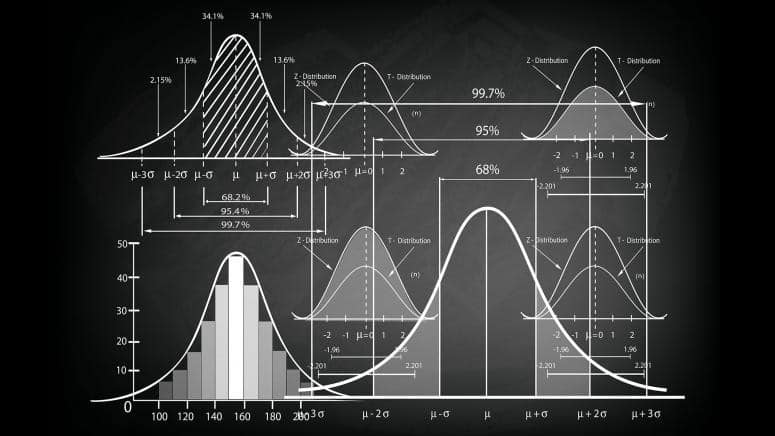
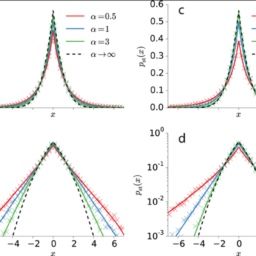
统计代写|Why study probability? stat 代写
Mathematics is the logic of certainty; probability is the logic of uncertainty. Probability is extremely useful in a wide variety of fields, since it provides tools for understanding and explaining variation, separating signal from noise, and modeling complex phenomena. To give just a small sample from a continually growing list of applications:
- Statistics: Probability is the foundation and language for statistics, enabling many powerful methods for using data to learn about the world.
- Physics: Einstein famously said “God does not play dice with the universe”, but current understanding of quantum physics heavily involves probability at the most fundamental level of nature. Statistical mechanics is another major branch of physics that is built on probability.
- Biology: Genetics is deeply intertwined with probability, both in the inheritance of genes and in modeling random mutations.
- Computer science: Randomized algorithms make random choices while they are run, and in many important applications they are simpler and more efficient than any currently known deterministic alternatives. Probability also plays an essential role in studying the performance of algorithms, and in machine learning and artificial intelligence.
- Meteorology: Weather forecasts are (or should be) computed and expressed in terms of probability.
- Gambling: Many of the earliest investigations of probability were aimed at answering questions about gambling and games of chance.
- Finance: At the risk of redundancy with the previous example, it should be pointed out that probability is central in quantitative finance. Modeling stock prices over time and determining “fair” prices for financial instruments are based heavily on probability.
- Political science: In recent years, political science has become more and more quantitative and statistical, with applications such as analyzing surveys of public opinion, assessing gerrymandering, and predicting elections.
- Medicine: The development of randomized clinical trials, in which patients are randomly assigned to receive treatment or placebo, has transformed medical research in recent years. As the biostatistician David Harrington remarked, “Some have conjectured that it could be the most significant advance in scientific medicine in the twentieth century…. In one of the delightful ironies of modern science, the randomized trial ‘adjusts’ for both observed and unobserved heterogeneity in a controlled experiment by introducing chance variation into the study design.” $[16]$
- Life: Life is uncertain, and probability is the logic of uncertainty. While it isn’t practical to carry out a formal probability calculation for every decision made in life, thinking hard about probability can help us avert some common fallacies, shed light on coincidences, and make better predictions.
Probability provides procedures for principled problem-solving, but it can also produce pitfalls and paradoxes. For example, we’ll see in this chapter that even Gottfried Wilhelm von Leibniz and Sir Isaac Newton, the two people who independently discovered calculus in the 17 th century, were not immune to basic errors in probability. Throughout this book, we will use the following strategies to help avoid potential pitfalls.
- Simulation: A beautiful aspect of probability is that it is often possible to study problems via simulation. Rather than endlessly debating an answer with someone who disagrees with you, you can run a simulation and see empirically who is right. Each chapter in this book ends with a section that gives examples of how to do calculations and simulations in $R$, a free statistical computing environment.
- Biohazards: Studying common mistakes is important for gaining a stronger understanding of what is and is not valid reasoning in probability. In this book, common mistakes are called biohazards and are denoted by (since making such mistakes can be hazardous to one’s health!).
Probability and counting
3 - Sanity checks: After solving a problem one way, we will often try to solve the same problem in a different way or to examine whether our answer makes sense in simple and extreme cases.
统计代考
数学是确定性的逻辑;概率是不确定性的逻辑。概率在各种领域都非常有用,因为它提供了用于理解和解释变化、将信号与噪声分离以及对复杂现象建模的工具。从不断增长的应用程序列表中仅提供一小部分示例:
- 统计学:概率是统计学的基础和语言,使许多强大的方法能够利用数据了解世界。
2.物理学:爱因斯坦有句名言“上帝不与宇宙掷骰子”,但目前对量子物理学的理解在很大程度上涉及自然界最基本层面的概率。统计力学是物理学的另一个主要分支,它建立在概率之上。 - 生物学:遗传学与概率密切相关,无论是在基因的遗传中还是在随机突变的建模中。
- 计算机科学:随机算法在运行时做出随机选择,在许多重要应用中,它们比任何当前已知的确定性替代方案更简单、更有效。概率在研究算法性能、机器学习和人工智能方面也起着至关重要的作用。
- 气象学:天气预报是(或应该)用概率计算和表达的。
- 赌博:许多最早的概率调查旨在回答有关赌博和机会游戏的问题。
- 金融:冒着与前面的例子重复的风险,应该指出概率是量化金融的核心。随着时间的推移对股票价格进行建模并确定金融工具的“公平”价格很大程度上基于概率。
- 政治学:近年来,政治学越来越量化和统计化,应用于分析民意调查、评估选区划分、预测选举等。
- 医学:随机临床试验的发展,其中患者被随机分配接受治疗或安慰剂,近年来已经改变了医学研究。正如生物统计学家大卫哈灵顿所说:“有人猜测这可能是 20 世纪科学医学最重大的进步……现代科学令人愉快的讽刺之一是,随机试验对观察到的和通过在研究设计中引入机会变异,在对照实验中未观察到异质性。” $[16]$
10、生命:生命是不确定的,概率是不确定的逻辑。虽然对生活中的每一个决定进行正式的概率计算是不切实际的,但认真思考概率可以帮助我们避免一些常见的谬误,阐明巧合,并做出更好的预测。
概率为有原则的问题解决提供了程序,但它也可能产生陷阱和悖论。例如,我们将在本章中看到,即使是戈特弗里德·威廉·冯·莱布尼茨和艾萨克·牛顿爵士这两位在 17 世纪独立发现微积分的人,也不能幸免于概率的基本错误。在本书中,我们将使用以下策略来帮助避免潜在的陷阱。
- 模拟:概率的一个美丽方面是,通常可以通过模拟来研究问题。与其与不同意你的人无休止地争论答案,你可以运行一个模拟并凭经验看看谁是对的。本书的每一章最后都有一节给出了如何在免费的统计计算环境 $R$ 中进行计算和模拟的示例。
- 生物危害:研究常见错误对于更好地理解什么是有效的概率推理和无效的推理非常重要。在本书中,常见的错误被称为生物危害,并用(因为犯下这样的错误可能会危害一个人的健康!)。
概率和计数
3 - 理智检查:在以一种方式解决问题后,我们经常会尝试以不同的方式解决相同的问题,或者检查我们的答案在简单和极端的情况下是否有意义。

统计代写|Why study probability? stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。