统计代写| Markov property and transition matrix stat代写
统计代考
11.1 Markov property and transition matrix
Markov chains “live” in both space and time: the set of possible values of the $X_{n}$ is called the state space, and the index $n$ represents the evolution of the process over time. The state space of a Markov chain can be either discrete or continuous, and time can also be either discrete or continuous (in the continuous-time setting, we would imagine a process $X_{t}$ defined for all real $t \geq 0$ ). In this chapter we will focus Specifically, we will assume that the $X_{n}$ take values in a finite set, which we usually take to be ${1,2, \ldots, M}$ or ${0,1, \ldots, M}$.
Definition 11.1.1 (Markov chain). A sequence of random variables $X_{0}, X_{1}, X_{2}, \ldots$ taking values in the state space ${1,2, \ldots, M}$ is called a Markov chain if for all $n \geq 0$,
$$
P\left(X_{n+1}=j \mid X_{n}=i, X_{n-1}=i_{n-1}, \ldots, X_{0}=i_{0}\right)=P\left(X_{n+1}=j \mid X_{n}=i\right) .
$$
497
498
The quantity $P\left(X_{n+1}=j \mid X_{n}=i\right)$ is called the transition probability from state $i$ to state $j$. In this book, when referring to a Markov chain we will implicitly assume that it is time-homogeneous, which means that the transition probability $P\left(X_{n+1}=j \mid X_{n}=i\right)$ is the same for all times $n$. But care is needed, since the literature is not consistent about whether to say “time-homogeneous Markov chain” or just “Markov chain”.
The above condition is called the Markov property, and it says that given the entire past history $X_{0}, X_{1}, X_{2}, \ldots, X_{n}$, only the most recent term, $X_{n}$, matters for predicting $X_{n+1}$. If we think of time $n$ as the present, times before $n$ as the past, and times after $n$ as the future, the Markov property says that given the present, the past and future are conditionally independent. The Markov property greatly simplifies computations of conditional probability: instead of having to condition on the entire past, we only need to condition on the most recent value.
To describe the dynamics of a Markov chain, we need to know the probabilities of moving from any state to any other state, that is, the probabilities $P\left(X_{n+1}=\right.$ $j \mid X_{n}=i$ ) on the right-hand side of the Markov property. This information can be encoded in a matrix, called the transition matrix, whose of going from state $i$ to state $j$ in one step of the chain.
Definition 11.1.2 (Transition matrix). Let $X_{0}, X_{1}, X_{2}, \ldots$ be a Markov chain with state space ${1,2, \ldots, M}$, and let $q_{i j}=P\left(X_{n+1}=j \mid X_{n}=i\right.$ ) be the transition probability from state $i$ to state $j$. The $M \times M$ matrix $Q=\left(q_{i j}\right)$ is called the transition matrix of the chain.
Note that $Q$ is a nonnegative matrix in which each row sums to 1 . This is because, starting from any state $i$, the events “move to 1 “, “move to 2 “, …, “move to $M “$ are disjoint, and their union has probability 1 because the chain has to go somewhere.
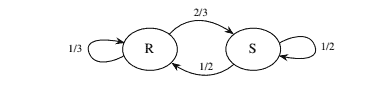
Example 11.1.3 (Rainy-sunny Markov chain). Suppose that on any given day, the weather can either be rainy or sunny. If today is rainy, then tomorrow will be rainy with probability $1 / 3$ and sunny with probability $2 / 3$. If today is sunny, then tomorrow will be rainy with probability $1 / 2$ and sunny with probability $1 / 2$. Letting $X_{n}$ be the weather on day $n, X_{0}, X_{1}, X_{2}, \ldots$ is a Markov chain on the state space ${R, S}$, where $R$ stands for rainy and $S$ for sunny. We know that the Markov prop- erty is satisfied because, from the description of the process, only today’s weather erty is satisfied because, from the matters for predicting tomorrow’s.
The transition matrix of the chain is
$$
\begin{gathered}
R \
R \
S \
\left(\begin{array}{cc}
1 / 3 & 2 / 3 \
1 / 2 & 1 / 2
\end{array}\right)
\end{gathered}
$$
The first row says that starting from state $R$, we transition back to
state $R$ with probability $1 / 3$ and transition to state $S$ with
probability $2 / 3$. The second row says
that starting from state $S$, we have a $1 / 2$ chance of moving to state $R$ and a $1 / 2$ chance of staying in state $S$. We could just as well have used
$$
\begin{gathered}
S \
\left(\begin{array}{cc}
1 / 2 & 1 / 2 \
2 / 3 & 1 / 3
\end{array}\right)
\end{gathered}
$$
as our transition matrix instead. In general, if there isn’t an obvious ordering of the states of a Markov chain (as with the states $R$ and $S$ ), we just need to fix an ordering of the states and use it consistently.
The transition probabilities of a Markov chain can also be represented with a diagram. Each state is represented by a circle, and the arrows indicate the possible one-step transitions; we can imagine a particle wandering around from state to state, randomly choosing which arrow to follow. Next to the arrows we write the corresponding transition probabilities.
What if the weather tomorrow depended on the weather today and the weather yesterday? For example, suppose that the weather behaves as above, except that if there have been two consecutive days of rain, then tomorrow will definitely be sunny, and if there have been two consecutive days of sun, then tomorrow will definitely be rainy. Under these new weather dynamics, the $X_{n}$ no longer form a Markov chain, as the Markov property is violated: conditional on today’s weather, yesterday’s weather can still provide useful information for predicting tomorrow’s weather.
However, by enlarging the state space, we can create a new Markov chain: let $Y_{n}=\left(X_{n-1}, X_{n}\right)$ for $n \geq 1$. Then $Y_{1}, Y_{2}, \ldots$ is a Markov chain on the state space ${(R, R),(R, S),(S, R),(S, S)}$. You can verify that the new transition matrix is
$\left.\begin{array}{l}(R, R) \ (R, R) \ (R, S) \ (S, R) \ (S, S) \ (S, \quad 0 & 1 & 0 & 0 \ 0 & 0 & 1 / 2 & 1 / 2 \ 0 & 0 & 1 & 0\end{array}\right)$
and that its corresponding graphical representation is given in the following figure.
统计代考
11.1 马尔可夫性质和转移矩阵
马尔可夫链“活”在空间和时间上:$X_{n}$ 的可能值集合称为状态空间,索引 $n$ 表示过程随时间的演变。马尔可夫链的状态空间可以是离散的或连续的,时间也可以是离散的或连续的(在连续时间设置中,我们可以想象为所有实数 $t \geq 定义的过程 $X_{t}$ 0 美元)。在本章中,我们将重点关注具体而言,我们将假设 $X_{n}$ 在有限集中取值,我们通常将其取为 ${1,2, \ldots, M}$ 或 ${ 0,1, \ldots, M}$.
定义 11.1.1(马尔可夫链)。在状态空间 ${1,2, \ldots, M}$ 中取值的随机变量序列 $X_{0}, X_{1}, X_{2}, \ldots$ 称为马尔可夫链,如果对于所有 $n \geq 0$,
$$
P\left(X_{n+1}=j \mid X_{n}=i, X_{n-1}=i_{n-1}, \ldots, X_{0}=i_{0}\right) =P\left(X_{n+1}=j \mid X_{n}=i\right) 。
$$
497
498
量 $P\left(X_{n+1}=j \mid X_{n}=i\right)$ 称为从状态 $i$ 到状态 $j$ 的转移概率。在本书中,当提到马尔可夫链时,我们会隐含地假设它是时间齐次的,这意味着转移概率 $P\left(X_{n+1}=j \mid X_{n}=i\right )$ 对于所有时间 $n$ 都是相同的。但是需要注意,因为文献对于是说“时间齐次马尔可夫链”还是仅仅说“马尔可夫链”并不一致。
上述条件称为马尔可夫属性,它表示给定整个过去的历史 $X_{0}, X_{1}, X_{2}, \ldots, X_{n}$,只有最近的术语 $ X_{n}$,对于预测 $X_{n+1}$ 很重要。如果我们将时间 $n$ 视为现在,将 $n$ 之前的时间视为过去,将 $n$ 之后的时间视为未来,马尔可夫性质说,给定现在,过去和未来是条件独立的。马尔可夫属性极大地简化了条件概率的计算:我们不必以整个过去为条件,我们只需要以最近的值为条件。
为了描述马尔可夫链的动力学,我们需要知道从任何状态移动到任何其他状态的概率,即概率 $P\left(X_{n+1}=\right.$ $j \mid X_{n}=i$ ) 在马尔可夫属性的右侧。该信息可以被编码在一个矩阵中,称为转移矩阵,其在链的一个步骤中从状态 $i$ 到状态 $j$。
定义 11.1.2(转移矩阵)。令 $X_{0}, X_{1}, X_{2}, \ldots$ 为状态空间为 ${1,2, \ldots, M}$ 的马尔可夫链,令 $q_{ij}= P\left(X_{n+1}=j \mid X_{n}=i\right.$ ) 是从状态 $i$ 到状态 $j$ 的转移概率。 $M\times M$ 矩阵$Q=\left(q_{i j}\right)$ 称为链的转移矩阵。
请注意,$Q$ 是一个非负矩阵,其中每一行的总和为 1。这是因为,从任何状态 $i$ 开始,事件“移至 1”、“移至 2”、…、“移至 $M”$ 是不相交的,并且它们的并集概率为 1,因为链有去某个地方。
示例 11.1.3(晴雨马尔可夫链)。假设在任何一天,天气可能是下雨或晴天。如果今天下雨,那么明天下雨的概率为 $1 / 3$,晴天的概率为 $2 / 3$。如果今天是晴天,那么明天下雨的概率为 $1 / 2$,晴天的概率为 $1 / 2$。设 $X_{n}$ 为第 $n 天的天气,X_{0}, X_{1}, X_{2},\ldots$ 是状态空间 ${R, S}$ 上的马尔可夫链,其中 $R$ 代表下雨,$S$ 代表晴天。我们知道马尔可夫性质是满足的,因为从过程的描述来看,只有今天的天气条件是满足的,因为从预测明天的事情来看。
链的转移矩阵是
$$
\开始{聚集}
\
\
S \
\left(\begin{数组}{cc}
1 / 3 & 2 / 3 \
1 / 2 & 1 / 2
\end{数组}\右)
\结束{聚集}
$$
第一行表示从状态 $R$ 开始,我们转换回
状态 $R$ 概率为 $1 / 3$ 并转换到状态 $S$
概率 $2 / 3$。第二行说
从状态 $S$ 开始,我们有 $1 / 2$ 的机会移动到状态 $R$ 和 $1 / 2$ 的机会留在状态 $S$。我们也可以使用
$$
\开始{聚集}
S \
\left(\begin{数组}{cc}
1 / 2 & 1 / 2 \
2 / 3 & 1 / 3
\end{数组}\右)
\结束{聚集}
$$
作为我们的转换矩阵。一般来说,如果马尔可夫链的状态没有明显的顺序(如状态 $R$ 和 $S$ ),我们只需要固定状态的顺序并一致地使用它。
马尔可夫链的转移概率也可以用图表来表示。每个状态用一个圆圈表示,箭头表示可能的一步转换;我们可以想象一个粒子从一个状态到另一个状态,随机选择跟随哪个箭头。在箭头旁边,我们写下相应的转移概率。
如果明天的天气取决于今天的天气和昨天的天气怎么办?例如,苏
。
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。