统计代写| Reversibility stat代写
统计代考
11.4 Reversibility
We have seen that the stationary distribution of a Markov chain is extremely useful for understanding its long-run behavior. Unfortunately, in general it may be computationally difficult to find the stationary distribution when the state space is large. This section addresses an important special case where working with eigenvalue equations for large matrices can be avoided.
514
Definition 11.4.1 (Reversibility). Let $Q=\left(q_{i j}\right)$ be the transition matrix of a Markov chain. Suppose there is $\mathrm{s}=\left(s_{1}, \ldots, s_{M}\right)$ with $s_{i} \geq 0, \sum_{i} s_{i}=1$, such that
$$
s_{i} q_{i j}=s_{j} q_{j i}
$$
for all states $i$ and $j$. This equation is called the reversibility or detailed balance condition, and we say that the chain is reversible with respect to $\mathrm{s}$ if it holds.
The term “reversible” comes from the fact that a reversible chain, started according to its stationary distribution, behaves in the same way regardless of whether time is run forwards or backwards. If you record a video of a reversible chain, started according to its stationary distribution, and then show the video to a friend, either in the normal way or with time reversed, your friend will not be able to determine from watching the video whether time is running forwards or backwards.
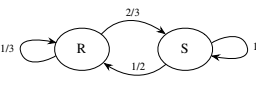
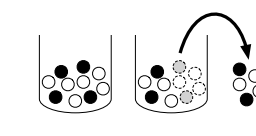
As discussed after Definition 11.3.1, we can think about the stationary distribution of a Markov chain intuitively in terms of a system consisting of a large number of particles independently bouncing around according to the transition probabilities. In the long run, the proportion of particles in any state $j$ is the stationary probability of state $j$, and the flow of particles out of state $j$ is counterbalanced by the flow of sarticles into state $j .$ fo see this in more detail, let $n$ be the number of particles and $j$. By definition, $\mathbf{s}$ is the stationary distribution of the chain if and only if
$$
s_{j}=\sum_{i} s_{i} q_{i j}=s_{j} q_{j j}+\sum_{i: i \neq j} s_{i} q_{i j}
$$
for all states $j$. This equation can be rewritten as
$$
n s_{j}\left(1-q_{j j}\right)=\sum_{i: i \neq j} n s_{i} q_{i j}
$$
The left-hand side is the approximate number of particles that will exit from state $j$ on the next step, since there are $n s_{j}$ particles at state $j$, each of which will stay at $j$ with probability $q_{j j}$ and leave with probability $1-q_{j j} .$ The right-hand side is the approximate number of particles that will enter state $j$ on the next step, since for each $i \neq j$ there are $n s_{i}$ particles at state $i$, each of which will enter state $j$ with probability $q_{i j}$. So there is a balance between particles leaving state $j$ and particles entering state $j$.
The reversibility condition imposes a much more stringent form of balance, in which for each pair of states $i, j$ with $i \neq j$, the flow of particles from state $i$ to state $j$ is counterbalanced by the flow of particles from state $j$ to state $i$. To see this, write the reversibility equation for states $i$ and $j$ as
$$
n s_{i} q_{i j}=n s_{j} q_{j i}
$$
The left-hand side is the approximate number of particles that will go from state $i$ to state $j$ on the next step, since there are $n s_{i}$ particles at state $i$, each of which
统计代考
11.4 可逆性
我们已经看到,马尔可夫链的平稳分布对于理解其长期行为非常有用。不幸的是,一般来说,当状态空间很大时,在计算上可能很难找到平稳分布。本节讨论一个重要的特殊情况,可以避免使用大型矩阵的特征值方程。
514
定义 11.4.1(可逆性)。令$Q=\left(q_{i j}\right)$ 为马尔可夫链的转移矩阵。假设有 $\mathrm{s}=\left(s_{1}, \ldots, s_{M}\right)$ 其中 $s_{i} \geq 0, \sum_{i} s_{i}=1 $,这样
$$
s_{i} q_{i j}=s_{j} q_{j i}
$$
对于所有状态 $i$ 和 $j$。这个方程被称为可逆性或详细平衡条件,如果它成立,我们说链相对于 $\mathrm{s}$ 是可逆的。
“可逆”一词源于这样一个事实,即根据其平稳分布开始的可逆链无论时间是向前还是向后运行,都以相同的方式运行。如果你录制一个可逆链的视频,按照它的平稳分布开始,然后以正常方式或时间倒转的方式将视频显示给朋友,你的朋友将无法通过观看视频来确定时间是否正在向前或向后运行。
正如定义 11.3.1 之后所讨论的,我们可以直观地考虑马尔可夫链的平稳分布,该系统由大量粒子根据转移概率独立弹跳组成的系统。从长远来看,任何状态$j$中的粒子比例是状态$j$的平稳概率,并且离开状态$j$的粒子流被进入状态$j.$的粒子流抵消。更详细地看到这一点,设$n$为粒子数,$j$。根据定义,$\mathbf{s}$ 是链的平稳分布当且仅当
$$
s_{j}=\sum_{i} s_{i} q_{i j}=s_{j} q_{j j}+\sum_{i: i \neq j} s_{i} q_{i j}
$$
对于所有状态 $j$。这个方程可以改写为
$$
n s_{j}\left(1-q_{j j}\right)=\sum_{i: i \neq j} n s_{i} q_{i j}
$$
左边是在下一步退出状态 $j$ 的粒子的近似数量,因为在状态 $j$ 有 $n s_{j}$ 个粒子,每个粒子都将停留在 $j$概率为 $q_{jj}$ 并且以概率 $1-q_{jj} 离开。 j$在状态$i$有$n s_{i}$个粒子,每个粒子都会以$q_{ij}$的概率进入状态$j$。所以在离开状态 $j$ 的粒子和进入状态 $j$ 的粒子之间存在平衡。
可逆性条件强加了一种更严格的平衡形式,其中对于每对状态 $i, j$ 和 $i \neq j$,粒子从状态 $i$ 到状态 $j$ 的流动由从状态 $j$ 到状态 $i$ 的粒子流。要看到这一点,请将状态 $i$ 和 $j$ 的可逆性方程写为
$$
n s_{i} q_{i j}=n s_{j} q_{j i}
$$
左边是在下一步从状态 $i$ 到状态 $j$ 的粒子的近似数量,因为在状态 $i$ 有 $n s_{i}$ 个粒子,每个粒子
R语言代写

统计代写|SAMPLE SPACES AND PEBBLE WORLD stat 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。