数学代写| Integral of interpolant $int_{a}^{b} p_{n} mathrm{~d} x$ approximates $int_{a}^{b} f mathrm{~d} x$ 数值分析代考
数值分析代写
Theorem 3 (Gauss quadrature).
If the interpolation points $\left{x_{i}\right}_{i=0}^{n}$ are chosen to be roots of an orthogonal system of polynomials of degree $n+1$ for a weighted inner product given by the weight function $w(x)$, then
$$
\int_{a}^{b} p_{n}(x) w(x) \mathrm{d} x=\int_{a}^{b} f(x) w(x) \mathrm{d} x
$$
for all $f \in \mathcal{P}_{2 n+1}$
- Without this special choice of points $\left{x_{i}\right}_{i=0}^{n}$ the integral would be exactly only for all $f \in \mathcal{P}_{n}$.
Chebyshev polynomials and Chebyshev points - Let $[a, b]=[-1,1]$.
- Chebysher polynomial of degree $n, T_{n}$ is given by the formula
$$
T_{n}(x)=\cos (n \arccos (x))
$$ - $\left{T_{n}\right}$ form an orthogonal system of polynomials, that is,
$$
\int_{-1}^{1} T_{n}(x) T_{m}(x) w(x) \mathrm{d} x=0, \quad \text { if } n \neq m
$$
where the weight function is $w(x)=\sqrt{1-x^{2}}$. - $T_{n}$ satisfies the recurrence relation
$$
T_{n+1}(x)=2 x T_{n}(x)-T_{n-1}(x)
$$
Chebyshev points
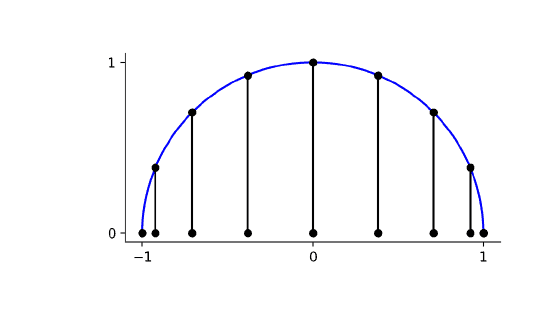
- We shall call the extrema of $T_{n}=\cos (n \arccos (x))$ the chebyshev points,
$$
x_{i}=\cos \left(\frac{i \pi}{n}\right), \quad j=0,1, \ldots, n .
$$ - These points can be viewed as the $x$-coordinates of some equi-distanced points lying on a circle
数值分析代考
定理 3(高斯求积)。
如果插值点 $\left{x_{i}\right}_{i=0}^{n}$ 被选为加权内部的 $n+1$ 次多项式正交系统的根由权重函数 $w(x)$ 给出的乘积,然后
$$
\int_{a}^{b} p_{n}(x) w(x) \mathrm{d} x=\int_{a}^{b} f(x) w(x) \mathrm{d} x
$$
对于所有 $f \in \mathcal{P}_{2 n+1}$
- 如果没有这种特殊的点选择 $\left{x_{i}\right}_{i=0}^{n}$,积分将仅适用于所有 $f \in \mathcal{P}_{ n}$。
切比雪夫多项式和切比雪夫点 - 令 $[a, b]=[-1,1]$。
- 次数 $n, T_{n}$ 的 Chebysher 多项式由公式给出
$$
T_{n}(x)=\cos (n \arccos (x))
$$ - $\left{T_{n}\right}$ 形成一个正交的多项式系统,即,
$$
\int_{-1}^{1} T_{n}(x) T_{m}(x) w(x) \mathrm{d} x=0, \quad \text { if } n \neq m
$$
其中权重函数为 $w(x)=\sqrt{1-x^{2}}$。 - $T_{n}$ 满足递归关系
$$
T_{n+1}(x)=2 x T_{n}(x)-T_{n-1}(x)
$$
切比雪夫点
- 我们将 $T_{n}=\cos (n \arccos (x))$ 的极值称为切比雪夫点,
$$
x_{i}=\cos \left(\frac{i \pi}{n}\right), \quad j=0,1, \ldots, n 。
$$ - 这些点可以看作是位于一个圆上的一些等距离点的$x$-坐标

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程